Rで機械学習:K近傍法

# 再現性のための乱数シード設定
seed <- 20250813
set.seed(seed)

# 1. データ準備
# 意図的に2つのクラスの境界が曖昧なデータセットを生成します。
# (注意) k_value は下記のステップ3の結果を確認した後に決定しています。
n <- 60 # 各クラスのデータ数
attackers <- data.frame(attack_freq = rnorm(n, mean = 18, sd = 5), defense_ratio = rnorm(n, mean = 22, sd = 8))
guardians <- data.frame(attack_freq = rnorm(n, mean = 12, sd = 6), defense_ratio = rnorm(n, mean = 38, sd = 10))
train_data <- rbind(attackers, guardians)
train_labels <- as.factor(c(rep("アタッカー", n), rep("ガーディアン", n)))
new_player <- data.frame(attack_freq = 16, defense_ratio = 30)
k_value <- 9

cat(paste("\n新人プレイヤー(攻撃頻度:", new_player$attack_freq, ", 防御比率:", new_player$defense_ratio, ")のスタイルを予測します。\n"))

# 2. 【距離計算】新人プレイヤーと全プレイヤーの距離を計算
distances <- apply(train_data, 1, function(point) {
  sqrt(sum((point - new_player)^2))
})

# 3. 【近傍点特定】距離が近い順に並べ替え、上位k個のインデックスを取得
sorted_indices <- order(distances)
nearest_indices <- head(sorted_indices, k_value)

# 4. 【多数決】特定した近傍点のラベルを取得して集計
nearest_labels <- train_labels[nearest_indices]
cat(paste0("\n■ 投票結果の集計 (k=", k_value, "の場合):\n"))
print(table(nearest_labels))

# 5. 【予測】多数決で最も多かったクラスを予測結果とする
prediction <- names(which.max(table(nearest_labels)))
cat("\n■ 多数決による最終予測結果:\n")
cat("新人プレイヤーのスタイルは「", prediction, "」と予測されました。\n")

# 6. 【可視化】計算過程をプロットで確認
nearest_neighbors_data <- train_data[nearest_indices, ]
p_knn_manual <- ggplot(as.data.frame(train_data), aes(x = attack_freq, y = defense_ratio)) +
  geom_point(aes(color = train_labels, shape = train_labels), size = 3, alpha = 0.7) +
  geom_point(data = new_player, aes(x = attack_freq, y = defense_ratio), color = "blue", size = 6, shape = 4, stroke = 1.5) +
  geom_point(data = nearest_neighbors_data, shape = 21, size = 5, stroke = 1.5, color = "black") +
  scale_color_manual(values = c("アタッカー" = "red", "ガーディアン" = "darkgreen")) +
  scale_shape_manual(values = c("アタッカー" = 16, "ガーディアン" = 17)) +
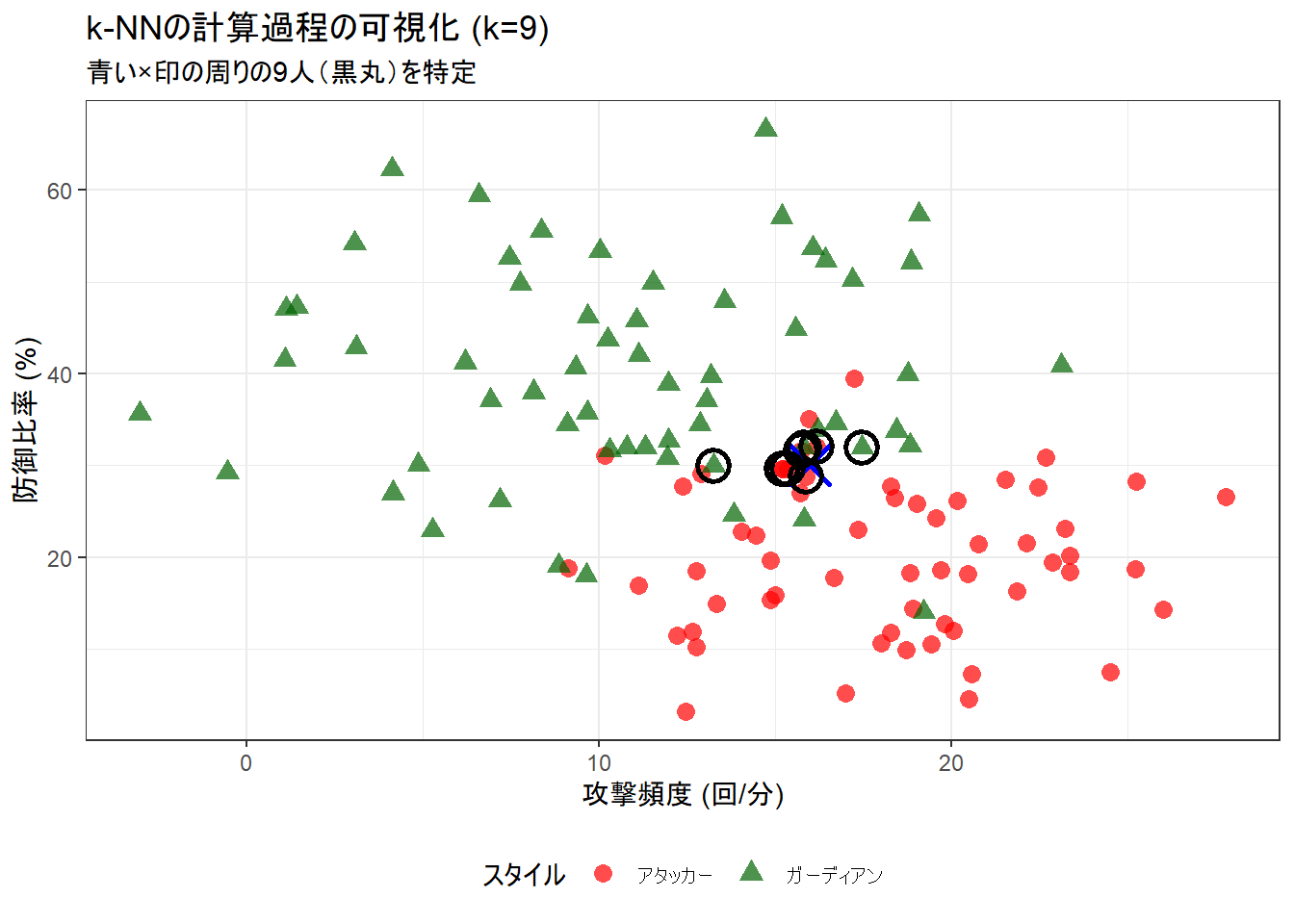
  labs(title = paste0("k-NNの計算過程の可視化 (k=", k_value, ")"), subtitle = paste0("青い×印の周りの", k_value, "人（黒丸）を特定"), x = "攻撃頻度 (回/分)", y = "防御比率 (%)", color = "スタイル", shape = "スタイル") +
  theme_bw() +
  theme(legend.position = "bottom")

print(p_knn_manual)

# kの値を変えた場合に、決定境界がどのように変化するかを比較します。
# グリッドデータ等の準備
grid_range <- apply(train_data, 2, range)
x_grid <- seq(from = grid_range[1, 1], to = grid_range[2, 1], length.out = 150)
y_grid <- seq(from = grid_range[1, 2], to = grid_range[2, 2], length.out = 150)
grid_df_base <- expand.grid(attack_freq = x_grid, defense_ratio = y_grid)
k_list <- c(1, 9, 30)
prediction_list <- list()

for (k in k_list) {
  grid_df_temp <- grid_df_base
  # ここでは簡便さのため、class::knnを使用
  predicted_classes <- knn(train = train_data, test = grid_df_temp[, 1:2], cl = train_labels, k = k)
  grid_df_temp$predicted_class <- predicted_classes
  grid_df_temp$k <- paste("k =", k)
  prediction_list[[paste0("k=", k)]] <- grid_df_temp
}
all_predictions <- bind_rows(prediction_list)

train_df <- as.data.frame(train_data)
train_df$label <- train_labels
train_data_for_plot <- lapply(k_list, function(k_val) {
  mutate(train_df, k = paste("k =", k_val))
}) %>% bind_rows()

# ファセットの順序を制御するために因子型に変換
level_order <- paste("k =", k_list)
all_predictions$k <- factor(all_predictions$k, levels = level_order)
train_data_for_plot$k <- factor(train_data_for_plot$k, levels = level_order)

# プロットの作成
p_boundary <- ggplot() +
  geom_raster(data = all_predictions, aes(x = attack_freq, y = defense_ratio, fill = predicted_class), alpha = 0.3, interpolate = TRUE) +
  geom_point(data = train_data_for_plot, aes(x = attack_freq, y = defense_ratio, color = label), size = 2) +
  facet_wrap(~k) +
  scale_color_manual(name = "実績データ", values = c("アタッカー" = "red", "ガーディアン" = "darkgreen")) +
  scale_fill_manual(name = "予測領域", values = c("アタッカー" = "red", "ガーディアン" = "darkgreen")) +
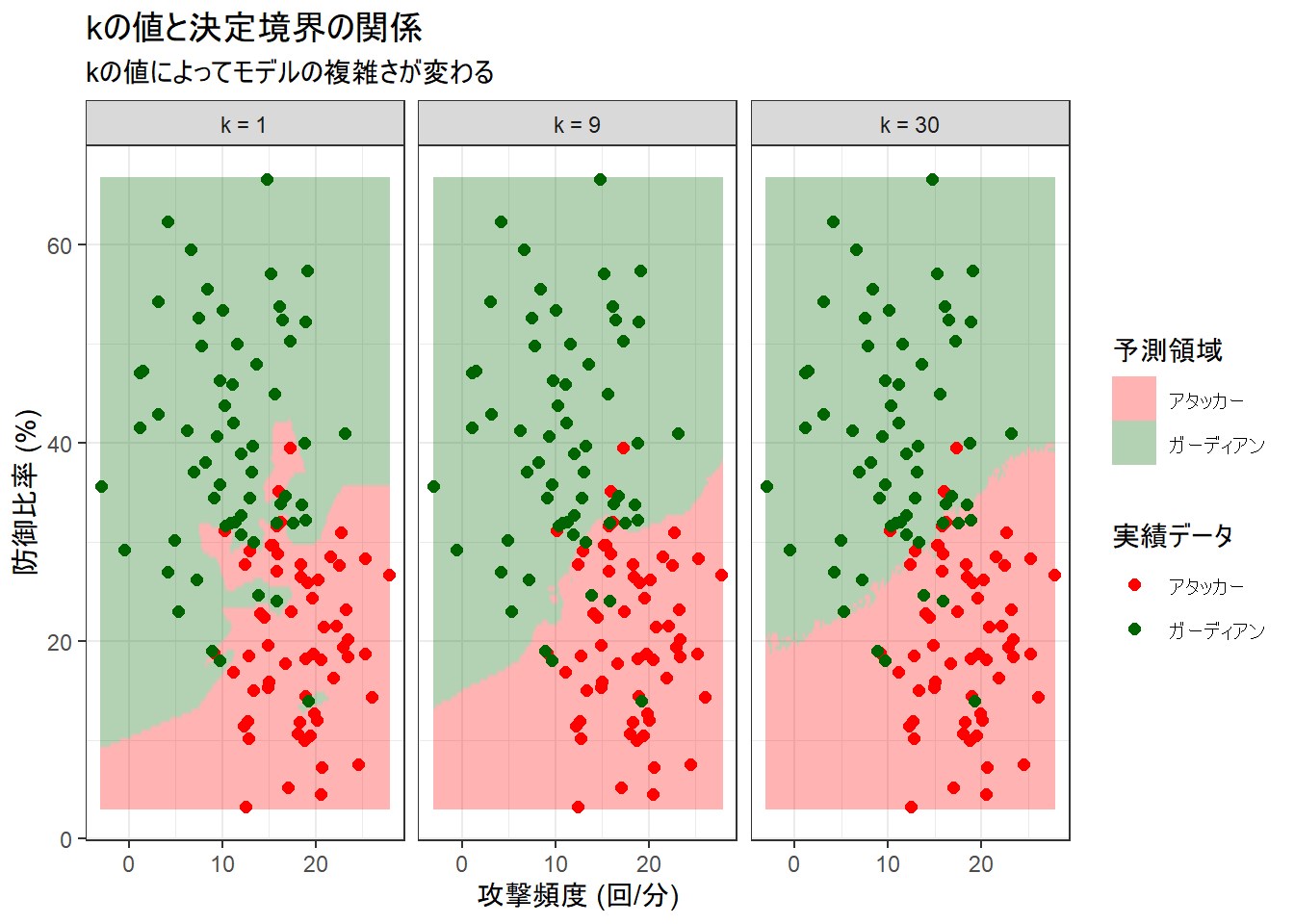
  labs(title = "kの値と決定境界の関係", subtitle = "kの値によってモデルの複雑さが変わる", x = "攻撃頻度 (回/分)", y = "防御比率 (%)") +
  theme_bw()

print(p_boundary)

# 1. データを準備
train_df_for_cv <- as.data.frame(train_data)
train_df_for_cv$label <- train_labels

# 2. クロスバリデーションの設定 (10-fold)
set.seed(seed)
cv_control <- trainControl(method = "cv", number = 10)

# 3. 試したいkの値のリストを作成 (候補を増やす)
k_grid <- expand.grid(k = c(1, 3, 5, 7, 9, 11, 15, 21, 31))

# 4. train関数でモデルの学習とクロスバリデーションを同時に実行
knn_cv_results <- train(
  label ~ .,
  data = train_df_for_cv,
  method = "knn",
  trControl = cv_control,
  tuneGrid = k_grid,
  preProcess = c("center", "scale")
)

# 5. 結果の表示
cat("■ 数量的な評価結果:\n")
print(knn_cv_results)

cat("\n■ 結果をグラフで可視化:\n")
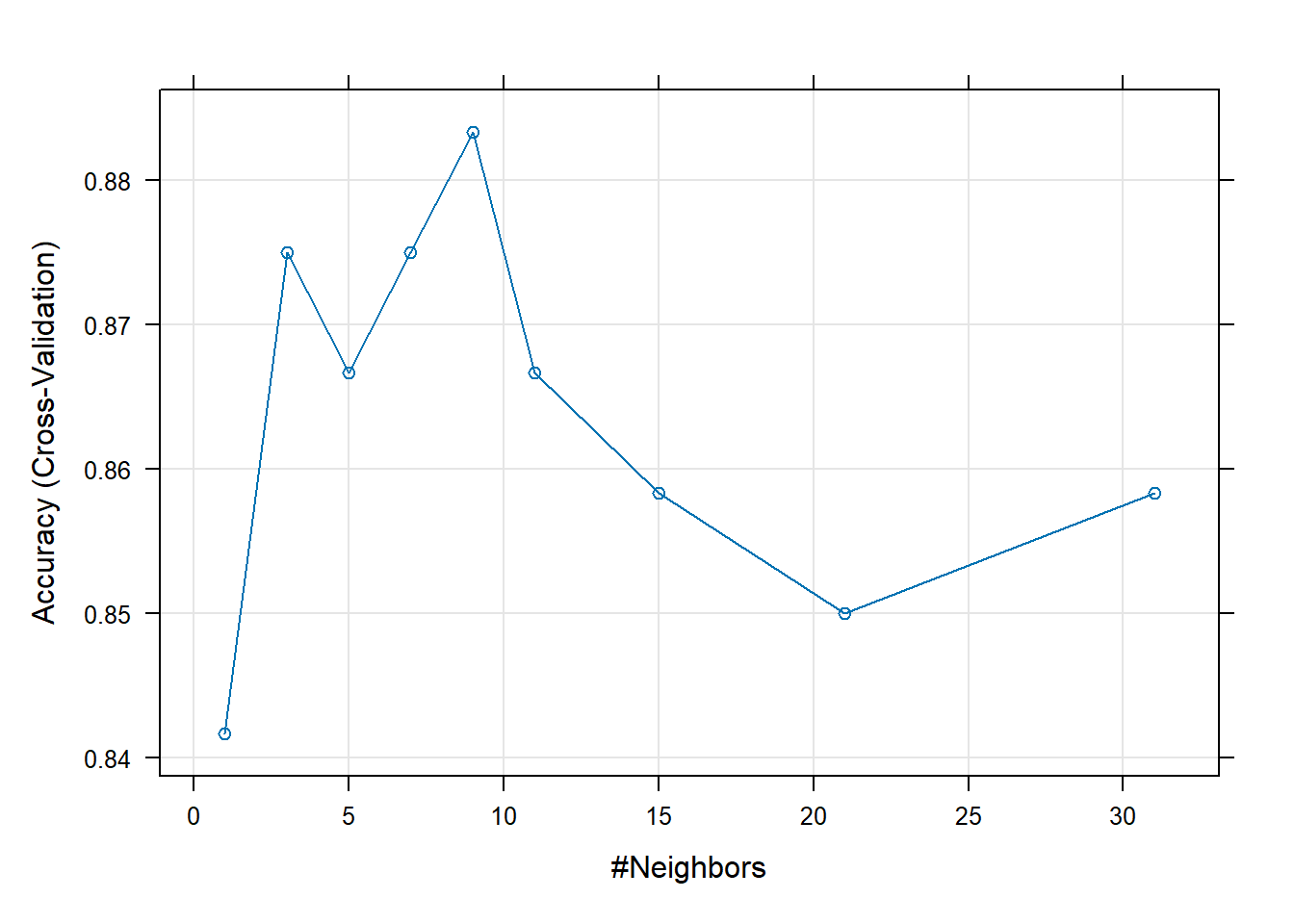
plot(knn_cv_results)