Rで 機械学習:k-means を試みます。
本ポストはこちらの続きです。

1. k-meansとは
k-means は、教師なし学習のクラスタリング手法です。 データを事前に指定したクラスタ数 \(k\) に分け、各クラスタの重心(centroid)と各点の割り当てを繰り返し更新して、クラスタ内のばらつき(誤差平方和, SSE)を最小化します。
基本の流れ
- 初期重心をランダムに設定
- 各データ点を最も近い重心に割り当て
- 各クラスタの平均位置を計算し、重心を更新
- 割り当てが変化しなくなるまで繰り返す
2. シミュレーションのシナリオ
今回は以下のようなサンプルデータを作成します。
- 3つの明確なグループがある2次元データ
- 各クラスタ100点、合計300点
- これをk-meansで解析し、3種類の手法(Elbow, Silhouette, Gap Statistic)で推奨kを求める
3. R言語によるシミュレーションコード
library(ggplot2)
library(cluster)
library(factoextra)
library(gridExtra)
# ---------- Elbow法の推奨k検出(二次多項式フィット) ----------
detect_elbow <- function(sse, k_range) {
fit <- lm(sse ~ poly(k_range, 2, raw = TRUE))
pred <- predict(fit, newdata = data.frame(k_range = k_range))
residuals <- sse - pred
elbow_k <- k_range[which.min(residuals)]
return(elbow_k)
}
# ---------- 推奨kを求めてプロットする関数 ----------
find_optimal_k <- function(data, k_min = 2, k_max = 10, B = 50, seed) {
set.seed(seed)
k_range <- k_min:k_max
# 1. Elbow法(SSE)
sse <- numeric(length(k_range))
for (i in seq_along(k_range)) {
km <- kmeans(data, centers = k_range[i], nstart = 20)
sse[i] <- km$tot.withinss
}
elbow_k <- detect_elbow(sse, k_range)
df_sse <- data.frame(k = k_range, value = sse, method = "SSE (Elbow)")
# 2. シルエット係数
sil <- numeric(length(k_range))
for (i in seq_along(k_range)) {
km <- kmeans(data, centers = k_range[i], nstart = 20)
ss <- silhouette(km$cluster, dist(data))
sil[i] <- mean(ss[, 3])
}
sil_k <- k_range[which.max(sil)]
df_sil <- data.frame(k = k_range, value = sil, method = "Silhouette")
# 3. ギャップ統計量
gap_stat <- clusGap(data, FUN = kmeans, K.max = k_max, B = B, nstart = 20)
gap_values <- gap_stat$Tab[, "gap"]
gap_se <- gap_stat$Tab[, "SE.sim"]
gap_k <- maxSE(f = gap_values, SE.f = gap_se, method = "firstSEmax")
df_gap <- data.frame(k = 1:k_max, value = gap_values, method = "Gap Statistic")
df_gap <- df_gap[df_gap$k %in% k_range, ]
# 4. 評価指標比較グラフ
df_all <- rbind(df_sse, df_sil, df_gap)
plot_metrics <- ggplot(df_all, aes(x = k, y = value, color = method)) +
geom_line() +
geom_point() +
scale_x_continuous(breaks = k_range) +
facet_wrap(~method, scales = "free_y") +
labs(
title = "クラスタ数選択の3手法比較",
x = "クラスタ数 k",
y = "指標値"
) +
theme_minimal()
# 5. クラスタリング前のデータ
plot_original <- ggplot(data, aes(x = x, y = y)) +
geom_point(alpha = 0.7) +
labs(
title = "クラスタリング前のデータ",
x = "X", y = "Y"
) +
theme_minimal()
# 6. 各推奨kでクラスタリング&散布図
make_cluster_plot <- function(k_value, method_name) {
km <- kmeans(data, centers = k_value, nstart = 20)
cluster_df <- data.frame(data, cluster = factor(km$cluster))
ggplot(cluster_df, aes(x = x, y = y, color = cluster)) +
geom_point(size = 2, alpha = 0.7) +
labs(
title = paste(method_name, " 推奨k =", k_value),
x = "X", y = "Y"
) +
theme_minimal() +
scale_color_brewer(palette = "Set1")
}
plot_elbow <- make_cluster_plot(elbow_k, "Elbow法")
plot_sil <- make_cluster_plot(sil_k, "Silhouette法")
plot_gap <- make_cluster_plot(gap_k, "Gap統計量")
# 7. 3つのクラスタリング結果をまとめる
# plot_clusters_all <- grid.arrange(plot_elbow, plot_sil, plot_gap, ncol = 3) では出力される
# プロットをリストにまとめる
plot_clusters_all <- list(plot_elbow, plot_sil, plot_gap)
return(list(
recommended_k = list(
Elbow = elbow_k,
Silhouette = sil_k,
Gap_Statistic = gap_k
),
plot_original = plot_original,
metrics_plot = plot_metrics,
cluster_plots = plot_clusters_all
))
}
# ---------- データ生成 ----------
seed <- 20250814
set.seed(seed)
n <- 100
group1 <- data.frame(
x = rnorm(n, mean = 0, sd = 0.5),
y = rnorm(n, mean = 0, sd = 0.5)
)
group2 <- data.frame(
x = rnorm(n, mean = 3, sd = 0.5),
y = rnorm(n, mean = 0, sd = 0.5)
)
group3 <- data.frame(
x = rnorm(n, mean = 1.5, sd = 0.5),
y = rnorm(n, mean = 2.5, sd = 0.5)
)
data <- rbind(group1, group2, group3)
# ---------- 実行 ----------
result <- find_optimal_k(data, k_min = 2, k_max = 10, B = 50, seed = seed)
# クラスタリング前のデータ
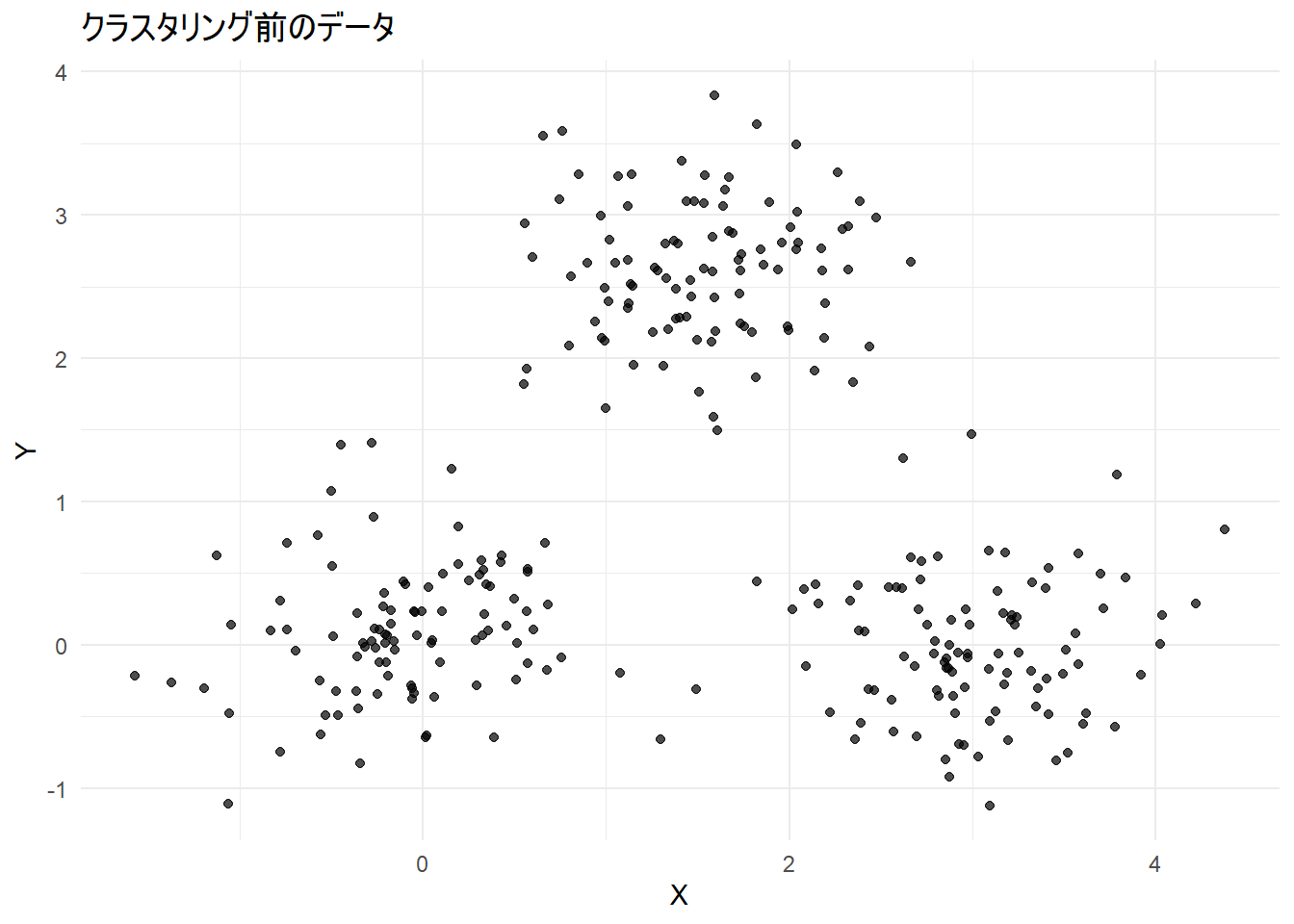
print(result$plot_original)Figure 1 はクラスタリング前のサンプルデータです。
意図的に3つの明確なグループを形成させています。
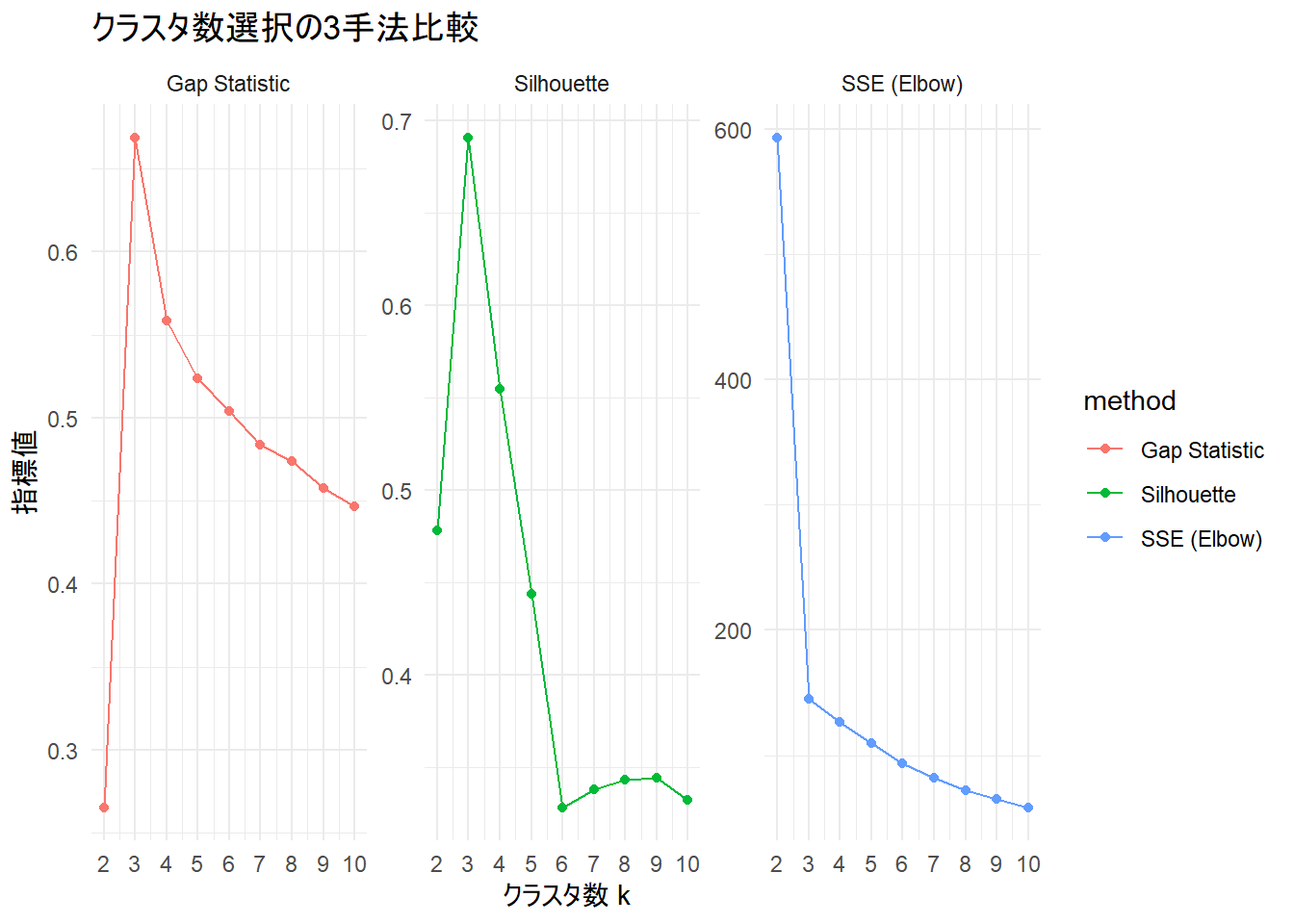
続いてエルボー法、シルエット法、Gap統計量の3つの方法による推奨されるクラスタリング数(k)を確認します。
コードのコンセプトは 4. k-meansにおけるクラスタ数決定 を参照してください。
# 推奨kを出力
print(result$recommended_k)$Elbow
[1] 3
$Silhouette
[1] 3
$Gap_Statistic
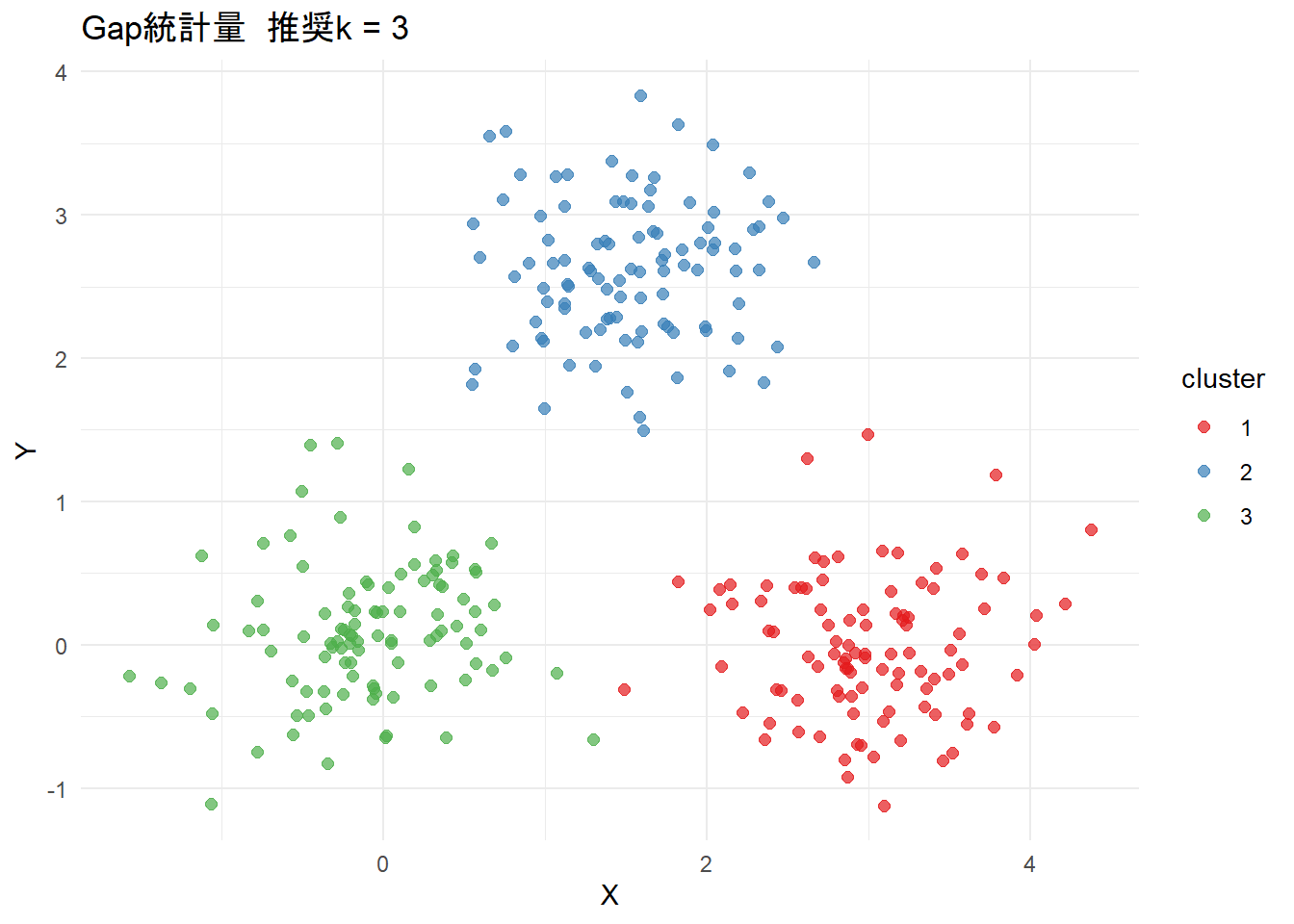
[1] 33つの方法すべてで k=3 が推奨され、シナリオ通りの結果が得られます。
シミュレーション過程を可視化します。
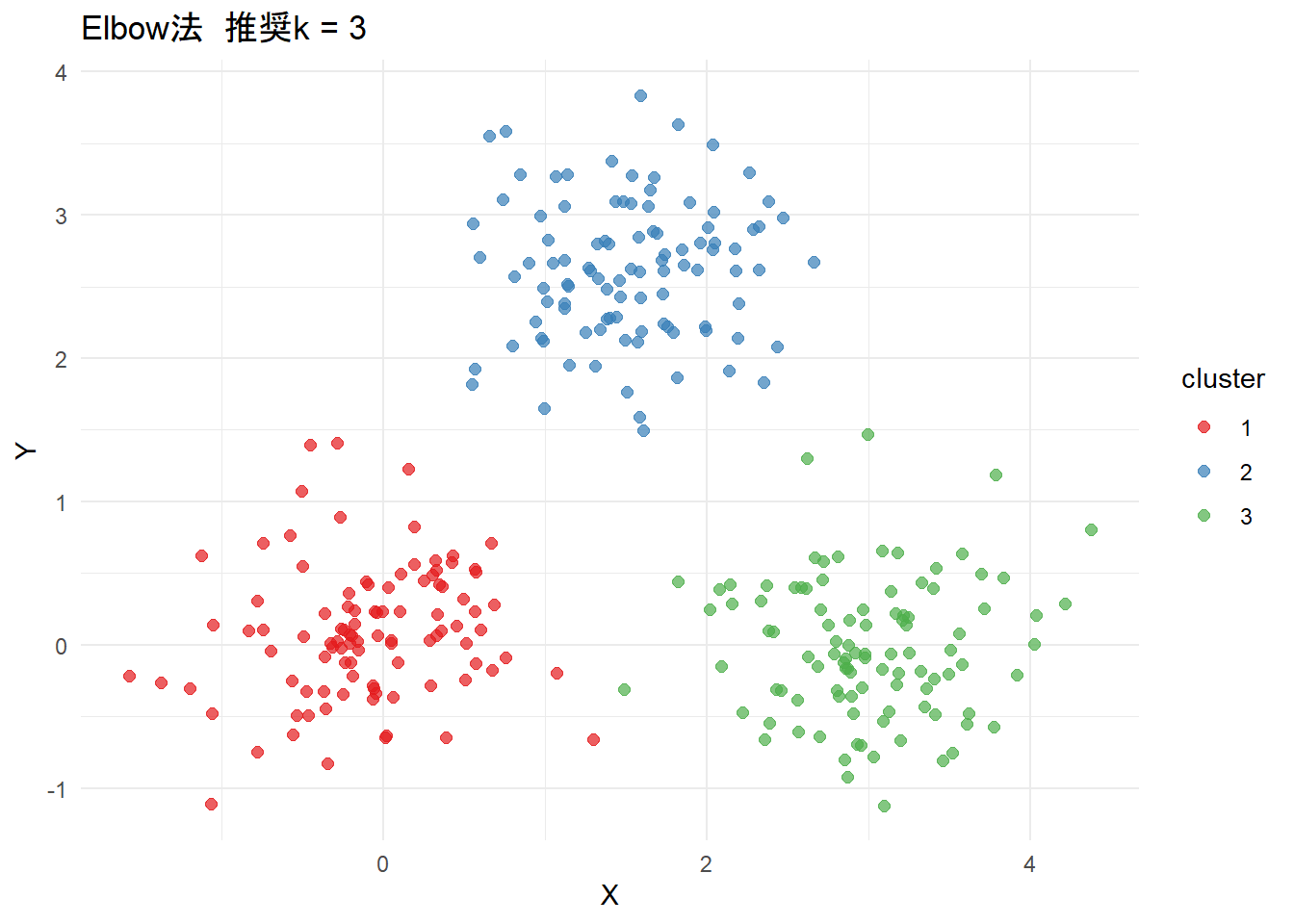
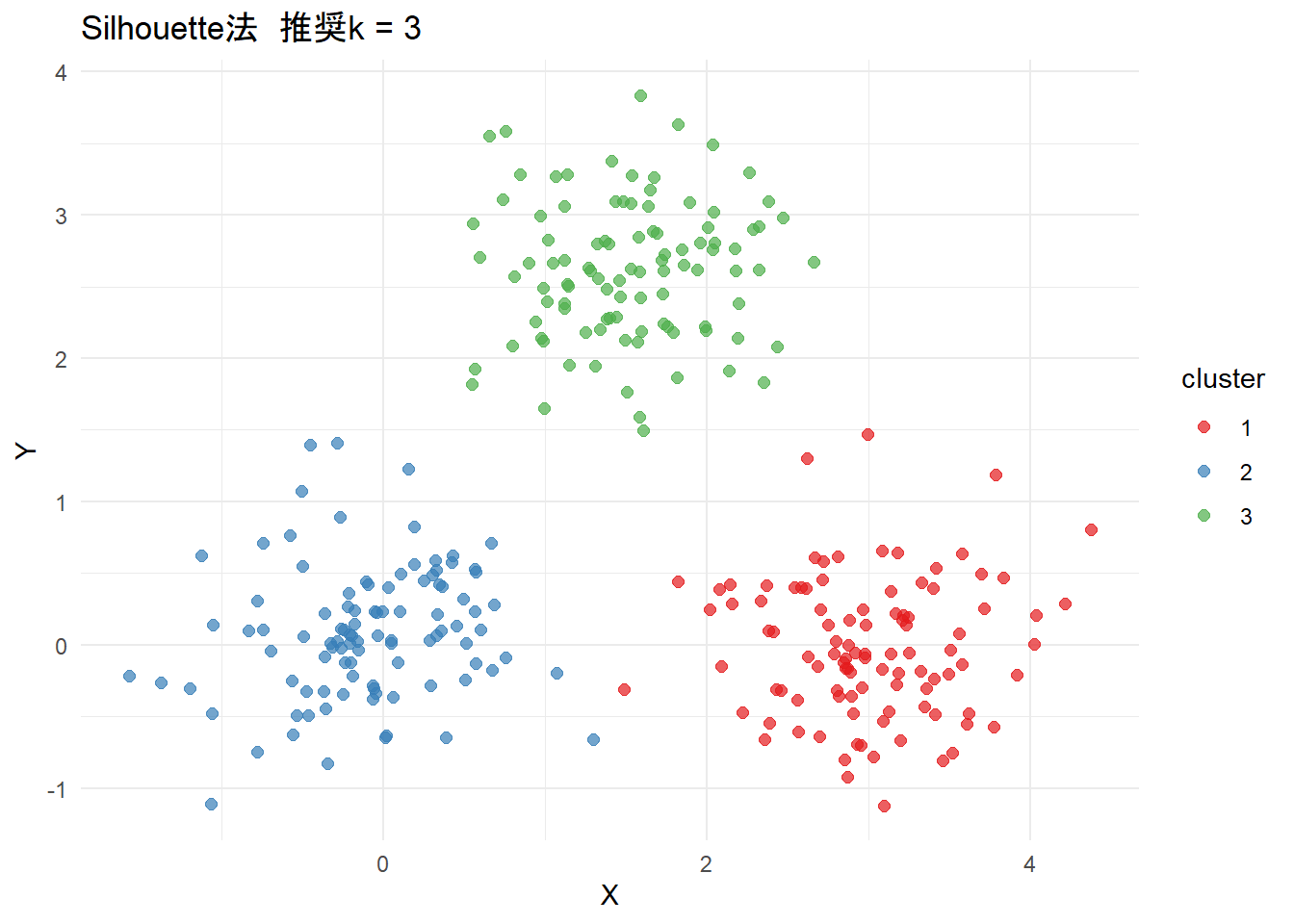
最後にクラスタリングを可視化します。
4. k-meansにおけるクラスタ数決定
1. 2次関数近似による方法 detect_elbow
SSE(クラスタ内誤差平方和)の推移を滑らかな放物線で近似し、その近似曲線から最も大きく逸脱する点(=残差が最小の点)をエルボー点とします。
k_min <- 2
k_max <- 10
k_range <- k_min:k_max
sse <- numeric(length(k_range)) # sseを格納するベクトルを初期化
for (i in seq_along(k_range)) {
km <- kmeans(data, centers = k_range[i], nstart = 20)
sse[i] <- km$tot.withinss
}- 目的: 複数の
kの値についてk-meansを実行し、それぞれのSSE(クラスタ内誤差平方和)を記録します。これは、エルボー法のグラフを描くための元データを集めるプロセスです。 -
k_range: クラスタ数kを2から10まで変化させて試します。 -
forループ:-
kmeans(...):k_rangeの各kの値でk-meansを実行します。nstart = 20は、異なる初期値で20回計算し、最も良い結果(SSEが最小の結果)を採用するためのオプションです。 -
km$tot.withinss: これがSSE(Sum of Squared Errors)、すなわち「クラスタ内誤差平方和」です。各データ点とその所属するクラスタの中心点との距離の二乗和であり、この値が小さいほどクラスタリングの性能が良いとされます。 -
sse[i] <- ...: 計算されたSSEをsseベクトルに保存します。
-
# 1. SSEのカーブを2次関数で近似する
fit <- lm(sse ~ poly(k_range, 2, raw = TRUE))
# 2. 近似した2次関数上の予測値を計算する
pred <- predict(fit, newdata = data.frame(k_range = k_range))
# 3. 実際のSSEと予測値との差(残差)を計算する
residuals <- sse - pred
# 4. 残差が最小となるkを見つける
elbow_k <- k_range[which.min(residuals)]- ステップ1:
lm(sse ~ poly(k_range, 2, raw = TRUE))-
kとsseの関係を2次多項式(放物線)で近似する線形モデル(lm)を構築します。 -
sse = a * k^2 + b * k + cという形の式で、実際のsseの点を最もよく表現する放物線を求めます。
-
- ステップ2:
predict(...)- ステップ1で作成した放物線のモデルを使って、各
kに対応するsseの予測値を計算します。これは、放物線モデルカーブ上の点の値です。
- ステップ1で作成した放物線のモデルを使って、各
- ステップ3:
residuals <- sse - pred- 残差を計算します。残差とは「観測値(
sse) - 予測値(pred)」です。 - ここでの残差は、実際のSSEの点が、放物線モデルカーブからどれだけ下に離れているかを示します。
- エルボー点では、SSEが急激に減少するため、この「放物線モデルカーブからの乖離」が最も大きくなると考えます。SSEの値は常に正ですが、この残差は負の大きな値になります。
- 残差を計算します。残差とは「観測値(
- ステップ4:
which.min(residuals)- 残差が最小(最も負に大きい値)になる点を探します。
- この点が、実際のSSEが放物線モデルカーブから最も大きく下に外れている点、つまり最も「カクンと曲がっている」点=エルボー点であると判断します。
-
which.min(residuals)はそのインデックスを返し、k_range[...]で対応するkの値を取得します。
2. シルエット係数 (Silhouette Coefficient) による方法 silhouette {cluster}
シルエット係数は、各データ点が「どれだけうまく自身のクラスタに分類されているか」を評価する指標です。具体的には、以下の2つの要素を考慮します。
- 凝集度 (Cohesion): データ点が自身のクラスタ内の他の点とどれだけ近いか。
- 分離度 (Separation): データ点が他のクラスタの点からどれだけ遠いか。
良いクラスタリングとは、クラスタ内では密に集まり(凝集度が高い)、クラスタ間では十分に離れている(分離度が高い)状態です。シルエット係数はこの度合いを-1から1の間の値で示します。
計算手順
あるデータ点 i について、シルエット係数 s(i) は以下の手順で計算されます。
ステップ1: a(i) の計算 (クラスタ内非類似度)
データ点 i が属するクラスタ内の、i 以外のすべての点との平均距離を計算します。これが凝集度を表します。
i がクラスタ \(C_k\) に属しているとします。 \[
a(i) = \frac{1}{|C_k| - 1} \sum_{j \in C_k, i \neq j} d(i, j)
\]
- \(|C_k|\): クラスタ \(C_k\) に含まれるデータ点の数
- \(d(i, j)\): データ点
iとjの間の距離(通常はユークリッド距離)
ステップ2: b(i) の計算 (クラスタ間非類似度)
データ点 i と、「i が属していない最も近いクラスタ」のすべての点との平均距離を計算します。これが分離度を表します。
i が属していない他の全てのクラスタ \(C_l (l \neq k)\) について、i との平均距離を計算し、その最小値を取ります。 \[
b(i) = \min_{l \neq k} \left\{ \frac{1}{|C_l|} \sum_{j \in C_l} d(i, j) \right\}
\]
ステップ3: s(i) の計算 (データ点 i のシルエット係数)
a(i) と b(i) を用いて、i のシルエット係数 s(i) を計算します。 \[
s(i) = \frac{b(i) - a(i)}{\max\{a(i), b(i)\}}
\]
s(i) の解釈
-
s(i)が1に近い: \(a(i) \ll b(i)\)。クラスタ内距離がクラスタ間距離よりずっと小さいことを意味し、iは非常によく分類されていると言えます。 -
s(i)が0に近い: \(a(i) \approx b(i)\)。iは2つのクラスタの境界線上にある可能性を示唆します。 -
s(i)が-1に近い: \(a(i) \gg b(i)\)。iは本来属すべきクラスタとは別のクラスタに分類されてしまっている可能性が高いです(誤分類)。
最適な k の決定方法
- いくつかの
kの候補(例:k= 2, 3, 4, …, 10)に対してk-meansを実行します。 - それぞれの
kの結果について、全データ点のシルエット係数の平均値を計算します。 - この平均値が最も高くなった
kを、最適なクラスタ数として選択します。
3. ギャップ統計量 (Gap Statistic)による clusGap {cluster}
ギャップ統計量は、クラスタリング結果の「良さ」を、データにクラスタ構造が存在しない場合(ランダムな場合)と比較するアプローチです。
基本的なアイデアは、「実際のデータのクラスタ内分散」と「ランダムに生成した参照データのクラスタ内分散」の差(ギャップ)を最大化する k を探すことです。
計算手順
ステップ1: クラスタ内分散 \(W_k\) の計算
まず、クラスタリングの性能指標として、クラスタ内の平方誤差の総和(Inertiaとも呼ばれる)を計算します。これを \(W_k\) とします。 \[
W_k = \sum_{r=1}^{k} \sum_{x_i \in C_r} \| x_i - \mu_r \|^2
\]
- \(k\): クラスタ数
- \(C_r\): \(r\)番目のクラスタ
- \(\mu_r\): クラスタ \(C_r\) の中心(セントロイド)
- \(\| \cdot \|^2\): ユークリッド距離の2乗
\(W_k\) は k が増えるほど単調に減少するため、これだけでは最適な k を決められません。
ステップ2: 参照データセットの生成と \(W_{kb}^*\) の計算
データにクラスタ構造がないという帰無仮説のもとで、参照データセットを生成します。一般的には、元のデータの各特徴量の範囲内で一様分布に従う乱数を生成します。
この参照データセットを \(B\) 個(例: B=20)生成し、それぞれに対してk-meansを実行して、クラスタ内分散 \(W_{kb}^*\) (\(b=1, 2, ..., B\)) を計算します。
ステップ3: ギャップ統計量 Gap(k) の計算
ギャップ統計量 Gap(k) は、参照データセットのクラスタ内分散の対数の期待値と、実データのクラスタ内分散の対数の差として定義されます。 \[
\text{Gap}(k) = E_n^*[\log(W_k^*)] - \log(W_k)
\]
ここで、\(E_n^*[\log(W_k^*)]\) は、B個の参照データセットから計算した \(\log(W_{kb}^*)\) の平均値で推定します。 \[
E_n^*[\log(W_k^*)] \approx \frac{1}{B} \sum_{b=1}^{B} \log(W_{kb}^*)
\]
この Gap(k) が大きいほど、ランダムなデータに比べて、実際のデータがより明確なクラスタ構造を持っていることを意味します。
ステップ4: 最適な k の決定
Gap(k) を最大化する k を探しますが、より厳密な基準が提案されています。参照データセットの \(\log(W_{kb}^*)\) の標準偏差 \(s_k\) を用います。 \[
s_k = \sqrt{\frac{1}{B} \sum_{b=1}^{B} (\log(W_{kb}^*) - E_n^*[\log(W_k^*)])^2}
\] そして、シミュレーション誤差を考慮した標準誤差 \(s'_k = s_k \sqrt{1 + 1/B}\) を計算します。
最適な k は、以下の条件を満たす最小の kとして選択されます。 \[
\text{Gap}(k) \geq \text{Gap}(k+1) - s'_{k+1}
\] これは、「k+1クラスタにしたときのギャップの改善が、統計的な誤差の範囲内であるならば、よりシンプルな k クラスタを選ぶ」という考え方に基づいています。
以上です。