Rで機械学習:サポートベクター回帰

Rで 機械学習:サポートベクター回帰 を試みます。

本ポストはこちらの続きです。

const typesetMath = (el) => { if (window.MathJax) { // MathJax Typeset window.MathJax.typeset(); } else if (window.katex...

1. サポートベクター回帰（Support Vector Regression, SVR）とは

サポートベクター回帰（SVR）は、分類問題で利用されるサポートベクターマシン（SVM）の考え方を回帰問題（数値を予測する問題）に応用したアルゴリズムです。

SVMの目的が「マージンを最大化する境界線を見つける」ことであったのに対し、SVRの目的は「できるだけ多くのデータ点が、マージンの中に収まるような回帰直線（または曲線）を見つける」ことです。

SVRの主な特徴

1. ε-チューブ（イプシロン・チューブ）

SVRの特徴的なアイデアが「ε-チューブ」です。

SVRは、まず予測を行う回帰直線（\(y = w^T x + b\)）を考えます。
次に、その直線の上下に幅 ε（イプシロン）の「チューブ」を設定します。このεは、モデルがある程度の予測誤差を許容する範囲を示し、私たちが設定するハイパーパラメータです。
SVRの目標は、このチューブの幅をできるだけ細く保ちつつ（マージン最大化に相当）、できるだけ多くのデータ点をチューブの内側に収めることです。

2. 誤差の許容とペナルティ

チューブの内側にあるデータ点は、予測誤差がε以下であると見なされ、モデルの学習において誤差はゼロとして無視されます。
チューブの外側にはみ出してしまったデータ点については、そのはみ出した距離（スラック変数 \(\xi\)）に応じてペナルティが課せられます。
SVRは、このペナルティの合計とチューブの幅のバランスを取りながら、最適な回帰モデルを学習します。

3. サポートベクター

SVMと同様に、SVRでもサポートベクターが重要な役割を果たします。SVRにおけるサポートベクターは、ε-チューブの線上、または外側にはみ出したデータ点のことです。

重要なのは、チューブの内側にあるデータ点はモデルの形状に全く影響を与えず、このサポートベクターだけが回帰直線（または曲線）の位置と形を決定するという点です。これにより、チューブ内にある多少のノイズデータに対して頑健（ロバスト）なモデルが構築できます。

4. カーネルトリック

SVMと同様、SVRでもカーネルトリックが利用できます。データが単純な直線関係にない場合でも、RBFカーネルなどを用いることで、非線形の関係を捉える滑らかな回帰曲線を見つけ出すことができます。

2. シミュレーションのシナリオ

舞台: 人気アイスクリームチェーン店のデータ分析担当者

あなたは、このアイスクリームチェーン店のデータ分析担当者です。店長から「日々の最高気温に応じて、翌日のアイスクリームの仕入れ数を調整したい」という相談を受けました。

あなたのミッションは、過去の「最高気温」と「アイスクリームの売上数」のデータを用いて、気温から売上を予測するモデルをSVRで構築することです。

分析に使用する特徴量・目的変数:

特徴量: temperature (その日の最高気温)
目的変数: sales (その日のアイスクリーム売上数)

シナリオのステップ:

基本的な売上予測（線形SVR）:
- 「気温が上がれば、売上も上がる」という、ある程度の直線的な関係を持つデータを分析します。
- 線形カーネルのSVRモデルを学習させ、「ε-チューブ」がどのように設定され、どのデータ点が「サポートベクター」になるかを可視化します。
複雑な売上予測（非線形SVR）:
- 分析を進めると、「気温が高すぎると、人々は外出を控えるため、逆に売上が落ちる」という興味深い傾向がデータから見えてきました。
- このような単純な直線では捉えきれない山なりの関係を、RBFカーネルを用いたSVRでモデル化します。
- カーネルトリックによって、SVRが非線形データにも対応できることを確認します。

3. R言語によるシミュレーションコード

準備：必要なライブラリの読み込み

# ライブラリの読み込み
library(e1071)
library(ggplot2)
library(dplyr)

ステップ1：基本的な売上予測（線形SVR）

# 再現性のための乱数シード設定
seed <- 20250816
set.seed(seed)


# データ生成
# 気温とアイスクリーム売上のデータ（線形関係）を生成します。
n <- 100
temperature <- runif(n, 15, 35)
sales <- 10 * temperature - 50 + rnorm(n, mean = 0, sd = 30)
icecream_data_linear <- data.frame(temperature, sales)

epsilon_value <- 40

svr_linear_model <- svm(sales ~ temperature,
  data = icecream_data_linear,
  type = "eps-regression",
  kernel = "linear",
  epsilon = epsilon_value / sd(sales),
  cost = 10
)

# 予測値とサポートベクターを取得
icecream_data_linear$predicted_sales <- predict(svr_linear_model, icecream_data_linear)
support_vectors_linear <- icecream_data_linear[svr_linear_model$index, ]

# 可視化
p_svr_linear <- ggplot(icecream_data_linear, aes(x = temperature, y = sales)) +
  geom_point(aes(color = "データ点"), alpha = 0.7) + # 元のデータ
  geom_line(aes(y = predicted_sales, color = "SVR予測"), linewidth = 1.2) + # SVRによる予測直線
  geom_ribbon(
    aes(
      y = predicted_sales,
      ymin = predicted_sales - epsilon_value,
      ymax = predicted_sales + epsilon_value,
      fill = "ε-チューブ"
    ),
    alpha = 0.2
  ) +

  # サポートベクターを強調表示
  geom_point(
    data = support_vectors_linear, aes(x = temperature, y = sales, shape = "サポートベクター"),
    fill = "blue", color = "blue", size = 4
  ) +

  # 凡例と色の設定
  scale_color_manual(name = "", values = c("データ点" = "gray50", "SVR予測" = "red")) +
  scale_fill_manual(name = "", values = c("ε-チューブ" = "red")) +
  scale_shape_manual(name = "", values = c("サポートベクター" = 1)) +
  labs(
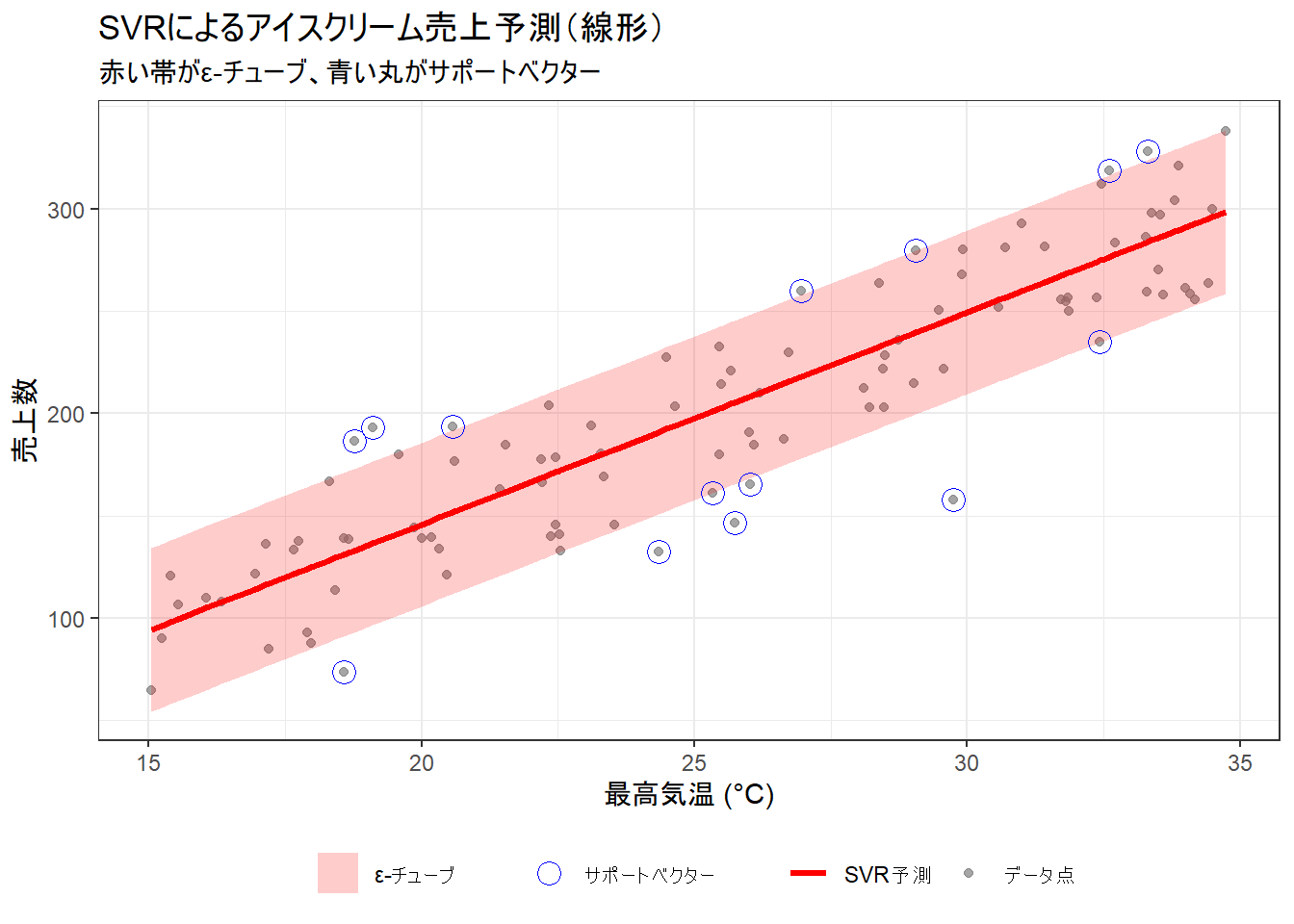
    title = "SVRによるアイスクリーム売上予測（線形）",
    subtitle = "赤い帯がε-チューブ、青い丸がサポートベクター",
    x = "最高気温 (°C)",
    y = "売上数"
  ) +
  theme_bw() +
  theme(legend.position = "bottom")

print(p_svr_linear)

Figure 1 の解説

赤い実線が、SVRによって学習された予測モデルです。
薄い赤い帯が「ε-チューブ」です。このチューブの内側にあるデータ点は、モデルの学習において予測誤差が無視されています。
青い丸で囲まれた「サポートベクター」は、チューブの境界線上または外側にある点です。
サポートベクターだけが赤い線の位置と傾きを決定しています。

ステップ2：非線形な売上予測（非線形SVR）

# 再現性のための乱数シード設定
set.seed(seed)


# データ生成
# 「気温が高すぎると売上が落ちる」という非線形な関係を持つデータを生成します。
n <- 150
temperature_nl <- runif(n, 10, 45)
sales_nl <- -0.8 * (temperature_nl - 32)^2 + 300 + rnorm(n, mean = 0, sd = 40)
icecream_data_nonlinear <- data.frame(temperature = temperature_nl, sales = sales_nl)

epsilon_value_nl <- 50

svr_rbf_model <- svm(sales ~ temperature,
  data = icecream_data_nonlinear,
  type = "eps-regression",
  kernel = "radial",
  epsilon = epsilon_value_nl / sd(sales_nl),
  cost = 10,
  gamma = 0.1
)

# 予測値とサポートベクターを取得
plot_grid <- data.frame(temperature = seq(min(temperature_nl), max(temperature_nl), length.out = 200))
plot_grid$predicted_sales <- predict(svr_rbf_model, plot_grid)
support_vectors_rbf <- icecream_data_nonlinear[svr_rbf_model$index, ]


# 可視化
p_svr_rbf <- ggplot(icecream_data_nonlinear, aes(x = temperature, y = sales)) +
  geom_point(aes(color = "データ点"), alpha = 0.7) +
  geom_line(data = plot_grid, aes(y = predicted_sales, color = "SVR予測"), linewidth = 1.2) +
  geom_ribbon(
    data = plot_grid,
    aes(
      y = predicted_sales,
      ymin = predicted_sales - epsilon_value_nl,
      ymax = predicted_sales + epsilon_value_nl,
      fill = "ε-チューブ"
    ),
    alpha = 0.2
  ) +
  geom_point(
    data = support_vectors_rbf, aes(x = temperature, y = sales, shape = "サポートベクター"),
    fill = "blue", color = "blue", size = 4
  ) +

  # 凡例と色の設定
  scale_color_manual(name = "", values = c("データ点" = "gray50", "SVR予測" = "red")) +
  scale_fill_manual(name = "", values = c("ε-チューブ" = "red")) +
  scale_shape_manual(name = "", values = c("サポートベクター" = 1)) +
  labs(
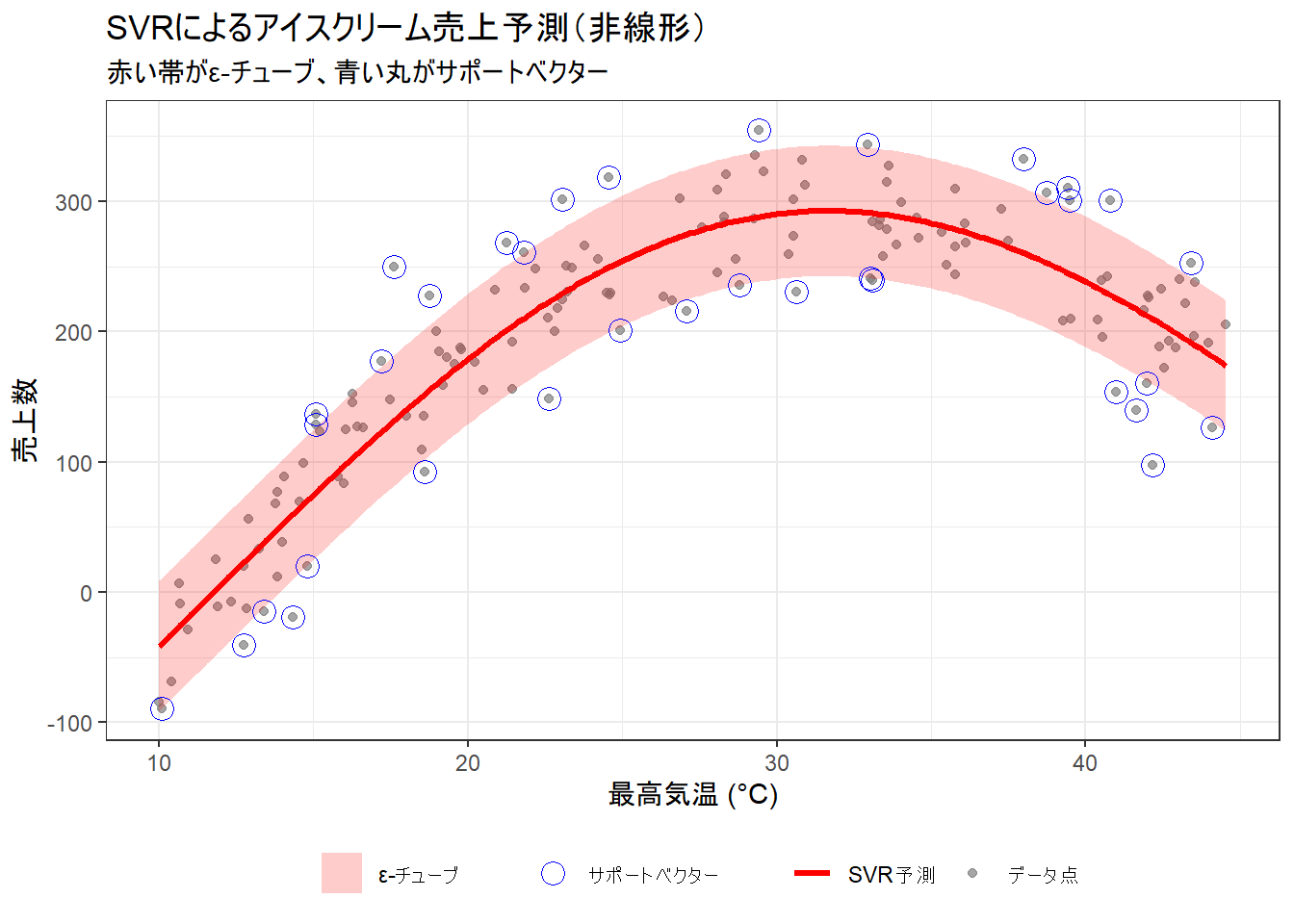
    title = "SVRによるアイスクリーム売上予測（非線形）",
    subtitle = "赤い帯がε-チューブ、青い丸がサポートベクター",
    x = "最高気温 (°C)",
    y = "売上数"
  ) +
  theme_bw() +
  theme(legend.position = "bottom")

print(p_svr_rbf)