Rで 統計的因果推論:自然実験-差分の差分法 を試みます。
本ポストはこちらの続きです。

1. 「自然実験」とは
統計的因果推論において、ある介入(処置)が結果(アウトカム)に与える因果効果を測るための信頼性の高い方法の一つはランダム化比較試験(RCT)です。RCTでは、研究対象者をランダムに介入群と対照群に分け、その後の結果を比較することで、介入以外の要因が結果に与える影響(セレクションバイアスなど)を排除し、純粋な因果効果を推定します。
しかし、社会科学、経済学、公衆衛生学などの分野では、倫理的・現実的な制約からRCTを実施できないケースが数多くあります。例えば、「最低賃金を引き上げることが雇用に与える影響」を調べるために、ランダムに選んだ都市の最低賃金だけを引き上げる、といった実験は現実的ではありません。
そこで登場するのが「自然実験(Natural Experiment)」というアプローチです。
自然実験とは、研究者が介入を人為的に割り当てるのではなく、あたかもランダムに割り振られたかのような状況が、法律の改正、政策の変更、自然災害といった外的要因によって「自然に」発生した場合に、その状況を利用して因果効果を推定する手法です。
自然実験は、RCTが実施不可能な状況において、セレクションバイアスを軽減し、より信頼性の高い因果関係を探るための有用なツールとなります。代表的な分析手法として、差分の差分法(Difference-in-Differences, DID)、回帰不連続デザイン(Regression Discontinuity Design, RDD)、操作変数法(Instrumental Variable, IV)などがあります。
今回は、差分の差分法(DID)を用いたシミュレーションを行います。
2. シミュレーションのシナリオ:「新設図書館は子供たちの読書時間を増やすか?」
ある研究者が、地域の公共投資が子供たちの教育に与える影響に関心を持っているとします。
【状況設定】
- 隣接する「A市」と「B市」があります。両市は社会経済的な特徴が似ています。
- 2022年の初めに、A市は市の重点プロジェクトとして新しい近代的な図書館を建設し、オープンしました。
- 一方、B市は財政的な理由で図書館の建設計画を見送りました。
- この図書館建設の決定は、研究者の意図とは無関係に行われました。これは、研究者が介入をコントロールできない「自然実験」の状況とみなせます。
【研究の問い】
- A市の新しい図書館の建設は、A市の子供たちの読書時間に因果的な影響を与えたのでしょうか?
【分析デザイン:差分の差分法(DID)】
- 介入群(Treatment Group): 新しい図書館が建設されたA市の子供たち
- 対照群(Control Group): 図書館が建設されなかったB市の子供たち
- 介入前の期間: 2021年
- 介入後の期間: 2023年
単純に介入後のA市とB市の読書時間を比較するだけでは、元々A市の方が教育熱心な家庭が多く、読書時間が長いかもしれません(セレクションバイアス)。また、単純にA市の介入前後の読書時間を比較するだけでは、スマートフォンや他の娯楽の普及といった、図書館とは無関係な時代全体のトレンドの影響を受けている可能性があります。
そこで、以下の設計に基づき、差分の差分法(DID)を利用します。
- 差分1(時間変化):
- A市(介入群)における介入前後の読書時間の「変化量」を計算する。
- B市(対照群)における介入前後の読書時間の「変化量」を計算する。B市の変化量は、図書館がなくても生じたであろう「自然なトレンド」を捉えていると考える。
- 差分2(差分の差):
- A市の変化量からB市の変化量を差し引く。
- この「差の差」が、自然なトレンドの影響を取り除いた、図書館建設による純粋な因果効果(Average Treatment Effect on the Treated, ATT)の推定値となります。
この計算の背景には、「平行トレンドの仮定(Parallel Trend Assumption)」という重要な仮定があります。これは、「もしA市に図書館が建設されなかったとしても、A市の読書時間のトレンドはB市のトレンドと平行に推移したであろう」という仮定です。この仮定が満たされていれば、DIDは妥当な因果効果を推定できます。逆に、平行トレンドの仮定が満たされていなければ、分析結果は全く信用できません。
因果効果\(\hat{\delta}_{DID}\)は以下のように計算されます。\(Y\)は結果(読書時間)、\(T\)は介入群、\(C\)は対照群、\(Post\)は介入後、\(Pre\)は介入前を示します。
\[
\hat{\delta}_{DID} = \left( E\left[Y | T, Post\right] - E\left[Y | T, Pre\right] \right) - \left( E\left[Y | C, Post\right] - E\left[Y | C, Pre\right] \right)
\]
それでは、このシナリオをRでシミュレーションしてみましょう。
3. Rによるシミュレーション
3.1. シミュレーションの準備とデータ生成
まず、必要なパッケージを読み込み、シナリオに沿ったシミュレーションデータを作成します。
- A市とB市、それぞれ500人の子供たちのデータを生成します。
- A市はもともとB市より平均読書時間が少し長い(週に0.5時間)と設定します。
- 時間経過による自然なトレンドとして、両市ともに読書時間が少し減少する(週に0.2時間)と設定します。
- 図書館建設の真の因果効果として、A市の子供たちの読書時間は、このトレンドに加えて週に1.5時間増加すると設定します。
- 個人のばらつきを表す誤差も加えます。
# 必要なパッケージを読み込み
library(tidyverse)
library(knitr)
# 結果を再現可能にするための乱数シード設定
seed <- 20250825
set.seed(seed)
# シミュレーションのパラメータ設定
n <- 500 # 各市のサンプルサイズ
city_a_effect <- 0.5 # A市が元々持つ読書時間の優位性(時間)
time_trend <- -0.2 # 時間経過による自然な変化(時間)
treatment_effect <- 1.5 # 図書館建設の真の因果効果(時間)
# データ生成
sim_data <- tibble(
# 子供のID
child_id = 1:(n * 2 * 2),
# 市(A市が介入群、B市が対照群)
city = rep(c("A市(介入群)", "B市(対照群)"), each = n * 2),
# 時期(介入前:2021年、介入後:2023年)
time = rep(rep(c("介入前 (2021年)", "介入後 (2023年)"), each = n), 2)
) |>
# 介入ダミー変数と時期ダミー変数を追加
mutate(
# 介入群(A市)なら1、対照群(B市)なら0
treated = if_else(city == "A市(介入群)", 1, 0),
# 介入後なら1、介入前なら0
post = if_else(time == "介入後 (2023年)", 1, 0)
) |>
# 結果変数(週平均読書時間)を生成
mutate(
reading_time = 5 + # 全体のベースライン読書時間
city_a_effect * treated + # A市の元々の特性
time_trend * post + # 時間経過によるトレンド
treatment_effect * treated * post + # 介入(treated=1)かつ介入後(post=1)の因果効果
rnorm(n * 2 * 2, mean = 0, sd = 1.5), # 個人のばらつき
.keep = "all"
) |>
# 時期を因子型に変換(プロットの順序のため)
mutate(time = factor(time, levels = c("介入前 (2021年)", "介入後 (2023年)")))
# 生成したデータの最初の数行を表示
cat("##### 生成されたデータの一部 #####\n")
kable(head(sim_data))##### 生成されたデータの一部 #####| child_id | city | time | treated | post | reading_time |
|---|---|---|---|---|---|
| 1 | A市(介入群) | 介入前 (2021年) | 1 | 0 | 7.616123 |
| 2 | A市(介入群) | 介入前 (2021年) | 1 | 0 | 7.758057 |
| 3 | A市(介入群) | 介入前 (2021年) | 1 | 0 | 5.297896 |
| 4 | A市(介入群) | 介入前 (2021年) | 1 | 0 | 4.175875 |
| 5 | A市(介入群) | 介入前 (2021年) | 1 | 0 | 5.726155 |
| 6 | A市(介入群) | 介入前 (2021年) | 1 | 0 | 7.442247 |
reading_timeが結果変数です。
また、コード中のtreatment_effect * treated * postの項が、A市が介入後(2023年)にのみ受ける図書館建設の効果を表しています。
3.2. 差分の差分法(DID)による効果の推定
次に、生成したデータを使ってDID分析を行います。グループごとの平均値を計算し、「差の差」を求めて因果効果を推定します。
# グループごとの平均読書時間を計算
summary_stats <- sim_data |>
group_by(city, time) |>
summarise(
mean_reading_time = mean(reading_time),
.groups = "drop"
)
cat("##### グループごとの平均読書時間 #####\n")
kable(summary_stats, digits = 2)
# DID推定値の計算
# 1. 各市の介入前後の平均値を取得
y_a_pre <- summary_stats$mean_reading_time[summary_stats$city == "A市(介入群)" & summary_stats$time == "介入前 (2021年)"]
y_a_post <- summary_stats$mean_reading_time[summary_stats$city == "A市(介入群)" & summary_stats$time == "介入後 (2023年)"]
y_b_pre <- summary_stats$mean_reading_time[summary_stats$city == "B市(対照群)" & summary_stats$time == "介入前 (2021年)"]
y_b_post <- summary_stats$mean_reading_time[summary_stats$city == "B市(対照群)" & summary_stats$time == "介入後 (2023年)"]
# 2. 差分1(時間変化)の計算
diff_a <- y_a_post - y_a_pre
diff_b <- y_b_post - y_b_pre
cat("\n##### 差分1:各市の時間変化 #####\n")
cat("A市(介入群)の変化量:", round(diff_a, 3), "時間\n")
cat("B市(対照群)の変化量:", round(diff_b, 3), "時間\n")
# 3. 差分2(差分の差)の計算
did_estimate <- diff_a - diff_b
cat("\n##### 差分2:差分の差(DID推定値) #####\n")
cat(
"DID推定値 (A市の変化量 - B市の変化量):",
round(did_estimate, 3),
"時間\n"
)
cat(
"この値が、図書館建設による読書時間への因果効果の推定値です。\n"
)##### グループごとの平均読書時間 #####| city | time | mean_reading_time |
|---|---|---|
| A市(介入群) | 介入前 (2021年) | 5.45 |
| A市(介入群) | 介入後 (2023年) | 6.69 |
| B市(対照群) | 介入前 (2021年) | 4.89 |
| B市(対照群) | 介入後 (2023年) | 4.76 |
##### 差分1:各市の時間変化 #####
A市(介入群)の変化量: 1.242 時間
B市(対照群)の変化量: -0.135 時間
##### 差分2:差分の差(DID推定値) #####
DID推定値 (A市の変化量 - B市の変化量): 1.377 時間
この値が、図書館建設による読書時間への因果効果の推定値です。計算の結果、DID推定値は1.377時間となりました。これは、私たちがデータ生成時に設定した真の因果効果(1.5時間)に近い値です。この結果から、DID分析によって、元々の都市間の差や全体の時間トレンドの影響を除去し、図書館建設の純粋な効果を推定できたことがわかります。
3.3. 結果の可視化
最後に、この結果をggplotで可視化します。
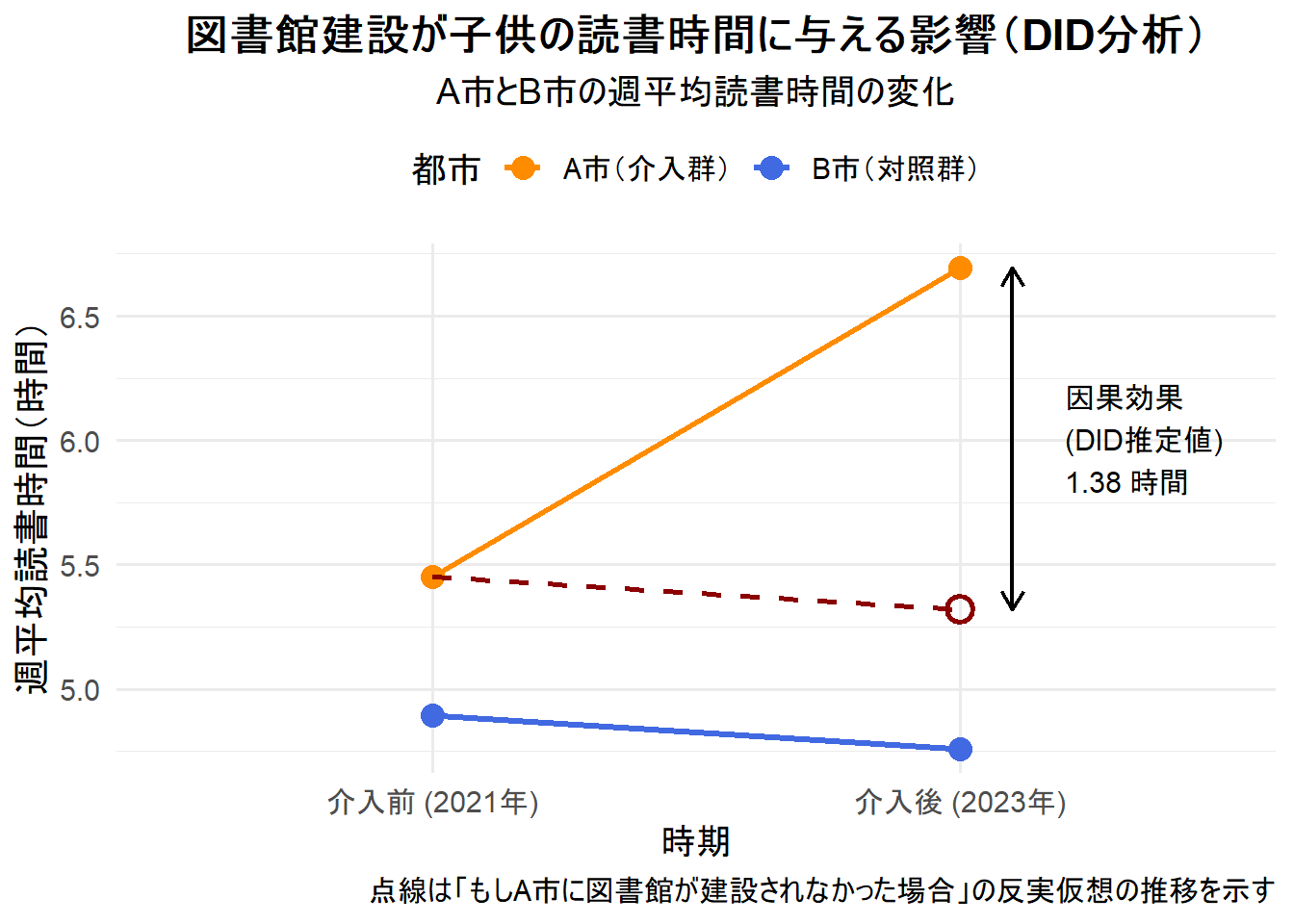
- A市とB市の平均読書時間の推移を線で結びます。
- 「もしA市に図書館が建設されなかったらどうなっていたか」という反実仮想(Counterfactual)の線を描画します。これは、B市のトレンド(線の傾き)をA市の介入前の点から平行に伸ばしたものです。
- 実際のA市の介入後の点と、この反実仮想の点との差が、DIDによって推定された因果効果となります。
# 反実仮想のデータポイントを計算
# (A市の介入前の値 + B市のトレンド)
counterfactual_a_post <- y_a_pre + diff_b
# プロットの作成
did_plot <- ggplot(
summary_stats,
aes(x = time, y = mean_reading_time, group = city, color = city)
) +
geom_line(aes(linetype = city), linewidth = 1.2) +
geom_point(size = 4) +
# 反実仮想の線を描画 (A市の介入前 -> 反実仮想の介入後)
geom_segment(
aes(
x = "介入前 (2021年)", xend = "介入後 (2023年)",
y = y_a_pre, yend = counterfactual_a_post
),
color = "darkred",
linetype = "dashed",
linewidth = 1
) +
# 反実仮想の点を描画
geom_point(
aes(x = "介入後 (2023年)", y = counterfactual_a_post),
color = "darkred",
shape = 1,
size = 4,
stroke = 1.5
) +
# 因果効果を示す矢印とテキスト
geom_segment(
aes(
x = 2.1, xend = 2.1,
y = counterfactual_a_post, yend = y_a_post
),
arrow = arrow(length = unit(0.3, "cm"), ends = "both"),
color = "black",
linewidth = 0.8
) +
annotate(
"text",
x = 2.2,
y = (y_a_post + counterfactual_a_post) / 2,
label = paste0("因果効果\n(DID推定値)\n", round(did_estimate, 2), " 時間"),
hjust = 0,
vjust = 0.5,
size = 4
) +
# スケールとラベルの設定
scale_color_manual(
values = c("A市(介入群)" = "darkorange", "B市(対照群)" = "royalblue"),
name = "都市"
) +
scale_linetype_manual(
values = c("A市(介入群)" = "solid", "B市(対照群)" = "solid"),
guide = "none"
) +
labs(
title = "図書館建設が子供の読書時間に与える影響(DID分析)",
subtitle = "A市とB市の週平均読書時間の変化",
x = "時期",
y = "週平均読書時間(時間)",
caption = "点線は「もしA市に図書館が建設されなかった場合」の反実仮想の推移を示す"
) +
theme_minimal(base_size = 14) +
theme(
legend.position = "top",
plot.title = element_text(hjust = 0.5, face = "bold"),
plot.subtitle = element_text(hjust = 0.5)
)
# プロットを表示
print(did_plot)以上です。