Rで 統計的因果推論:自然実験-操作変数法 を試みます。
本ポストはこちらの続きです。

Rの関数 ivreg {AER} については、こちらを参照してください。

1. 「操作変数法(IV)」とは
操作変数法(Instrumental Variable, IV method)は、統計的因果推論において、観測できない交絡因子によって引き起こされる内生性(endogeneity)の問題に対処し、因果効果を推定するための手法です。
なぜ操作変数法が必要か?:内生性の問題
ある介入(例:大学教育)が結果(例:年収)に与える影響を、単純な回気分析(OLS)で調べようとすると、しばしばバイアス(偏り)が生じます。その主な原因が「省略された変数バイアス」です。
例えば、「個人の能力や意欲」といった観測できない交絡因子があったとします。能力が高い人は、次の2つの特徴を持つ傾向があります。
- 大学に進学しやすい(介入を受けやすい)。
- 教育の影響とは別に、元々高い収入を得るポテンシャルがある。
この場合、「能力」という共通の原因が「大学進学」という介入と「年収」という結果の両方に影響を与えてしまいます。そのため、単純に大卒者と非大卒者の年収を比較しても、その差が純粋な教育の効果なのか、元々の能力の差なのかを区別できません。
このように、分析モデルに含まれていない要因(この場合は能力)が介入変数(大学進学)と誤差項(年収に影響を与える能力などの観測外要因)の両方と相関してしまう状態を内生性と呼びます。操作変数法は、この内生性の問題を解決するために用いられます。
操作変数(IV)の役割
操作変数法は、この内生性の問題を解決するために、操作変数(Instrumental Variable, IV)と呼ばれる第3の変数Zを利用します。操作変数Zは、以下の3つの条件を満たす必要があります。
- 関連性 (Relevance): 操作変数
Zは、内生的な介入変数X(例:大学進学)と相関している必要があります。 (\(\text{Cov}\left(Z, X\right) \neq 0\)) - 除外制約 (Exclusion Restriction): 操作変数
Zは、結果Y(例:年収)に対して、Xを経由する以外に直接的な影響を与えません。また、Zは結果Yに影響を与える観測できない要因(例:能力)とも相関しません。 (\(\text{Cov}\left(Z, u\right) = 0\), ここで\(u\)は誤差項) - 単調性 (Monotonicity): 操作変数
Zが変化したとき、全ての人が同じ方向に影響を受ける(介入を受けやすくなる or なりにくくなる)と仮定します。
これらの条件を満たす操作変数を見つけることで、介入変数Xのうち、操作変数Zによって外生的に動かされた部分だけを取り出し、その部分が結果Yに与える影響を推定することができます。これにより、交絡因子の影響を分離し、より真の因果効果に近い値を推定することが可能になります。代表的な推定方法に2段階最小二乗法(2SLS)があります。
2. シミュレーションのシナリオ:「大学進学は年収を上げるか?」
【研究の問い】
- 大学に進学すること(介入)は、将来の年収(結果)に対してどの程度の因果効果を持つのでしょうか?
【問題設定】
- 介入変数 (X): 大学進学の有無(大卒なら1, そうでなければ0)
- 結果変数 (Y): 30歳時点の年収
- 観測できない交絡因子 (U): 個人の潜在的な「能力・意欲」。これはデータ上では観測できません。能力が高い人は大学に進学しやすく、かつ年収も高くなる傾向があります。
- 操作変数 (Z): 「高校の近くに大学のキャンパスが新設されたか」というダミー変数(新設された地域なら1, されなければ0)。
【操作変数の妥当性】
- 関連性: 自宅近くに大学ができれば、物理的・心理的な進学コストが下がり、これまで進学を諦めていた層が進学しやすくなる可能性があります。したがって、キャンパス新設(
Z)は大学進学(X)と相関すると考えられます。 - 除外制約: キャンパスが新設されたかどうかという事実は、個人の潜在的な能力(
U)とは無関係です。また、キャンパス新設自体が、大学進学という経路を通らずに直接その人の年収(Y)を上げるとは考えにくいです(※)。この仮定がIV分析の根幹です。
(※)厳密には、キャンパス新設が地域の経済を活性化させ、親の収入などを通じて間接的に影響する可能性も考えられますが、シミュレーションではこの除外制約が満たされている理想的な状況を仮定します。
3. Rによるシミュレーション
3.1. シミュレーションの準備とデータ生成
まず、必要なパッケージを読み込み、シナリオに沿ったシミュレーションデータを作成します。
- 5000人の仮想的な個人データを生成します。
- 観測できない交絡因子「能力
U」を生成します。 - 操作変数「キャンパス新設
Z」をランダムに割り振ります。 - 大学進学
Xは、「能力U」と「キャンパス新設Z」の両方に影響されるように設定します。 - 年収
Yは、「大学進学X」と「能力U」の両方に影響されるように設定します。 - 大学進学の真の因果効果は、年収を150万円増加させると設定します。
# 必要なパッケージを読み込み
library(tidyverse)
library(AER) # 操作変数法のためのivreg関数を含む
library(knitr)
# 結果を再現可能にするための乱数シード設定
seed <- 20250829
set.seed(seed)
# シミュレーションのパラメータ設定
n <- 5000 # サンプルサイズ
beta_x <- 150 # ★大学進学(X)が年収(Y)に与える真の因果効果 (150万円)★
gamma_u <- 50 # 能力(U)が年収(Y)に与える効果 (交絡の強さ)
alpha_u <- 1.5 # 能力(U)が大学進学(X)に与える効果
alpha_z <- 0.8 # キャンパス新設(Z)が大学進学(X)に与える効果 (操作変数の強さ)
# データ生成
# 1. 外生変数 (U, Z) の生成
# U: 観測できない能力 (交絡因子)
# Z: キャンパス新設の有無 (操作変数)
sim_data_iv <- tibble(
id = 1:n,
ability_u = rnorm(n, mean = 0, sd = 1),
campus_z = rbinom(n, size = 1, prob = 0.5) # 50%の地域で新設
)
# 2. 内生変数 (X) の生成
# 大学進学の有無は、能力(U)とキャンパス新設(Z)に依存
prob_x <- plogis(-1 + alpha_u * sim_data_iv$ability_u + alpha_z * sim_data_iv$campus_z)
sim_data_iv <- sim_data_iv |>
mutate(
college_x = rbinom(n, size = 1, prob = prob_x)
)
# 3. 結果変数 (Y) の生成
# 年収は、大学進学(X)と能力(U)に依存
sim_data_iv <- sim_data_iv |>
mutate(
income_y = 300 + beta_x * college_x + gamma_u * ability_u + rnorm(n, mean = 0, sd = 50),
# 読みやすさのため変数名を日本語に
年収_Y = income_y,
大学進学_X = factor(college_x, labels = c("非大卒", "大卒")),
キャンパス新設_Z = factor(campus_z, labels = c("なし", "あり")),
能力_U = ability_u
) |>
select(年収_Y, 大学進学_X, キャンパス新設_Z, 能力_U)
# 生成したデータのプレビュー
cat("##### 生成されたデータの一部 #####\n")
kable(head(sim_data_iv))##### 生成されたデータの一部 #####| 年収_Y | 大学進学_X | キャンパス新設_Z | 能力_U |
|---|---|---|---|
| 368.2234 | 大卒 | なし | 0.2968237 |
| 484.6730 | 大卒 | なし | 0.4807284 |
| 395.9822 | 大卒 | なし | -0.5505610 |
| 138.0127 | 非大卒 | なし | -1.7780336 |
| 376.1266 | 大卒 | あり | -1.2761547 |
| 182.6901 | 非大卒 | なし | -1.5868684 |
能力_Uが大学進学_Xと年収_Yの両方に影響を与えているために内生性が生じているサンプルデータです。
3.2. バイアスのあるOLS推定 vs 操作変数法(2SLS)による推定
まず、内生性を無視して単純な回帰分析(OLS)を行い、次に操作変数法(2SLS)で分析して結果を比較します。AERパッケージのivreg()関数を使います。
# 数値として扱うためにダミー変数を再作成
sim_data_iv <- sim_data_iv |>
mutate(
college_x_num = as.numeric(大学進学_X) - 1,
campus_z_num = as.numeric(キャンパス新設_Z) - 1
)
# 1. 単純なOLS回帰(バイアスあり)
# 年収 ~ 大学進学
model_ols <- lm(年収_Y ~ college_x_num, data = sim_data_iv)
cat("##### (1) OLSによる推定結果(バイアスあり) #####\n")
summary(model_ols)
# 2. 操作変数法(2SLS)による推定
# ivreg(結果 ~ 内生変数 | 操作変数)
model_iv <- ivreg(年収_Y ~ college_x_num | campus_z_num, data = sim_data_iv)
cat("\n##### (2) 操作変数法(2SLS)による推定結果 #####\n")
summary(model_iv)##### (1) OLSによる推定結果(バイアスあり) #####
Call:
lm(formula = 年収_Y ~ college_x_num, data = sim_data_iv)
Residuals:
Min 1Q Median 3Q Max
-230.899 -44.803 0.546 45.007 238.846
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 280.003 1.210 231.4 <2e-16 ***
college_x_num 201.116 1.919 104.8 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 66.4 on 4998 degrees of freedom
Multiple R-squared: 0.6874, Adjusted R-squared: 0.6873
F-statistic: 1.099e+04 on 1 and 4998 DF, p-value: < 2.2e-16
##### (2) 操作変数法(2SLS)による推定結果 #####
Call:
ivreg(formula = 年収_Y ~ college_x_num | campus_z_num, data = sim_data_iv)
Residuals:
Min 1Q Median 3Q Max
-233.7139 -47.8866 -0.6048 47.9246 243.6634
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 299.262 6.588 45.428 <2e-16 ***
college_x_num 152.702 16.369 9.329 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 70.5 on 4998 degrees of freedom
Multiple R-Squared: 0.6475, Adjusted R-squared: 0.6475
Wald test: 87.02 on 1 and 4998 DF, p-value: < 2.2e-16 【結果の読み方】
- OLSの結果:
college_x_numの係数(Estimate)は201.116です。これは、私たちが設定した真の因果効果150よりも大きい値です。これは、元々の能力が高い人が大学に進学する傾向があるため、教育の効果が過大評価されていることを示しています。これが内生性によるバイアスです。 - 操作変数法(2SLS)の結果:
college_x_numの係数は152.702です。この値は、真の因果効果150に近い結果です。操作変数「キャンパス新設」を用いることで、能力による交絡の影響を取り除き、大学進学の純粋な因果効果を推定できたことがわかります。
3.3. 操作変数の「関連性」のチェック(第1ステージ)
操作変数法がうまく機能するためには、操作変数Zが内生変数Xと相関している必要があります。これは、2SLSの第1ステージの回帰で確認できます。
# 第1ステージの回帰:大学進学 ~ キャンパス新設
model_first_stage <- lm(college_x_num ~ campus_z_num, data = sim_data_iv)
cat("##### 第1ステージの回帰結果(操作変数の関連性チェック) #####\n")
summary(model_first_stage)##### 第1ステージの回帰結果(操作変数の関連性チェック) #####
Call:
lm(formula = college_x_num ~ campus_z_num, data = sim_data_iv)
Residuals:
Min 1Q Median 3Q Max
-0.4590 -0.4590 -0.3372 0.5410 0.6628
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.337182 0.009691 34.792 <2e-16 ***
campus_z_num 0.121822 0.013739 8.867 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4857 on 4998 degrees of freedom
Multiple R-squared: 0.01549, Adjusted R-squared: 0.01529
F-statistic: 78.62 on 1 and 4998 DF, p-value: < 2.2e-16【結果の読み方】
-
campus_z_numの係数は0.121822で、p値(Pr(>|t|))は<2e-16です。これは、「キャンパスが新設されると、大学進学率が有意(5%)に約12.2%ポイント上昇する」ことを意味しています。 - 一番下のF-statisticが
78.62と示されています(帰無仮説は全ての係数が0)。経験則として、このF値が10以上であれば、操作変数は十分に強く、「弱操作変数」の問題はないと判断されます。
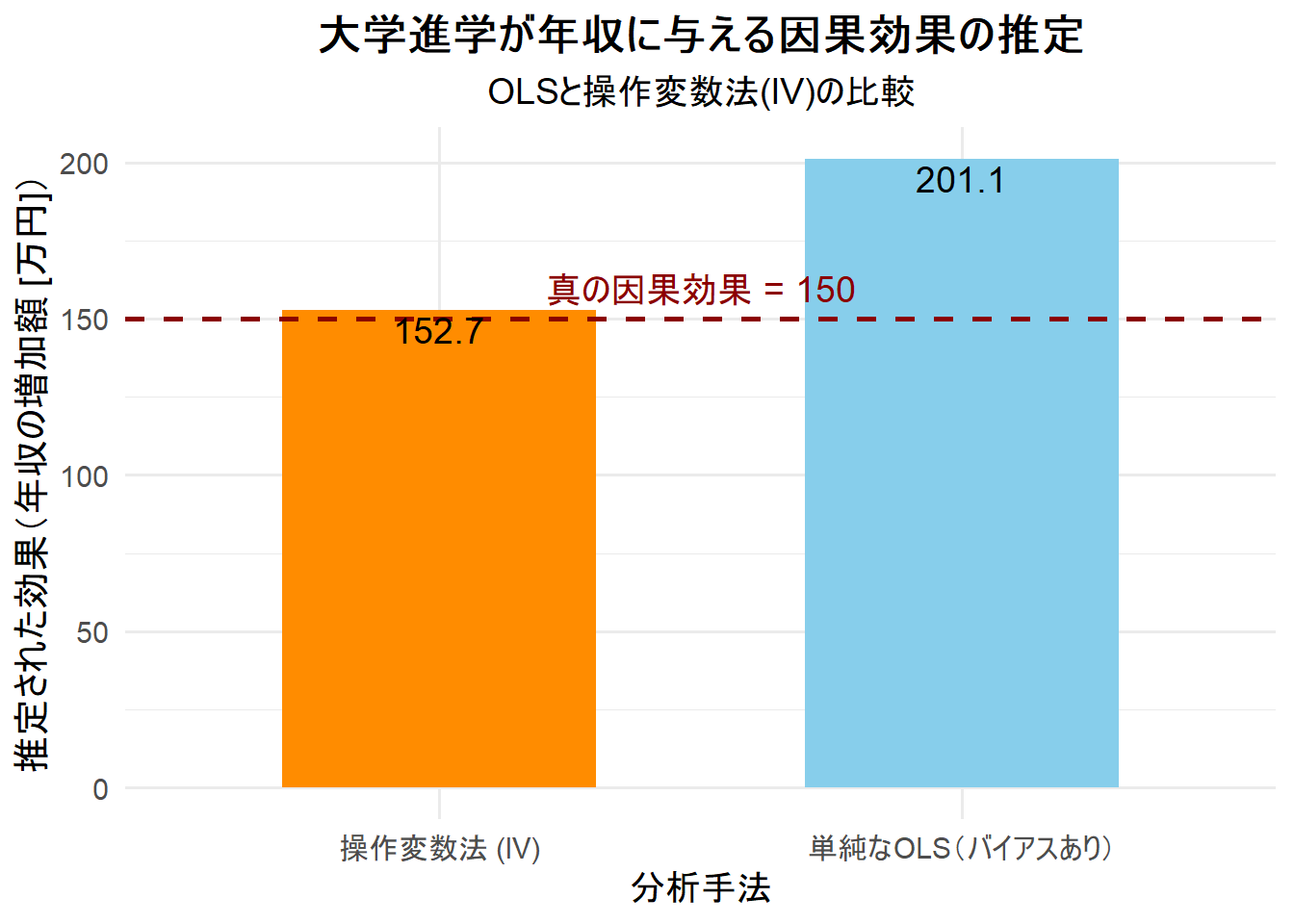
3.4. 結果の可視化
OLSとIVによる推定結果を棒グラフで比較してみましょう。
# 結果をまとめたデータフレームを作成
results_df <- tibble(
Method = c("単純なOLS(バイアスあり)", "操作変数法 (IV)"),
Estimate = c(coef(model_ols)[2], coef(model_iv)[2])
)
# 棒グラフで結果を比較
ggplot(results_df, aes(x = Method, y = Estimate, fill = Method)) +
geom_col(width = 0.6) +
geom_hline(
yintercept = beta_x,
linetype = "dashed",
color = "darkred",
linewidth = 1
) +
geom_text(
aes(label = round(Estimate, 1)),
vjust = 1.2,
size = 5
) +
annotate(
"text",
x = 1.5,
y = beta_x + 10,
label = paste("真の因果効果 =", beta_x),
color = "darkred",
size = 5
) +
scale_fill_manual(
values = c("単純なOLS(バイアスあり)" = "skyblue", "操作変数法 (IV)" = "darkorange")
) +
labs(
title = "大学進学が年収に与える因果効果の推定",
subtitle = "OLSと操作変数法(IV)の比較",
x = "分析手法",
y = "推定された効果(年収の増加額 [万円])"
) +
theme_minimal(base_size = 14) +
theme(
legend.position = "none",
plot.title = element_text(hjust = 0.5, face = "bold"),
plot.subtitle = element_text(hjust = 0.5)
)以上です。