Rの関数から prophet {prophet} を確認します。
1. prophet関数について
prophet関数は、prophetパッケージの中心となる関数で、時系列データから予測モデルを構築(学習)するために使用されます。この関数は、時系列データを入力として受け取り、トレンド、季節性、祝日効果などを考慮したモデルオブジェクトを返します。
prophetの主な特徴は以下の通りです。
- 自動化: トレンドの変化点や季節性を自動で検出します。
- 柔軟性: ドメイン知識(祝日、イベント、トレンドの変化など)をモデルに組み込むことができます。
- コンポーネント: モデルは以下の3つの主要なコンポーネントの加法モデル(または乗法モデル)で構成されています。
-
g(t): トレンド (Trend) – 区分的線形モデルまたは飽和状態を表現するロジスティックモデルで、非周期的な変化を捉えます。 -
s(t): 季節性 (Seasonality) – 年、週、日といった周期的な変動をフーリエ級数でモデル化します。 -
h(t): 祝日・イベント (Holidays) – 祝日やその他不規則なイベントが予測に与える影響をモデル化します。
-
- 不確実性の評価: ベイズ統計の枠組みに基づいており、予測値だけでなく、その不確実性を示す予測区間も算出できます。
prophet関数は、モデルの仕様を定義し、与えられたデータ(データフレーム)にモデルを適合させる(フィッティングする)役割を担います。
2. prophet関数の引数の説明
以下にprophet関数の引数を説明します。
args(prophet::prophet)function (df = NULL, growth = "linear", changepoints = NULL,
n.changepoints = 25, changepoint.range = 0.8, yearly.seasonality = "auto",
weekly.seasonality = "auto", daily.seasonality = "auto",
holidays = NULL, seasonality.mode = "additive", seasonality.prior.scale = 10,
holidays.prior.scale = 10, changepoint.prior.scale = 0.05,
mcmc.samples = 0, interval.width = 0.8, uncertainty.samples = 1000,
fit = TRUE, backend = NULL, ...)
NULL-
df: 学習に使用する時系列データを含むデータフレーム。以下の2つの列が必須です。-
ds: 日付または日時(Date型またはPOSIXct型)。 -
y: 予測対象の数値。
-
-
growth: トレンドのモデルを指定します。-
'linear': (デフォルト) 区分的線形トレンド。 -
'logistic': 飽和する成長(上限・下限がある場合)をモデル化するロジスティックトレンド。この場合、dfにcap(上限値)列が必要です。
-
-
changepoints: トレンドが変化する日付(変化点)をベクトルで手動で指定します。NULL(デフォルト)の場合、prophetが自動で設定します。 -
n.changepoints: 自動で設定するトレンド変化点の数。デフォルトは25です。 -
changepoint.range: トレンド変化点を設定する期間の範囲を、データ全体の先頭からの割合で指定します。デフォルトは0.8(データの最初の80%の期間)です。 -
yearly.seasonality: 年周期の季節性をモデルに含めるかどうか。'auto'(デフォルト),TRUE,FALSEから選択します。'auto'はデータ期間が1年以上あれば自動的にTRUEになります。 -
weekly.seasonality: 週周期の季節性をモデルに含めるかどうか。'auto'(デフォルト),TRUE,FALSEから選択します。'auto'はデータ期間が1週間以上あれば自動的にTRUEになります。 -
daily.seasonality: 日周期の季節性をモデルに含めるかどうか。'auto'(デフォルト),TRUE,FALSEから選択します。'auto'は時間単位のデータの場合に自動的にTRUEになります。 -
holidays: 祝日やイベントの効果をモデルに含めるためのデータフレーム。holiday(イベント名)とds(日付)の列が必要です。オプションでlower_windowとupper_windowを指定すると、イベントの前後数日間にも影響を広げることができます。 -
seasonality.mode: 季節性の効果をどのようにモデルに組み込むかを指定します。-
'additive': (デフォルト) 加法モデル。y(t) = g(t) + s(t) + h(t) + error -
'multiplicative': 乗法モデル。y(t) = g(t) * (1 + s(t) + h(t)) + error。季節性の変動がトレンドの大きさに比例する場合に有効です。
-
-
seasonality.prior.scale: 季節性モデルの柔軟性を調整するパラメータ。値が大きいほど、季節性の変動がデータに強く適合し、振幅が大きくなる傾向があります。デフォルトは10。 -
holidays.prior.scale: 祝日モデルの柔軟性を調整するパラメータ。値が大きいほど、祝日の効果がデータに強く適合します。デフォルトは10。 -
changepoint.prior.scale: トレンド変化点の柔軟性を調整するパラメータ。値が大きいほど、トレンドの変化が大きくなり、データに追従しやすくなります(過学習のリスク増)。小さいほどトレンドは滑らかになります。デフォルトは0.05。 -
mcmc.samples: MCMC(マルコフ連鎖モンテカルロ法)サンプリングを実行する回数。デフォルトは0で、この場合はMAP(最大事後確率)推定によりパラメータが決定されます。0より大きい値を設定すると、パラメータの不確実性をより詳細に評価できますが、計算に時間がかかります。 -
interval.width: 予測区間の幅。デフォルトは0.8(80%予測区間)。 -
uncertainty.samples: 予測区間を計算するためのシミュレーション回数。デフォルトは1000。 -
fit:TRUE(デフォルト)の場合、prophetオブジェクトの作成と同時にモデルの学習を実行します。 -
backend: Stanのバックエンドを指定します(例: ‘rstan’, ‘cmdstanr’)。 -
...: Stanの最適化関数(optimizing)またはサンプリング関数(sampling)に渡す追加の引数。
get_stan_backend()の選択ロジック
if (is.null(backend))
backend <- get_stan_backend()backend引数がNULL(デフォルトの状態)の場合、prophetパッケージの内部関数であるget_stan_backend()が呼び出され、その返り値がバックエンドとして使用されます。
get_stan_backend()関数は、以下の優先順位に従って使用するStanバックエンドを自動的に決定します。
グローバルオプションの確認: まず、Rのグローバルオプションに
options('prophet.backend')が設定されているかを確認します。もしユーザーがoptions(prophet.backend = 'rstan')のように事前に設定していれば、その値が最優先で使われます。cmdstanrの確認: グローバルオプションが設定されていない場合、次にcmdstanrパッケージがインストールされているかをチェックします。もしインストールされていれば、'cmdstanr'がバックエンドとして選択されます。rstanの確認:cmdstanrがインストールされていない場合、次にrstanパッケージがインストールされているかをチェックします。もしインストールされていれば、'rstan'がバックエンドとして選択されます。どちらも無い場合:
cmdstanrとrstanのどちらもインストールされていない場合、エラーが発生し、どちらかのパッケージをインストールするように促すメッセージが表示されます。
| 状況 | 選択されるバックエンド |
|---|---|
cmdstanrとrstanの両方がインストールされている | cmdstanr (優先) |
cmdstanrのみがインストールされている | cmdstanr |
rstanのみがインストールされている | rstan |
| どちらもインストールされていない | エラー |
options(prophet.backend = 'rstan') が設定されている場合 | rstan (最優先) |
結論として、backend引数がNULLの場合、cmdstanrがインストールされていればcmdstanrが、されていなければrstanが自動的に選択されます。
現在の環境でどちらが使われるか確認する方法
以下のコードを実行することで、自身の環境でprophetがデフォルトでどちらのバックエンドを使用するかを確認できます。
cat("パッケージrstanを確認:\n")
"rstan" %in% installed.packages()[, "Package"]
cat("\nパッケージcmdstanrを確認:\n")
"cmdstanr" %in% installed.packages()[, "Package"]
# prophetの内部関数get_stan_backendを呼び出して確認
# ::: を使うことで、パッケージの内部関数にアクセスできます
cat("\n現在の環境でデフォルトで選択されるStanバックエンド:\n")
prophet:::get_stan_backend()
# もし'cmdstanr'と'rstan'の両方がインストールされている環境で、
# あえて'rstan'を使いたい場合は、以下のようにオプションを設定します。
# options(prophet.backend = 'rstan')
# cat("\nオプション設定後に選択されるStanバックエンド:\n")
# prophet:::get_stan_backend()
# options(prophet.backend = NULL) # 確認後に設定を元に戻すパッケージrstanを確認:
[1] TRUE
パッケージcmdstanrを確認:
[1] FALSE
現在の環境でデフォルトで選択されるStanバックエンド:
[1] "rstan"3. サンプルデータの作成
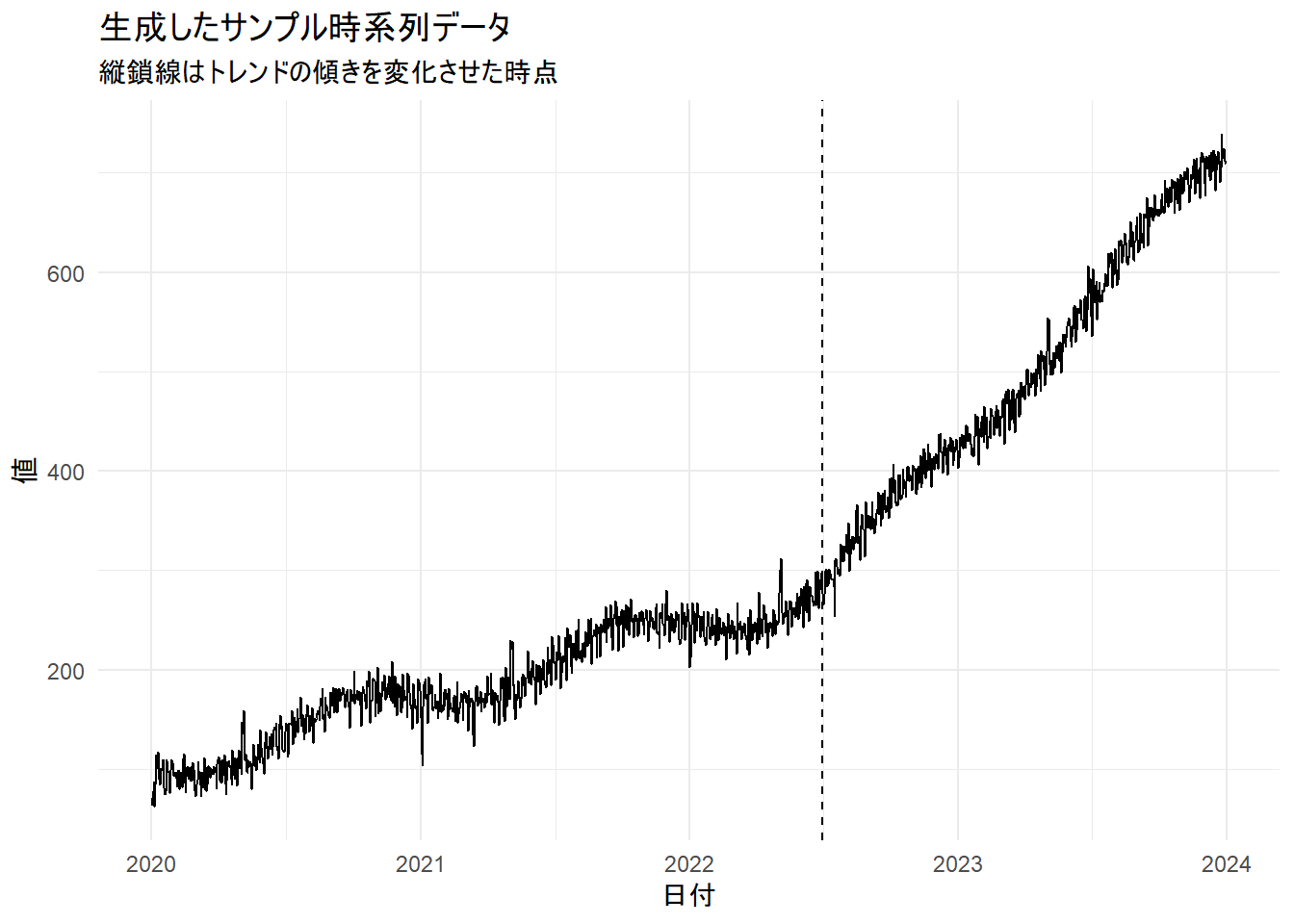
シミュレーションのために、トレンド、年・週周期の季節性、祝日効果を含むサンプル時系列データを作成します。
# 必要なパッケージをロード
library(prophet)
library(dplyr)
library(ggplot2)
options(scipen = 999)
# 再現性のための乱数シード設定
seed <- 20250915
set.seed(seed)
# 1. データ期間の設定 (2020年1月1日 から 2023年12月31日)
ds <- seq(as.Date("2020-01-01"), as.Date("2023-12-31"), by = "day")
n <- length(ds)
# 2. 各コンポーネントの生成
# 2-1. トレンド成分 (2022年7月1日に傾きが変わる)
t1 <- 1:n
t2 <- pmax(0, t1 - which(ds == as.Date("2022-07-01")))
trend <- 100 + 0.2 * t1 + 0.6 * t2
# 2-2. 季節性成分 (年周期と週周期)
yearly_seasonality <- 20 * sin(2 * pi * (as.numeric(format(ds, "%j")) / 365.25 - 0.5))
weekly_seasonality <- 10 * case_when(
weekdays(ds) == "土曜日" ~ -1,
weekdays(ds) == "日曜日" ~ -1.5,
TRUE ~ 0.2
)
# 2-3. 祝日効果データフレームの作成 (正月とゴールデンウィーク)
holidays_df <- bind_rows(
data.frame(holiday = "正月", ds = as.Date(paste0(2020:2024, "-01-01"))),
data.frame(holiday = "正月", ds = as.Date(paste0(2020:2024, "-01-02"))),
data.frame(holiday = "正月", ds = as.Date(paste0(2020:2024, "-01-03"))),
data.frame(holiday = "GW", ds = as.Date(paste0(2020:2024, "-05-03"))),
data.frame(holiday = "GW", ds = as.Date(paste0(2020:2024, "-05-04"))),
data.frame(holiday = "GW", ds = as.Date(paste0(2020:2024, "-05-05")))
)
holiday_effect <- ifelse(ds %in% holidays_df$ds[holidays_df$holiday == "正月"], -30, 0) +
ifelse(ds %in% holidays_df$ds[holidays_df$holiday == "GW"], 40, 0)
# 2-4. ノイズ成分
noise <- rnorm(n, mean = 0, sd = 10)
# 3. yの値を合成
y <- trend + yearly_seasonality + weekly_seasonality + holiday_effect + noise
# 4. prophet用のデータフレームを作成
df <- data.frame(ds, y)
# 5. データの可視化
cat("作成したサンプルデータの一部を確認:\n")
print(head(df))
p <- ggplot(df, aes(x = ds, y = y)) +
geom_line() +
labs(title = "生成したサンプル時系列データ", subtitle = "縦鎖線はトレンドの傾きを変化させた時点", x = "日付", y = "値") +
theme_minimal() +
geom_vline(xintercept = as.Date("2022-07-01"), linetype = "dashed")
print(p)作成したサンプルデータの一部を確認:
ds y
1 2020-01-01 63.12112
2 2020-01-02 71.52465
3 2020-01-03 77.72553
4 2020-01-04 87.11572
5 2020-01-05 61.89076
6 2020-01-06 84.326744. prophet関数を用いたシミュレーション
作成したサンプルデータを用いて、prophet関数の主要な引数を変更しながら、その効果を確認します。
シミュレーション1: 基本的な予測
まず、デフォルト設定でprophetを動かしてみます。
よって、changepoint.prior.scale = 0.05 となります。
# 1. prophetモデルの学習
# デフォルトの引数を変更せず、prophetに自動でモデルを構築させます
m1 <- prophet(df)
# 2. 未来のデータフレームを作成 (365日分)
future1 <- make_future_dataframe(m1, periods = 365)
cat("作成した未来のデータフレームの最後の部分:\n")
print(tail(future1))
# 3. 予測の実行
forecast1 <- predict(m1, future1)
cat("\n予測結果のデータフレームの主要な列:\n")
print(head(forecast1[c("ds", "yhat", "yhat_lower", "yhat_upper")]))
# 4. 予測結果のプロット
p_forecast1 <- plot(m1, forecast1) +
add_changepoints_to_plot(m1) + # 変化点をプロット
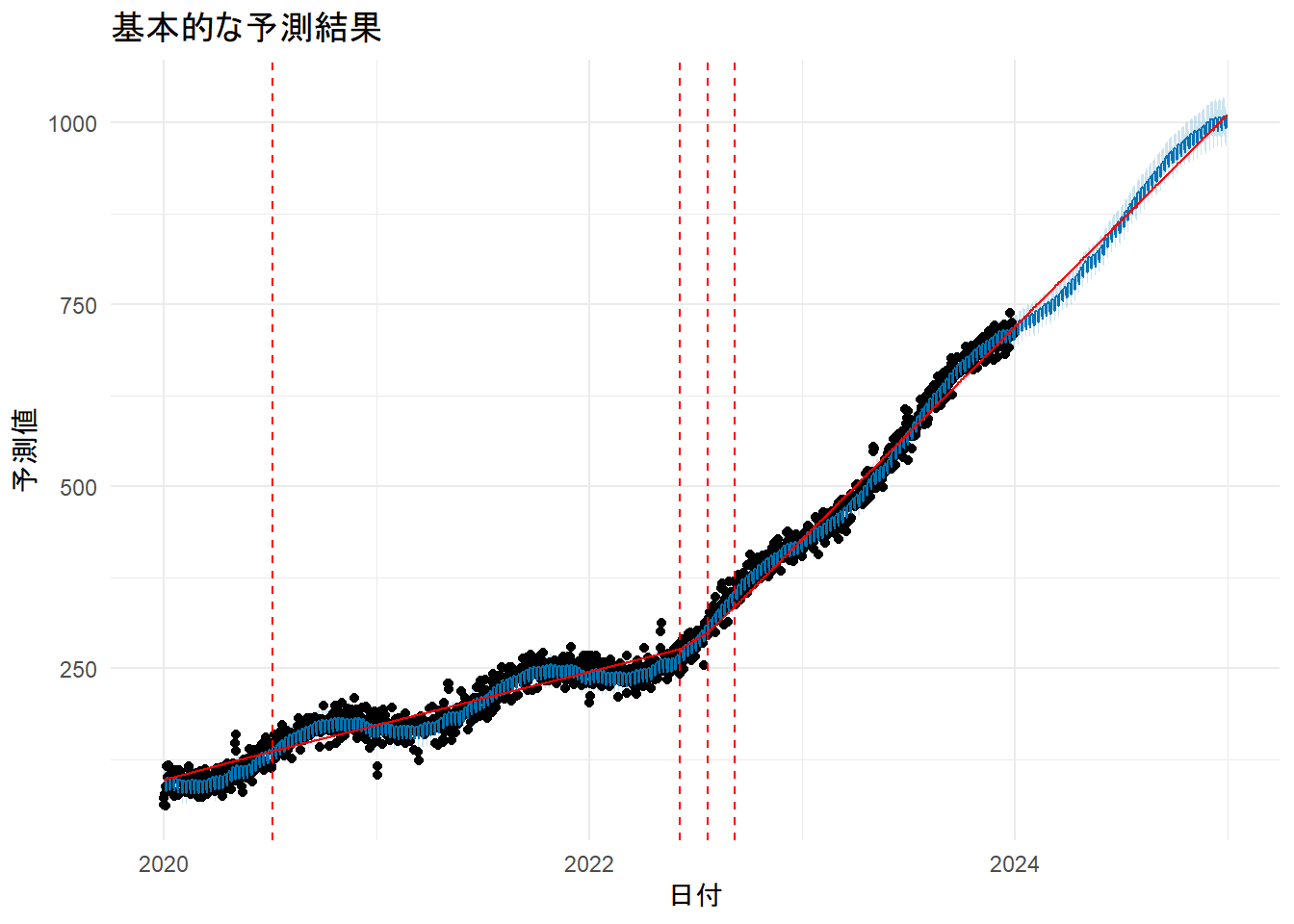
labs(title = "基本的な予測結果", x = "日付", y = "予測値") +
theme_minimal()
print(p_forecast1)
# 5. 成分のプロット
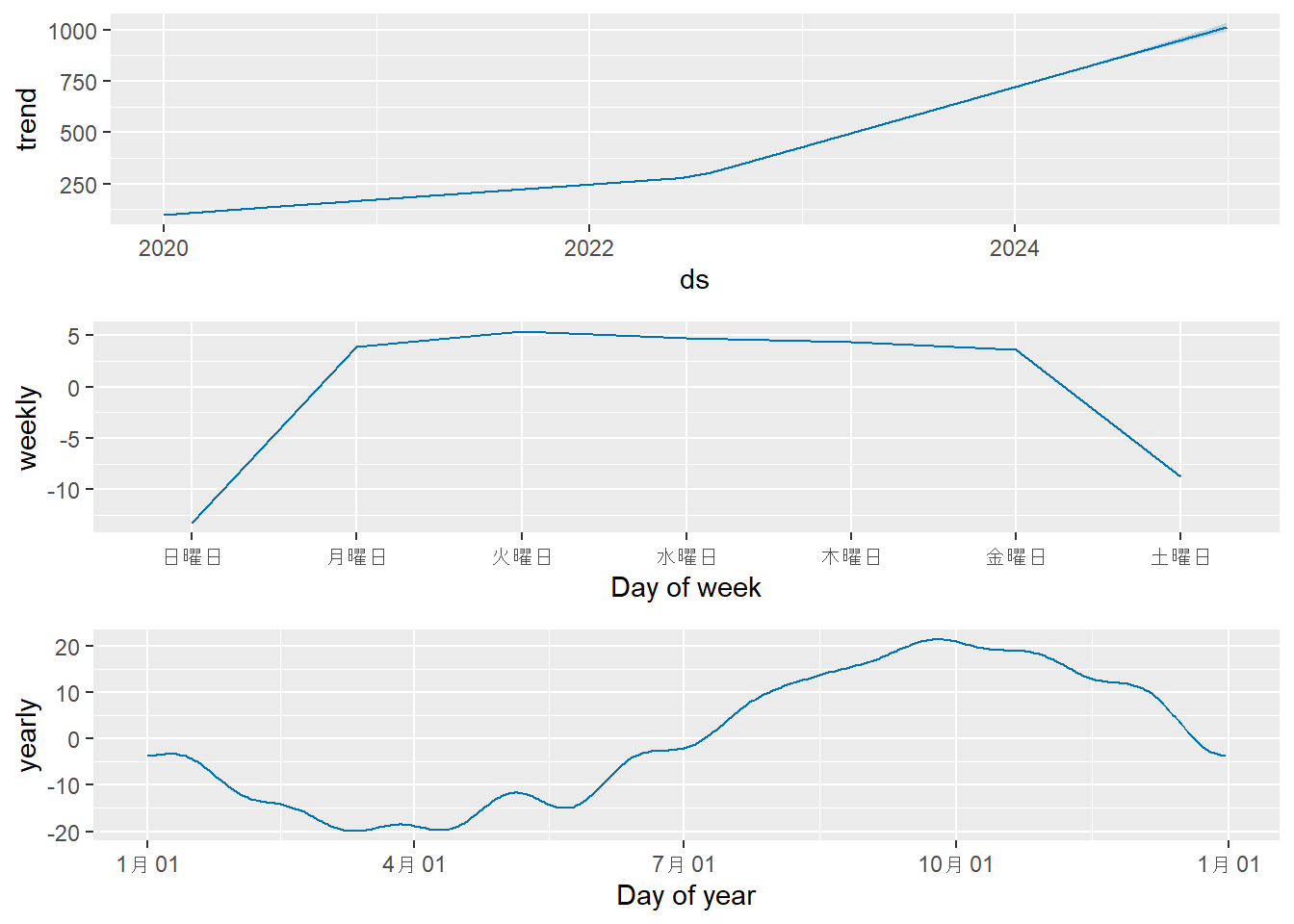
cat("モデルの各成分(トレンド、週周期、年周期)を可視化します。\n")
prophet_plot_components(m1, forecast1)作成した未来のデータフレームの最後の部分:
ds
1821 2024-12-25
1822 2024-12-26
1823 2024-12-27
1824 2024-12-28
1825 2024-12-29
1826 2024-12-30
予測結果のデータフレームの主要な列:
ds yhat yhat_lower yhat_upper
1 2020-01-01 97.71500 84.86831 112.83081
2 2020-01-02 97.56777 82.76330 111.38134
3 2020-01-03 96.99201 81.38622 111.92270
4 2020-01-04 84.92256 71.10136 100.02579
5 2020-01-05 80.68583 67.09892 95.17141
6 2020-01-06 98.18674 83.38920 112.25342
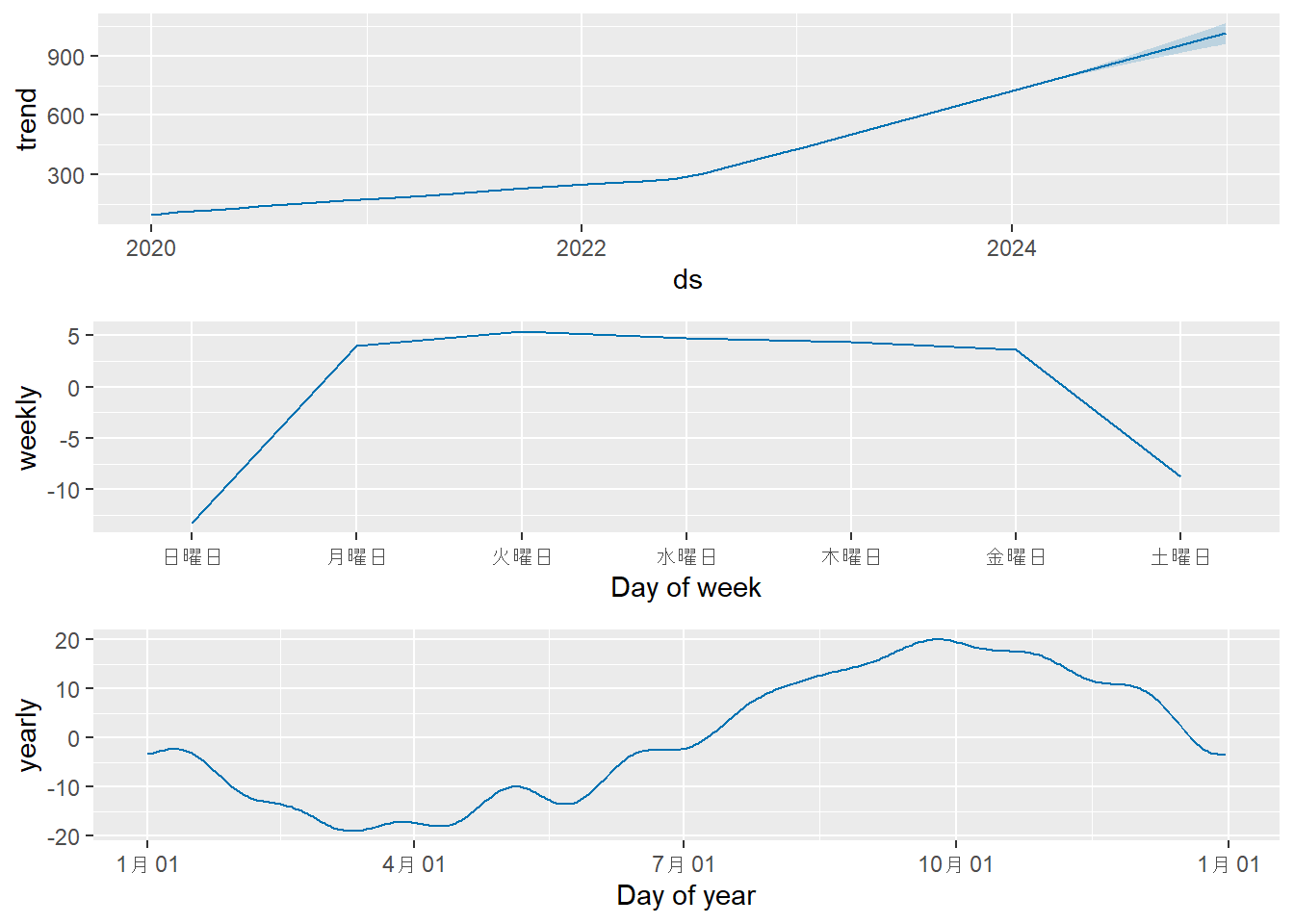
モデルの各成分(トレンド、週周期、年周期)を可視化します。解説:`
- Figure 2 の黒い点 (
y): 実際の観測値データです。これが元データとなります。 - Figure 2 の赤色の実線 (
trend): データから学習した長期的な傾向です。季節性などの周期的な変動はここから取り除かれています。 - Figure 2 の青色の実線 (
yhat): モデルによる最終的な予測値です。これは、トレンド成分に季節性や祝日効果などをすべて足し合わせたものになります (yhat = trend + seasonality + holiday_effects)。そのため、青い線は赤い線(トレンド)の周りを周期的に振動するような形になります。 - 赤色の縦の破線 (
changepoints): トレンドの傾きが変化する可能性のある変化点です。 - Figure 2 の青色の実線を見ますと、データ全体の大まかな傾向と周期性を捉えられていることがわかります。
- Figure 3 の成分プロットでは、モデルが学習した トレンド(2022年7月1日を境に傾きが急になる)、週周期(土日に値が下がる)、年周期(sinカーブ)のパターンを確認できます。
シミュレーション2: トレンド変化点の柔軟性を調整 (changepoint.prior.scale)
この引数は、トレンドがどの程度データに追従するかを制御します。changepoint.prior.scaleが小さいとトレンドは直線に近くなり(未学習のリスク)、大きいとデータに過剰に追従します(過学習のリスク)。
# changepoint.prior.scale を意図的に小さく設定(未学習)
changepoint.prior.scale.low <- 0.0005
m2_low_cps <- prophet(df, changepoint.prior.scale = changepoint.prior.scale.low)
forecast2_low_cps <- predict(m2_low_cps, future1)
# changepoint.prior.scale を意図的に大きく設定(過学習)
changepoint.prior.scale.high <- 1
m2_high_cps <- prophet(df, changepoint.prior.scale = changepoint.prior.scale.high)
forecast2_high_cps <- predict(m2_high_cps, future1)
# プロットして比較
p_trend_comp <- plot(m2_low_cps, forecast2_low_cps) +
add_changepoints_to_plot(m2_low_cps) + # 変化点をプロット
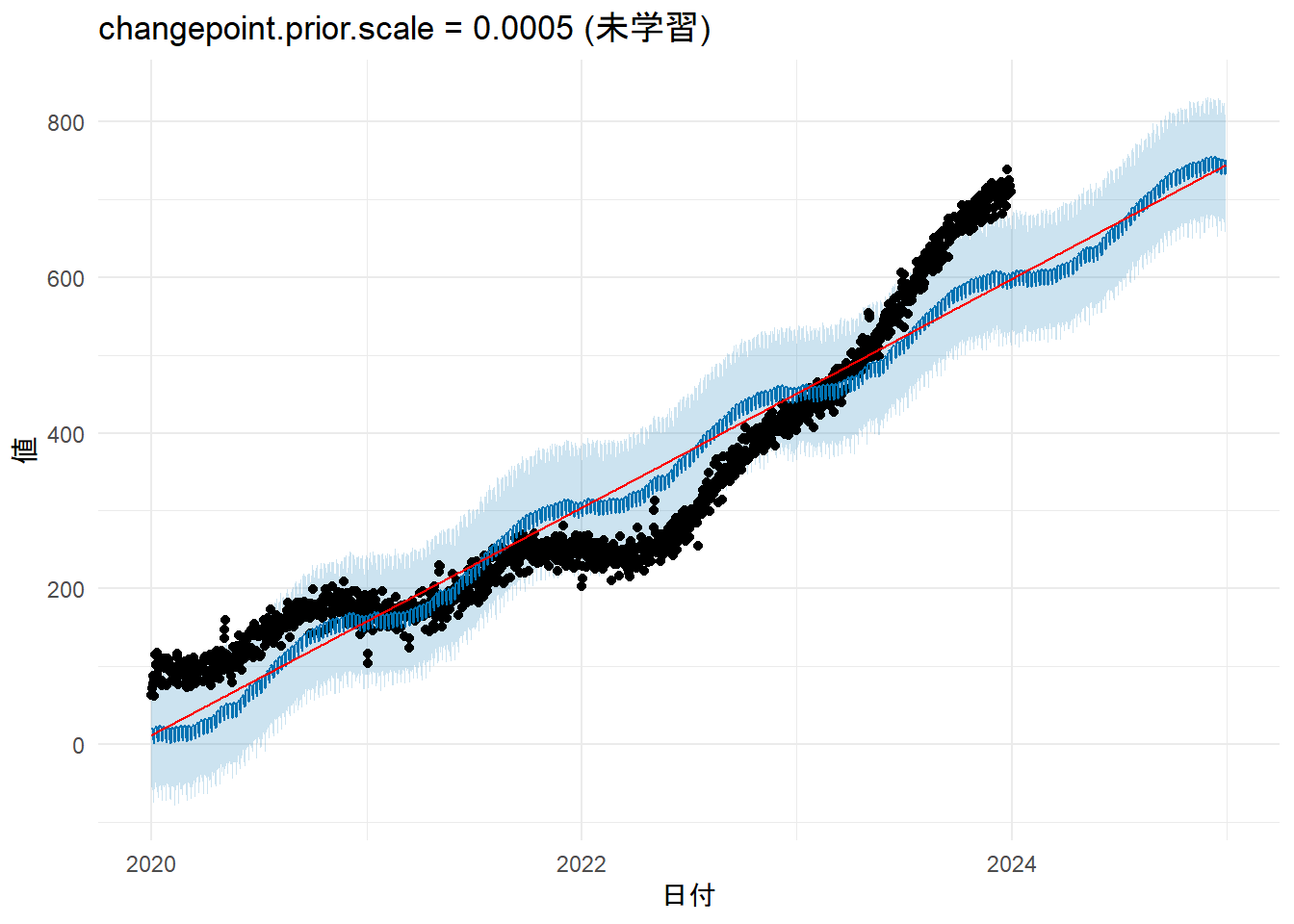
labs(title = paste0("changepoint.prior.scale = ", changepoint.prior.scale.low, " (未学習)"), x = "日付", y = "値") + theme_minimal()
print(p_trend_comp)
prophet_plot_components(m2_low_cps, forecast2_low_cps)
p_trend_comp2 <- plot(m2_high_cps, forecast2_high_cps) +
add_changepoints_to_plot(m2_high_cps) +
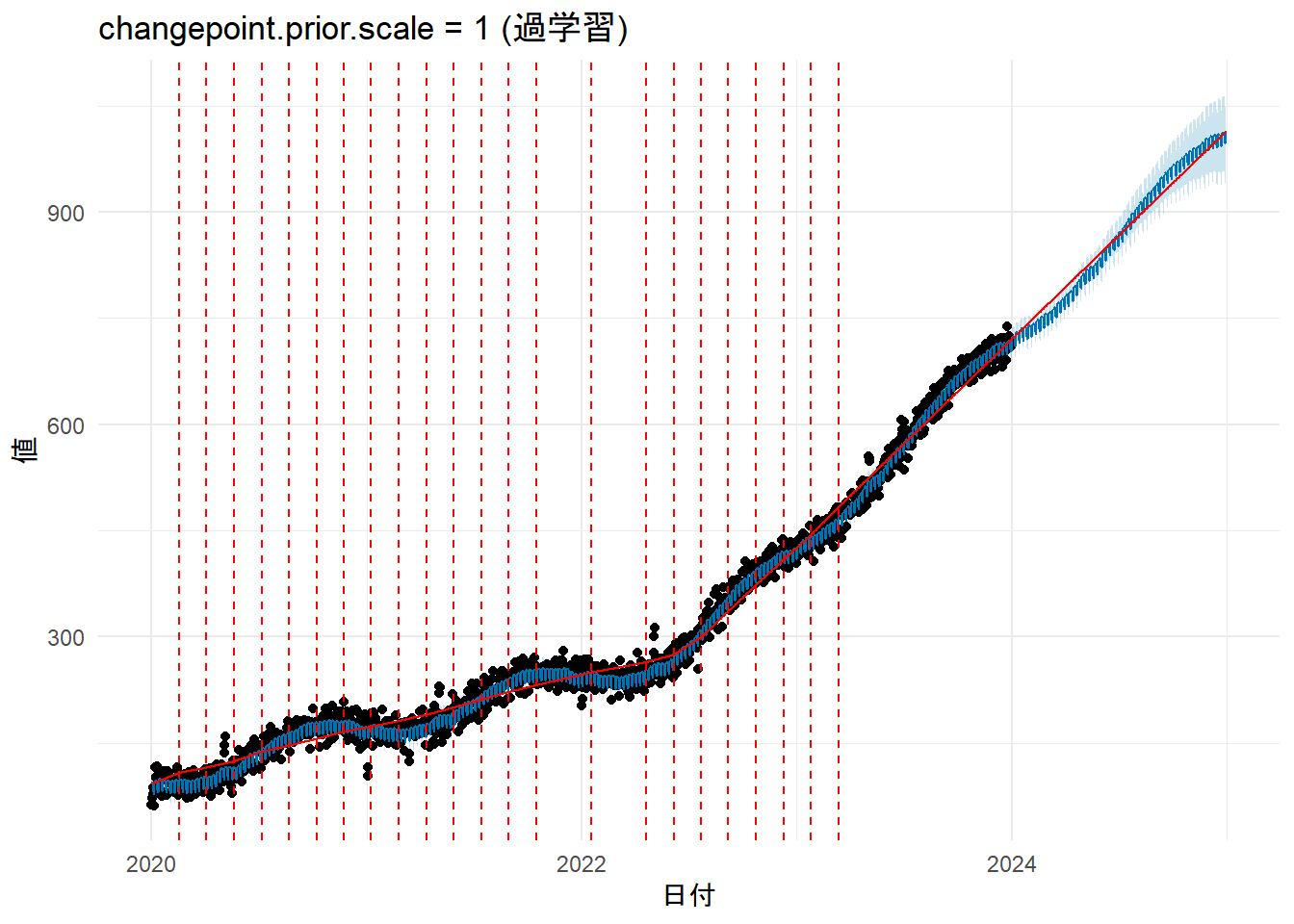
labs(title = paste0("changepoint.prior.scale = ", changepoint.prior.scale.high, " (過学習)"), x = "日付", y = "値") + theme_minimal()
print(p_trend_comp2)
prophet_plot_components(m2_high_cps, forecast2_high_cps)解説:`
- Figure 4 と Figure 6 を比較しますと、
prophetがモデルの学習時に設定したトレンド変化点(changepoints)(赤色縦鎖線)が異なっていることが確認できます。 -
prophetは、トレンドを一本の直線ではなく、複数の直線を繋ぎ合わせた区分的線形モデルとして捉えます。トレンド変化点とは、その直線の傾きが変わることを許容するポイントのことです。 - デフォルトでは学習データの最初の80%の期間に、25個のトレンド変化点を等間隔で自動的に配置します。赤色縦破線は、これらの「傾きが変化するかもしれない候補地点」の場所を表しています。
-
changepoint.prior.scale引数は、これらの各変化点で実際にどの程度傾きを変化させるかを制御するパラメータです。 - Figure 4 は
changepoint.prior.scaleを意図的に小さくしましたので、傾きの変化が強く抑制(正則化)され、トレンド変化点は設定されず、トレンドラインは直線になっています。 - Figure 6 は
changepoint.prior.scaleを意図的に大きくしましたので、傾きの変化に対する制約が緩くなり、画像では判別しにくいのですが、トレンドラインは各トレンド変化点でうねっています。
トレンドの傾きの変化量(delta)の確認:`
args(prophet:::add_changepoints_to_plot)function (m, threshold = 0.01, cp_color = "red", cp_linetype = "dashed",
trend = TRUE, ...)
NULLデフォルトの閾値は threshold = 0.01 です。
cat(paste0("--- changepoint.prior.scale = ", changepoint.prior.scale.low, " の場合 (未学習) ---\n"))
cat("学習された傾きの変化量 (delta):\n")
m2_low_cps$params$delta %>% as.vector()
cat("閾値以上の変化量の数:\n")
m2_low_cps$params$delta %>%
as.vector() %>%
{
abs(.) > 0.01
} %>%
sum()
cat(paste0("\n--- changepoint.prior.scale = ", changepoint.prior.scale.high, " の場合 (過学習) ---\n"))
cat("学習された傾きの変化量 (delta):\n")
m2_high_cps$params$delta %>% as.vector()
cat("閾値以上の変化量の数:\n")
m2_high_cps$params$delta %>%
as.vector() %>%
{
abs(.) > 0.01
} %>%
sum()--- changepoint.prior.scale = 0.0005 の場合 (未学習) ---
学習された傾きの変化量 (delta):
[1] -0.0000000102287771 -0.0000000052741347 0.0000000090185443 -0.0000000127168979 0.0000000093902070 0.0000000067743621 0.0000000170737477 0.0000000081196290 0.0000000025423889
[10] -0.0000000106257689 0.0000000154860468 0.0000000078525166 -0.0000000006202806 0.0000000235968450 0.0000001399429490 0.0000000574850604 0.0000003464482651 0.0055475075252278
[19] 0.0000377904075615 0.0000000079672844 0.0000000340949224 0.0000000079441528 0.0000000118084796 0.0000000081132075 0.0000000011653391
閾値以上の変化量の数:
[1] 0
--- changepoint.prior.scale = 1 の場合 (過学習) ---
学習された傾きの変化量 (delta):
[1] -0.34089973700 0.06148854502 0.20342526821 -0.20725112388 0.02254244374 0.02858611058 -0.11186707358 0.02824914420 0.02811396363 0.06979932594 0.03523021631 -0.01029346242 -0.05891860050
[14] -0.02658849419 0.00004802572 -0.06757982715 -0.00346437411 0.15103887329 0.60984174226 0.50907432050 -0.01334631775 -0.04535574429 -0.05278503192 0.20495859883 -0.07489827355
閾値以上の変化量の数:
[1] 23- 意図的に
changepoint.prior.scaleを小さくした未学習のケースでは、閾値以上の変化量の数はゼロですので Figure 4 にはトレンド変化点が現れていません。 - 過学習のケースでは閾値以上の変化量の数は23ですので Figure 6 には23本の赤色縦鎖線が現れています。
シミュレーション3: 祝日効果の追加 (holidays)
次に、作成しておいた祝日データフレームをモデルに組み込みます。
正月とGWの情報を祝日としてモデルに与えます。
成分プロットに holidays が追加され、各祝日の効果が可視化されます。
# holidays引数に祝日データフレームを渡す
m3_holidays <- prophet(df, holidays = holidays_df)
forecast3_holidays <- predict(m3_holidays, future1)
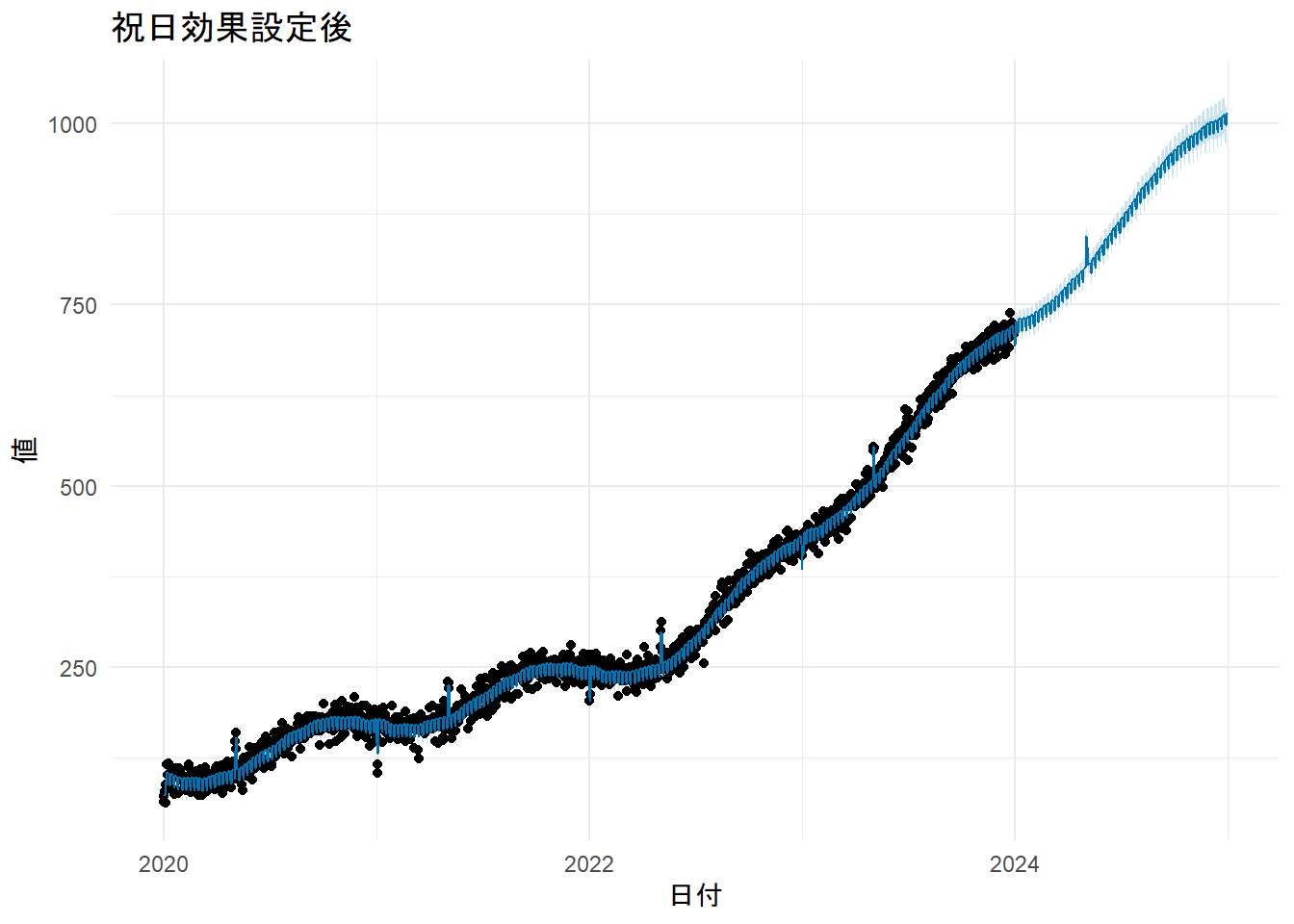
p_holiday <- plot(m3_holidays, forecast3_holidays) +
labs(title = "祝日効果設定後", x = "日付", y = "値") + theme_minimal()
print(p_holiday)
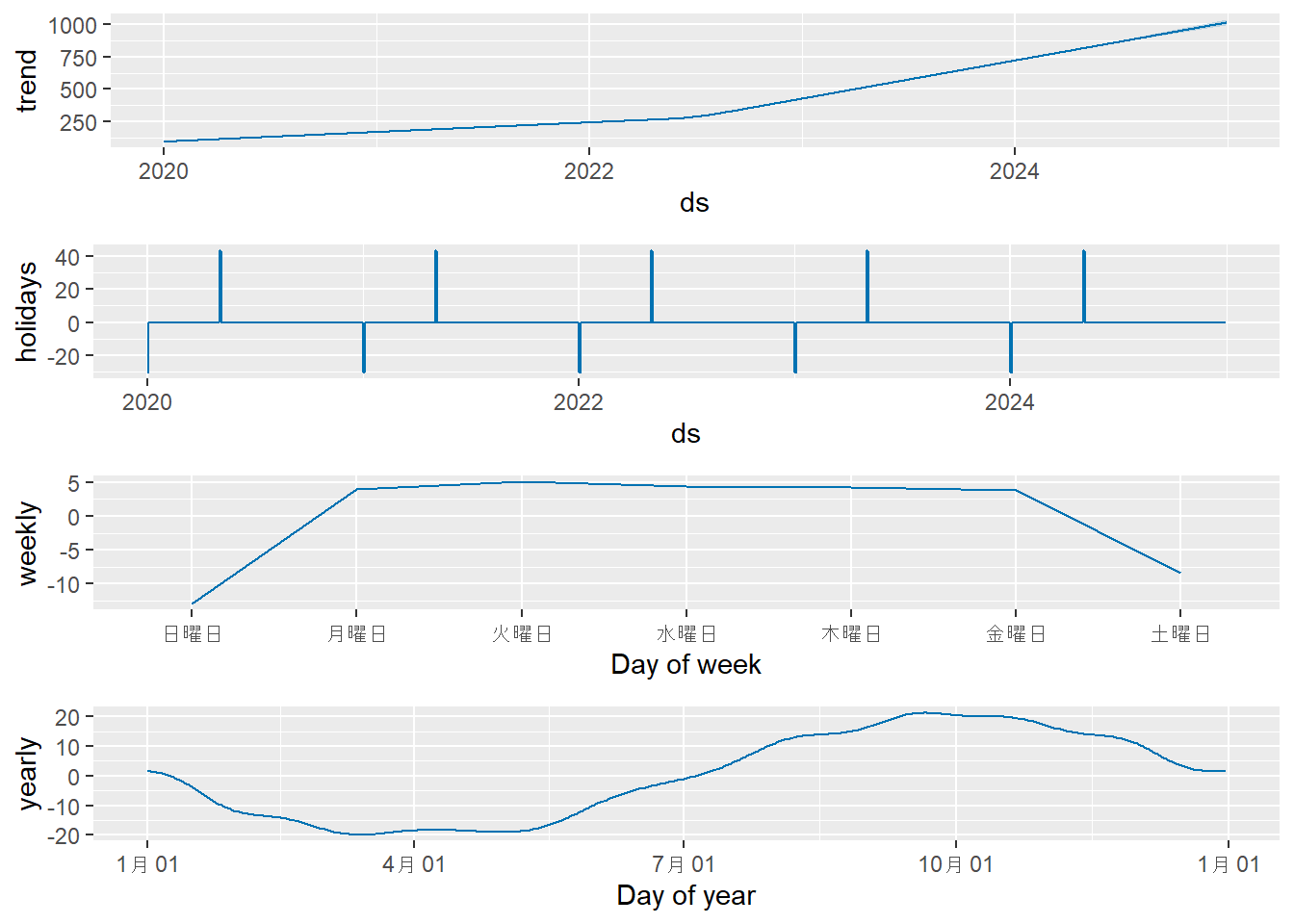
prophet_plot_components(m3_holidays, forecast3_holidays)解説:
- Figure 9 の成分プロットに
holidaysの項目が追加されました。モデルは「正月」には値が下がり(約-30)、「GW」には値が上がる(約+40)という効果を正しく学習しています。これにより、特定のイベントによる予測値の急な変動を説明でき、予測精度の向上が期待できます。
シミュレーション4: 季節性のモードを変更 (seasonality.mode)
デフォルトの加法モデル (additive) から乗法モデル (multiplicative) に変更してみましょう。乗法モデルは、季節性の変動がトレンドの大きさに比例するようなデータに適しています。
乗法モデルでは、季節性の効果が割合(%)で表現されます。
例えば、年周期の効果が0.1の場合、トレンドの10%分だけ値が上昇することを意味します。
# seasonality.modeを 'multiplicative' に設定
# 注意: 乗法モデルはy > 0を仮定するため、データによってはエラーになる場合があります
# 今回のサンプルデータは常に正なので問題ありません。
m4_multi <- prophet(df, seasonality.mode = "multiplicative", holidays = holidays_df)
forecast4_multi <- predict(m4_multi, future1)
p_multi <- plot(m4_multi, forecast4_multi) +
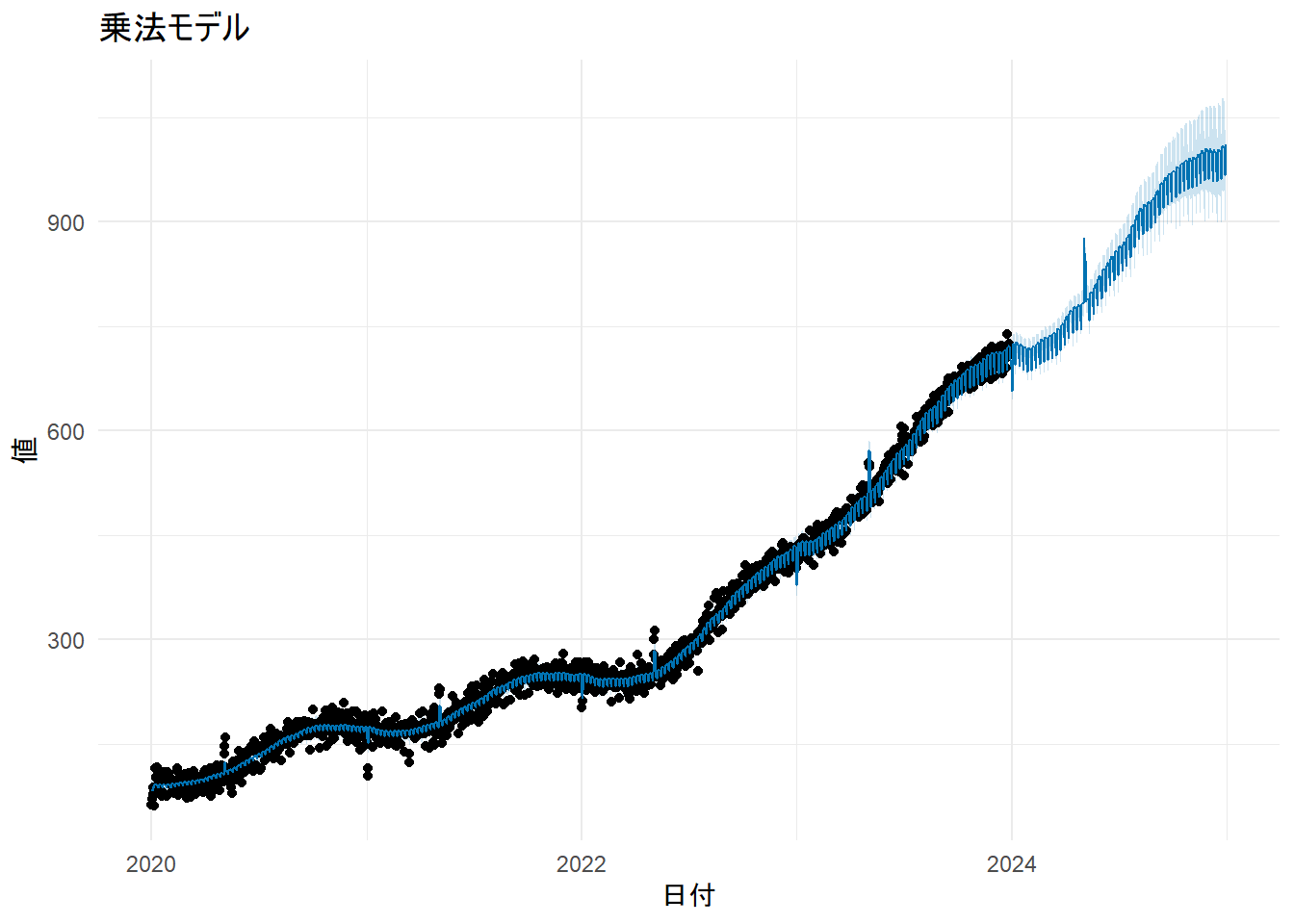
labs(title = "乗法モデル", x = "日付", y = "値") + theme_minimal()
print(p_multi)
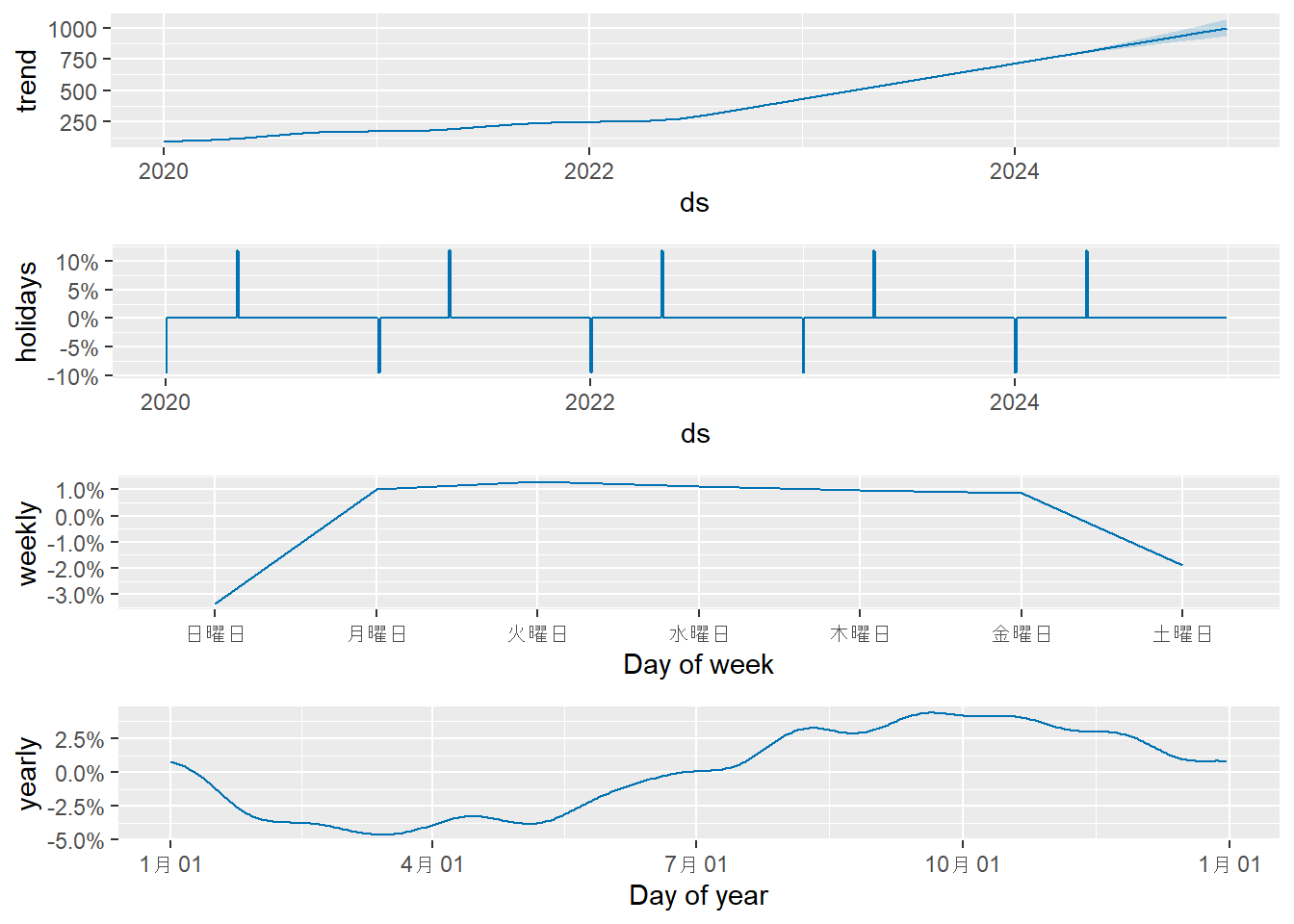
prophet_plot_components(m4_multi, forecast4_multi)解説:
- Figure 11 の成分プロットの縦軸が割合に変わっていることがわかります。
- 例えば、年周期のグラフを見ると、10月頃にはトレンドの約4%ほど値が上乗せされ、4月頃には約5%ほど値が下がるというパターンを学習しています。
- トレンドが上昇するにつれて季節変動の絶対額も大きくなるようなデータ(例:売上データ)の場合、乗法モデルがより適していることがあります。
5. 日周期のあるデータ
これまでのシミュレーションでは日次データをサンプルとしましたので、1日の中での周期的な変動(日周期)は考慮されませんでした。このセクションでは、1時間ごとのデータを作成し、prophetがどのように日周期を自動的に検出し、モデルに組み込むかを確認します。
まず、1か月分の時間単位のサンプルデータを作成します。このデータには、緩やかな上昇トレンド、週末に値が下がる週周期、そして1日の中で午前中に値が低く午後に高くなるという日周期が含まれています。
この時間単位のデータをprophet関数に渡しますと、データの間隔から日周期が存在する可能性を自動で判断し、モデルにdaily成分を追加します。
モデル学習後の成分プロットを見ることで、prophetがデータからどのような日周期パターンを学習したかを視覚的に確認できます。
set.seed(seed)
# 1. 日周期を含むサンプルデータ(時間単位)の作成
# 2023年1月1日から1月31日までの1時間ごとのデータ
ds_hourly <- seq(
from = as.POSIXct("2023-01-01 00:00:00", tz = "Asia/Tokyo"),
to = as.POSIXct("2023-01-31 23:00:00", tz = "Asia/Tokyo"),
by = "hour"
)
n_hourly <- length(ds_hourly)
# トレンド、週周期、日周期、ノイズを生成
trend_hourly <- 100 + 0.02 * (1:n_hourly)
# 週末は下がる週周期
weekly_seasonality_hourly <- 10 * ifelse(weekdays(ds_hourly) %in% c("土曜日", "日曜日"), -1.5, 0.2)
# 午後3時(15時)頃にピークを迎え、午前3時頃に底になる日周期
daily_seasonality_hourly <- 20 * sin(2 * pi * (as.numeric(format(ds_hourly, "%H")) - 9) / 24)
noise_hourly <- rnorm(n_hourly, mean = 0, sd = 5)
# 全てを合成
y_hourly <- trend_hourly + weekly_seasonality_hourly + daily_seasonality_hourly + noise_hourly
df_hourly <- data.frame(ds = ds_hourly, y = y_hourly)
cat("作成した時間単位データの一部を確認:\n")
print(head(df_hourly))
# 2. prophetモデルの学習
# 時間単位データを渡すと、日周期が自動で有効になります
m5_daily <- prophet(df_hourly)
# 3. 未来のデータフレームを作成 (7日分)
# freq='hour' を指定して時間単位で未来を生成
future5_daily <- make_future_dataframe(m5_daily, periods = 7 * 24, freq = "hour")
# 4. 予測の実行
forecast5_daily <- predict(m5_daily, future5_daily)
# 5. 予測結果のプロット(最後の10日間を拡大)
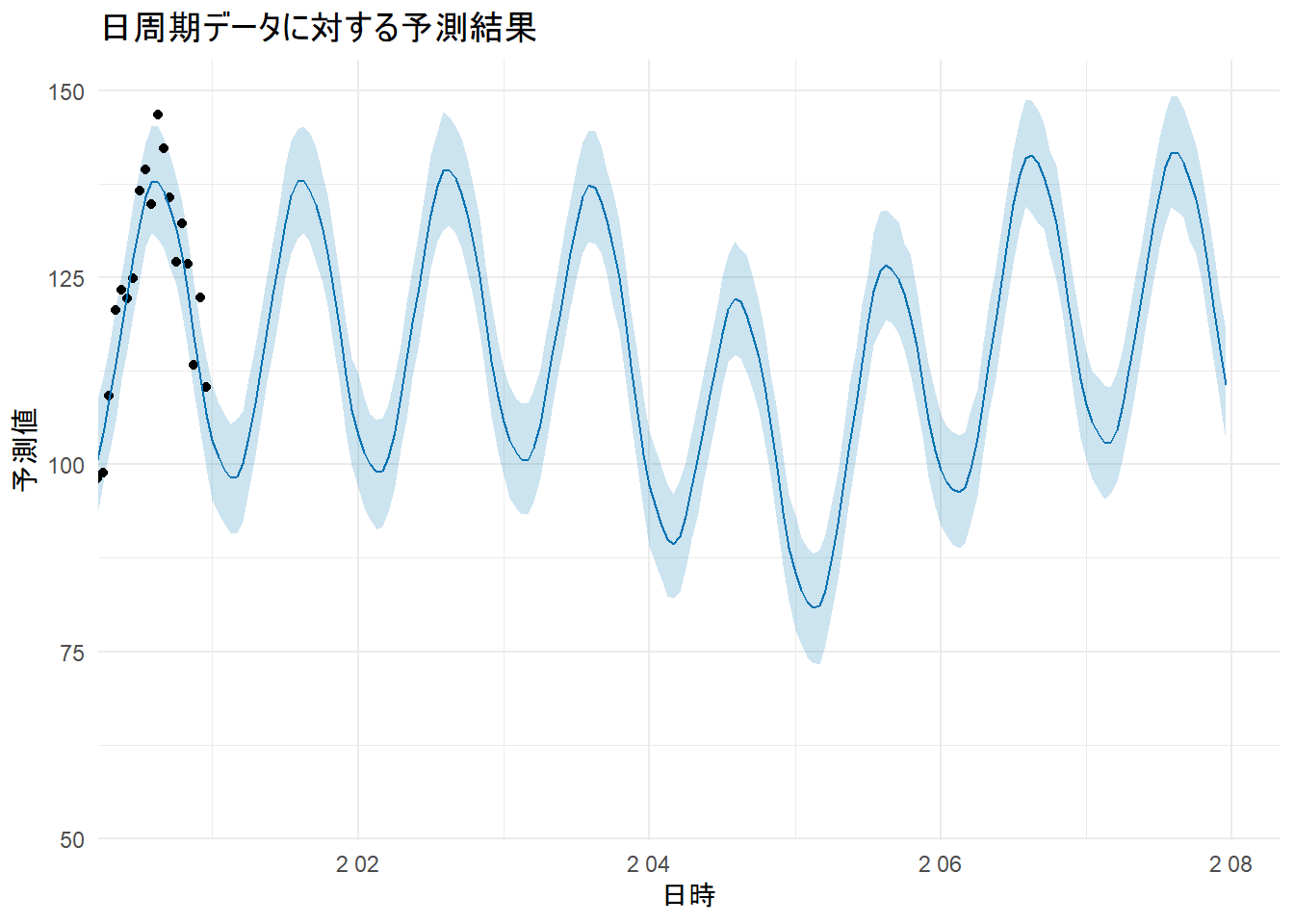
p_forecast5 <- plot(m5_daily, forecast5_daily) +
labs(title = "日周期データに対する予測結果", x = "日時", y = "予測値") +
coord_cartesian(xlim = c(max(df_hourly$ds) - 10, max(future5_daily$ds))) + # 最後の10日間にズーム
theme_minimal()
print(p_forecast5)
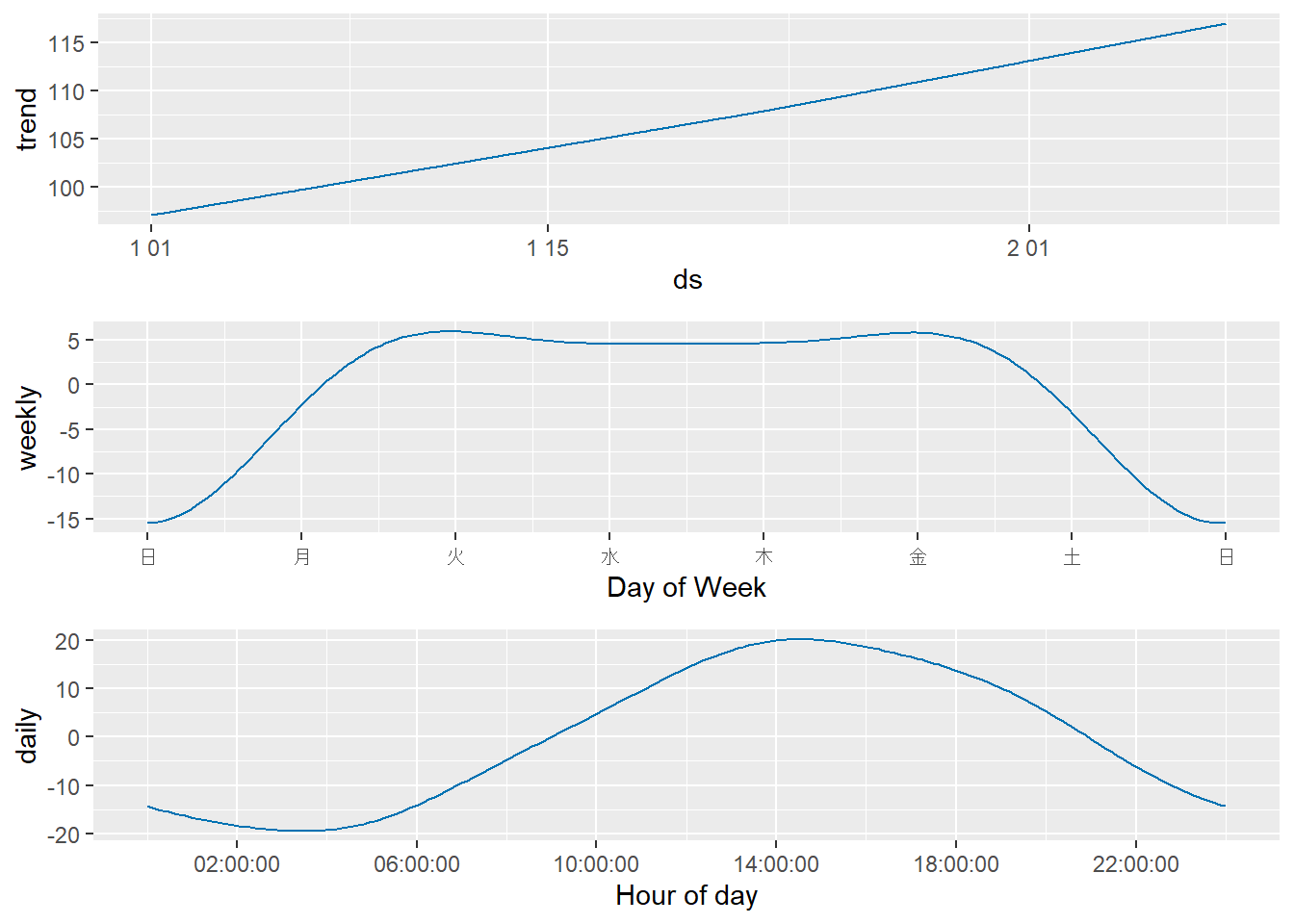
# 6. 成分のプロット
prophet_plot_components(m5_daily, forecast5_daily)作成した時間単位データの一部を確認:
ds y
1 2023-01-01 00:00:00 66.51044
2 2023-01-01 01:00:00 67.62580
3 2023-01-01 02:00:00 68.82009
4 2023-01-01 03:00:00 63.92541
5 2023-01-01 04:00:00 54.58592
6 2023-01-01 05:00:00 59.39318daily のプロットが追加され、1日の中での周期性がほぼ設定通りにモデル化されていることがわかります。
以上です。