Rで 線形代数:シルベスター行列 を確認します。
シルベスター行列とは
シルベスター行列(Sylvester Matrix)とは、2つの1変数多項式から作られる正方行列のことです。この行列の最も重要な役割は、2つの多項式が共通の根(解)を持つかどうかを判定することです。
定義
2つの多項式 p(x) と q(x) があるとします。
-
p(x) = a_m * x^m + a_{m-1} * x^{m-1} + ... + a_1 * x + a_0(m次式) -
q(x) = b_n * x^n + b_{n-1} * x^{n-1} + ... + b_1 * x + b_0(n次式)
このとき、p(x) と q(x) のシルベスター行列 S(p, q) は、サイズが (m + n) × (m + n) の正方行列となり、以下のように構成されます。
- 最初の
n行には、多項式p(x)の係数(a_m, a_{m-1}, ..., a_0)を1列ずつずらしながら配置します。 - 続く
m行には、多項式q(x)の係数(b_n, b_{n-1}, ..., b_0)を1列ずつずらしながら配置します。 - 行列の残りの要素はすべて
0で埋められます。
例: p(x) = a_2*x^2 + a_1*x + a_0 (m=2) と q(x) = b_1*x + b_0 (n=1) の場合、シルベスター行列は 3×3 行列になります。
| a2 a1 a0 |
| b1 b0 0 |
| 0 b1 b0 |上の行が p(x) の係数から、下の2行が q(x) の係数から作られています。
終結式(リザルタント)と共通根
シルベスター行列の行列式 det(S(p, q)) のことを終結式(Resultant)と呼びます。この終結式には、次の性質があります。
2つの多項式
p(x)とq(x)が共通の根を持つ ⇔ 終結式det(S(p, q))が 0 になる
この性質により、私たちは多項式の根を具体的に計算することなく、係数だけで作られる行列の行列式を調べるだけで、共通根の有無を判定できます。
R言語によるシミュレーション
以下に、シルベスター行列を生成し、その行列式(終結式)を計算することで、2つの多項式の共通根の有無を判定するシミュレーションのRコードを示します。
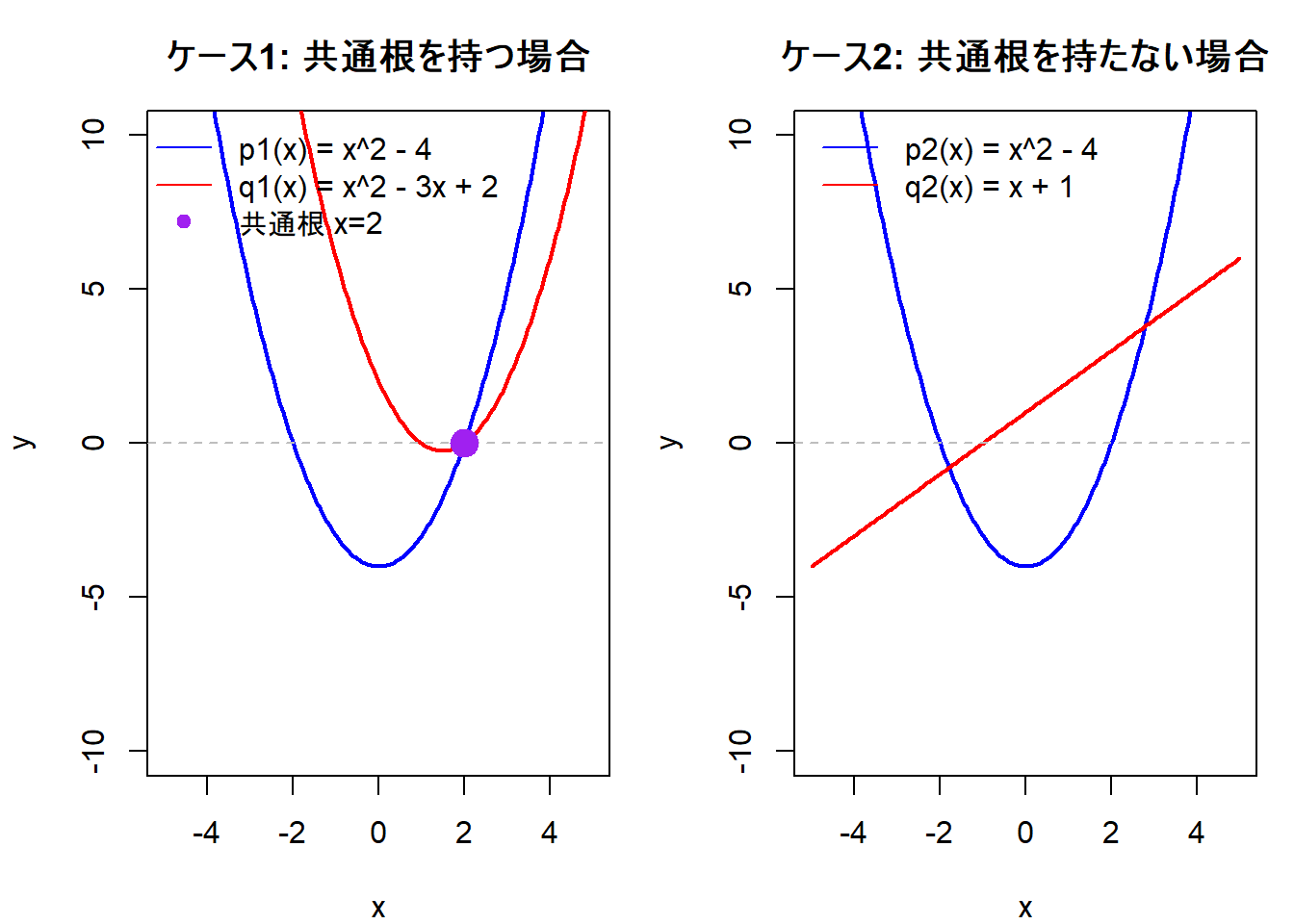
- ケース1: 共通根を持つ2つの多項式
- ケース2: 共通根を持たない2つの多項式
それぞれのケースでシルベスター行列とその行列式がどのようになるかを確認します。さらに、多項式のグラフをプロットして、結果を視覚的に検証します。
# 多項式の係数ベクトルからシルベスター行列を生成する関数
create_sylvester_matrix <- function(p_coeffs, q_coeffs) {
# 多項式の次数を取得 (係数の数 - 1)
m <- length(p_coeffs) - 1
n <- length(q_coeffs) - 1
# シルベスター行列のサイズは (m + n) x (m + n)
dim <- m + n
# 0で初期化された行列を作成
sylvester_mat <- matrix(0, nrow = dim, ncol = dim)
# p(x)の係数を行列の上半分に配置
for (i in 1:n) {
sylvester_mat[i, i:(i + m)] <- p_coeffs
}
# q(x)の係数を下半分に配置
for (i in 1:m) {
sylvester_mat[n + i, i:(i + n)] <- q_coeffs
}
return(sylvester_mat)
}
# 多項式を計算するためのヘルパー関数
poly_eval <- function(x, coeffs) {
# 係数ベクトルの長さ
n <- length(coeffs)
# 高次の項から計算
sapply(x, function(val) {
sum(coeffs * val^((n - 1):0))
})
}
# --- シミュレーション開始 ---
cat("====================================================\n")
cat(" シルベスター行列のシミュレーション\n")
cat("====================================================\n\n")
# ケース1: 共通根を持つ多項式
cat("--- ケース1: 共通根を持つ多項式 ---\n\n")
# p1(x) = x^2 - 4 = (x - 2)(x + 2)
# 根は x = 2, -2
p1_coeffs <- c(1, 0, -4)
# q1(x) = x^2 - 3x + 2 = (x - 1)(x - 2)
# 根は x = 1, 2
q1_coeffs <- c(1, -3, 2)
cat("多項式 p1(x) = x^2 - 4\n")
cat("多項式 q1(x) = x^2 - 3x + 2\n")
cat("これらの多項式は共通根 x = 2 を持ちます。\n\n")
# シルベスター行列を生成
S1 <- create_sylvester_matrix(p1_coeffs, q1_coeffs)
cat("生成されたシルベスター行列 S1:\n")
print(S1)
# 行列式(終結式)を計算
det_S1 <- det(S1)
cat("\n行列式 (終結式) det(S1) =", det_S1, "\n")
cat("-> 結果: 行列式が0になりました。理論通り、共通根を持つことが確認できました。\n\n")
# ケース2: 共通根を持たない多項式
cat("\n--- ケース2: 共通根を持たない多項式 ---\n\n")
# p2(x) = x^2 - 4 = (x - 2)(x + 2)
# 根は x = 2, -2
p2_coeffs <- c(1, 0, -4)
# q2(x) = x + 1
# 根は x = -1
q2_coeffs <- c(1, 1)
cat("多項式 p2(x) = x^2 - 4\n")
cat("多項式 q2(x) = x + 1\n")
cat("これらの多項式は共通根を持ちません。\n\n")
# シルベスター行列を生成
S2 <- create_sylvester_matrix(p2_coeffs, q2_coeffs)
cat("生成されたシルベスター行列 S2:\n")
print(S2)
# 行列式(終結式)を計算
det_S2 <- det(S2)
cat("\n行列式 (終結式) det(S2) =", det_S2, "\n")
cat("-> 結果: 行列式が0ではありません。理論通り、共通根を持たないことが確認できました。\n")
# --- 結果の可視化 ---
# 描画範囲を設定
x_range <- seq(-5, 5, length.out = 200)
# 描画デバイスを2分割
par(mfrow = c(1, 2), mar = c(4, 4, 3, 1))
# ケース1のプロット
plot(x_range, poly_eval(x_range, p1_coeffs),
type = "l", col = "blue", lwd = 2,
ylim = c(-10, 10), xlab = "x", ylab = "y",
main = "ケース1: 共通根を持つ場合"
)
lines(x_range, poly_eval(x_range, q1_coeffs), col = "red", lwd = 2)
abline(h = 0, lty = 2, col = "gray") # x軸
points(2, 0, col = "purple", pch = 19, cex = 2) # 共通根
legend("topleft",
legend = c("p1(x) = x^2 - 4", "q1(x) = x^2 - 3x + 2", "共通根 x=2"),
col = c("blue", "red", "purple"), lty = c(1, 1, NA), pch = c(NA, NA, 19), bty = "n"
)
# ケース2のプロット
plot(x_range, poly_eval(x_range, p2_coeffs),
type = "l", col = "blue", lwd = 2,
ylim = c(-10, 10), xlab = "x", ylab = "y",
main = "ケース2: 共通根を持たない場合"
)
lines(x_range, poly_eval(x_range, q2_coeffs), col = "red", lwd = 2)
abline(h = 0, lty = 2, col = "gray") # x軸
legend("topleft",
legend = c("p2(x) = x^2 - 4", "q2(x) = x + 1"),
col = c("blue", "red"), lty = 1, bty = "n"
)====================================================
シルベスター行列のシミュレーション
====================================================
--- ケース1: 共通根を持つ多項式 ---
多項式 p1(x) = x^2 - 4
多項式 q1(x) = x^2 - 3x + 2
これらの多項式は共通根 x = 2 を持ちます。
生成されたシルベスター行列 S1:
[,1] [,2] [,3] [,4]
[1,] 1 0 -4 0
[2,] 0 1 0 -4
[3,] 1 -3 2 0
[4,] 0 1 -3 2
行列式 (終結式) det(S1) = 0
-> 結果: 行列式が0になりました。理論通り、共通根を持つことが確認できました。
--- ケース2: 共通根を持たない多項式 ---
多項式 p2(x) = x^2 - 4
多項式 q2(x) = x + 1
これらの多項式は共通根を持ちません。
生成されたシルベスター行列 S2:
[,1] [,2] [,3]
[1,] 1 0 -4
[2,] 1 1 0
[3,] 0 1 1
行列式 (終結式) det(S2) = -3
-> 結果: 行列式が0ではありません。理論通り、共通根を持たないことが確認できました。以上です。