Rのパッケージから dlm を確認します。
1. dlmパッケージとは
dlmは、Rで動的線形モデル(Dynamic Linear Models, DLM)を扱うためのパッケージです。動的線形モデルは状態空間モデルの一種であり、時系列データの背後にある、直接観測できない「状態」(例えば、トレンドや季節性など)が時間と共にどの様に変化するかをモデル化します。
dlm パッケージにより、以下の分析が可能です。
- フィルタリング:新しいデータが得られるたびに、現在の状態を逐次的に推定します。
- 平滑化:すべてのデータを用いて、過去の状態をより正確に推定し直します。これにより、時系列データからノイズを除去し、トレンドや季節性といった成分を抽出できます。
- 予測:モデルに基づいて、将来の値を確率的に予測します。
2. サンプルデータの作成と可視化
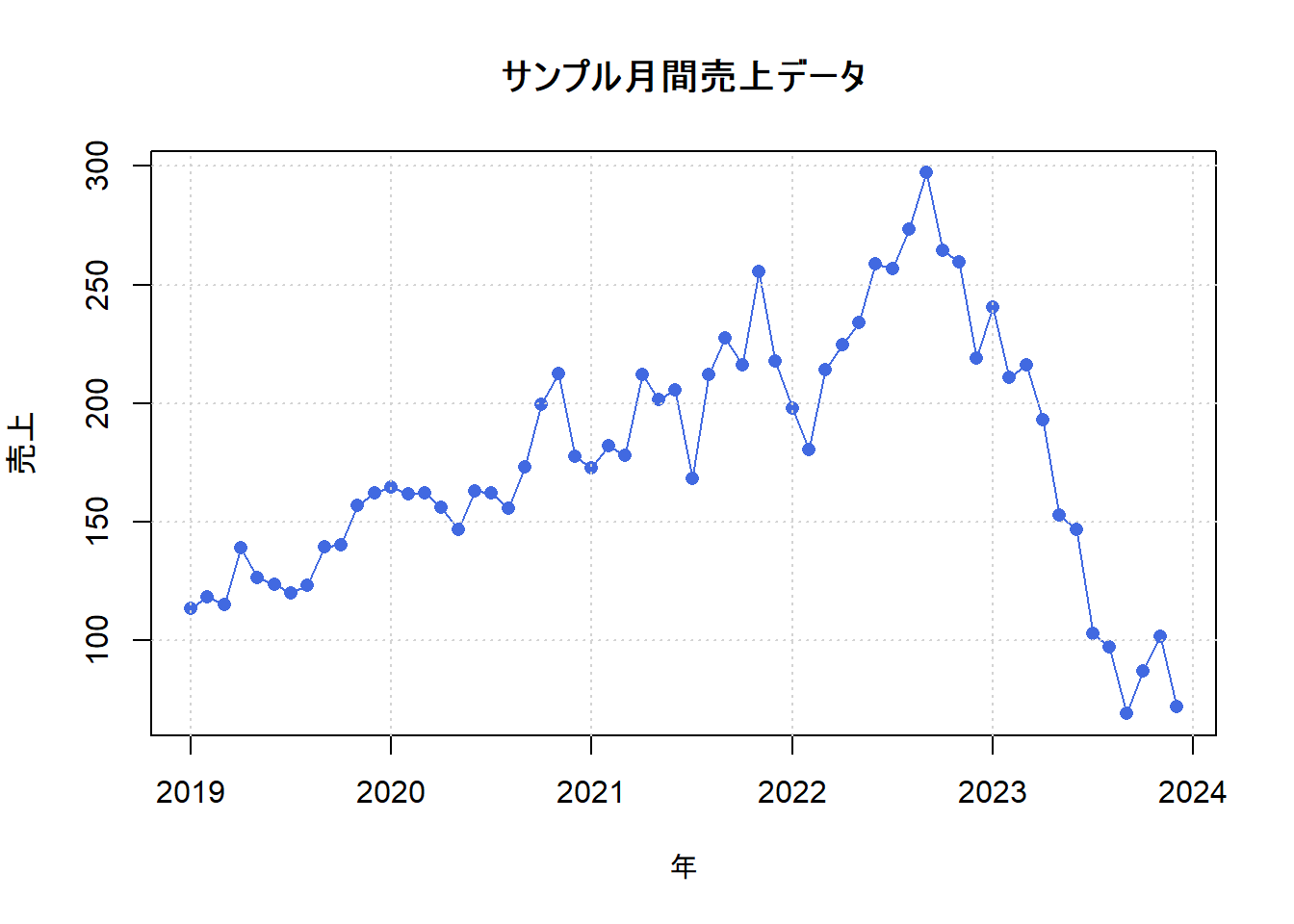
始めに、サンプルとする時系列データを作成します。ここでは、あるオンラインストアの月間売上データを想定します。データには、以下の要素が含まれていると仮定します。
- レベル(水準):売上の基本的な高さ。時間と共に変動します。
- トレンド(傾き):売上の成長率。同じく時間と共に変動します。
- 季節性:12か月周期のパターン。
- 観測ノイズ:上記以外のランダムな変動。
以上の要素を組み合わせて、60か月(5年分)のサンプルデータを生成します。
# dlmパッケージをロードします
library(dlm)
# 結果の再現性を確保するために乱数シードを設定します
seed <- 20250929
set.seed(seed)
# --- サンプルデータの生成 ---
# 期間を設定します (5年 = 60か月)
n <- 60
# 1. レベル成分 (ランダムウォーク)
# 基本的な売上水準が時間とともにランダムに変動する様子を表現します
level <- cumsum(rnorm(n, mean = 0, sd = 1.5)) + 100
# 2. トレンド成分 (ランダムウォーク)
# 売上の伸び率が時間とともにランダムに変動する様子を表現します
trend <- cumsum(rnorm(n, mean = 0, sd = 0.5)) + 2
# 3. 季節成分 (12か月周期)
# 毎年繰り返される売上のパターンを定義します
seasonal_effect <- c(5, 8, 10, 15, 12, 11, 9, 10, 18, 25, 35, 15)
seasonal <- rep(seasonal_effect, length.out = n)
# 4. 観測ノイズ
# 上記以外のランダムな変動です
noise <- rnorm(n, mean = 0, sd = 8)
# 全ての成分を足し合わせて、観測データを作成します
# (レベル) + (トレンド) * (時間) + (季節性) + (ノイズ)
observed_values <- level + trend * (1:n) + seasonal + noise
# tsオブジェクト(時系列オブジェクト)に変換します
# 2019年1月から始まる月次データとします
sales_ts <- ts(observed_values, start = c(2019, 1), frequency = 12)
# --- データの可視化 ---
plot(sales_ts,
type = "o",
pch = 16,
col = "royalblue",
main = "サンプル月間売上データ",
xlab = "年",
ylab = "売上",
lwd = 1
)
grid()3. 動的線形モデルの構築とパラメータ推定
次に、生成したデータに適合する動的線形モデルを構築します。データ生成の仮定に基づき、以下の3つの要素を組み合わせたモデルを考えます。
- ローカル線形トレンドモデル:レベルとトレンドの両方が時間と共に変動することを許容するモデルです。
dlmModPoly(order = 2)で定義します。 - 季節モデル:12か月周期の季節性を表現するモデルです。
dlmModSeas(frequency = 12)で定義します。 - ノイズ:観測ノイズと、各状態が変動する際のシステムノイズ(状態遷移ノイズ)です。これらのノイズの大きさ(分散)は未知ですので、データから推定する必要があります。
パラメータの推定には最尤法を用い、dlmMLE関数を使用します。
1. dlmModPoly関数
dlmModPoly関数は、dlmパッケージにおいて多項式トレンドモデルを作成するためのヘルパー関数です。
多項式トレンドモデルは、時系列のレベル(水準)やトレンド(傾き)、加速度といった、時間と共に変化する構造をモデル化する際に使用されます。
状態空間モデルは以下の2つの方程式で表現されます。
- 観測方程式: \(y_t = \boldsymbol{F}_t \boldsymbol{\theta}_t + v_t, \quad v_t \sim N(0, V_t)\)
- 観測値 \(y_t\) が、観測できない状態 \(\boldsymbol{\theta}_t\) からどのように生成されるかを記述します。
- 状態方程式: \(\boldsymbol{\theta}_t = \boldsymbol{G}_t \boldsymbol{\theta}_{t-1} + \boldsymbol{w}_t, \quad \boldsymbol{w}_t \sim N(0, W_t)\)
- 状態 \(\boldsymbol{\theta}_t\) が、一つ前の時点の状態 \(\boldsymbol{\theta}_{t-1}\) からどのように時間変化するかを記述します。
dlmModPoly関数の引数は、これらの数式で使われる行列やベクトルの要素(\(\boldsymbol{G}\), \(\boldsymbol{F}\), \(V\), \(W\))や、初期状態の分布(\(\boldsymbol{m}_0\), \(\boldsymbol{C}_0\))を設定するために使用されます。
以下に、各引数を確認します。
args(dlmModPoly)function (order = 2, dV = 1, dW = c(rep(0, order - 1), 1), m0 = rep(0,
order), C0 = 1e+07 * diag(nrow = order))
NULLorder
- モデルの次数を指定する整数です。これは状態ベクトル \(\boldsymbol{\theta}_t\) の次元数を決定し、モデルの複雑さを定義します。
-
order = 1: ランダムウォークモデル(またはローカルレベルモデル)を意味します。- 状態はレベル(水準)\(\mu_t\) のみです。
- 状態方程式: \(\mu_t = \mu_{t-1} + w_t\)
- 時系列の基本的な水準が時間とともにランダムに変動する様子をモデル化します。
-
order = 2: ローカル線形トレンドモデルを意味します。- 状態はレベル \(\mu_t\) とトレンド(傾き)\(\delta_t\) の2つです。
- 状態方程式:
- \(\mu_t = \mu_{t-1} + \delta_{t-1} + w_{\mu, t}\) (レベルは前回のレベル+前回のトレンド分だけ変化)
- \(\delta_t = \delta_{t-1} + w_{\delta, t}\) (トレンド自体もランダムに変化)
- 時系列のレベルと、その変化率であるトレンドの両方が時間とともに変動する、より柔軟なモデルです。
-
order = 3: レベル、トレンドに加え、トレンドの変化率(加速度)までを状態に含むモデルになります。 - デフォルト値:
2
dV
- 観測ノイズの分散 \(V_t\) を指定する数値です。
- 観測方程式 \(y_t = \boldsymbol{F}_t \boldsymbol{\theta}_t + v_t\) における、ノイズ項 \(v_t\) の分散を意味します。
- これは、モデルで説明しきれないランダムな変動の大きさを表します。この値が大きいほど、観測値はモデルが示す基本的な動き(レベルやトレンド)から大きくばらつきます。
- この引数で設定された値は、作成される
dlmオブジェクトのVコンポーネントに格納されます。 - 実際には観測ノイズの分散は未知であることがほとんどですので、
dlmMLE関数その他によりデータから最尤推定する必要があります。その場合、このdVの初期値は推定の出発点として使われますが、最終的には推定された値で上書きされます。
- デフォルト値:
1
dW
- システムノイズ(状態遷移ノイズ)の分散を指定するベクトルです。
- 状態方程式 \(\boldsymbol{\theta}_t = \boldsymbol{G}_t \boldsymbol{\theta}_{t-1} + \boldsymbol{w}_t\) における、ノイズ項 \(\boldsymbol{w}_t\) の共分散行列 \(W_t\) の対角成分を設定します。
-
dWはorderと同じ長さのベクトルで指定します。dW[i]は、状態ベクトルのi番目の要素が時間変化する際のランダムな変動の大きさを表します。 - 例えば
order = 2の場合、dW = c(dW_level, dW_trend)となり、dW_levelがレベルのシステムノイズ分散、dW_trendがトレンドのシステムノイズ分散に対応します。
- デフォルト値:
c(rep(0, order - 1), 1)-
order = 1の場合:dW = 1。レベルのシステムノイズ分散が1であることを意味します。 -
order = 2の場合:dW = c(0, 1)。これは、レベルのシステムノイズ分散が0、トレンドのシステムノイズ分散が1であることを意味します。レベルの変動は完全にトレンド \(\delta_{t-1}\) によって決まり、レベル自体にはランダムな変動が加わらない(\(w_{\mu, t}=0\))という、やや強い仮定を置いています。
-
m0
- 初期状態ベクトルの事前分布の平均 \(\boldsymbol{m}_0 = E[\boldsymbol{\theta}_0]\) を指定するベクトルです。
- これは、分析を開始する時点(\(t=0\))での各状態(レベルやトレンド)の期待値を意味します。
-
orderと同じ長さのベクトルで指定します。 - 例えば、時系列データの最初の値が100あたりであれば、レベルの初期値として
m0 = c(100, 0)のように設定することも考えられます(レベルの初期値100、トレンドの初期値0)。 - この引数で設定された値は、作成される
dlmオブジェクトのm0コンポーネントに格納されます。
- デフォルト値:
rep(0, order)- すべての状態の初期値の期待値が0であることを意味します。後述の
C0を大きく設定することで、この初期値の影響はデータによって更新されます。
- すべての状態の初期値の期待値が0であることを意味します。後述の
C0
- 初期状態ベクトルの事前分布の共分散行列 \(\boldsymbol{C}_0 = \text{Var}(\boldsymbol{\theta}_0)\) を指定する行列です。
- これは、分析を開始する時点(\(t=0\))での各状態の不確実性の大きさを表します。
-
order行order列の正方行列で指定します。 - この引数で設定された値は、作成される
dlmオブジェクトのC0コンポーネントに格納されます。
- デフォルト値:
1e+07 * diag(nrow = order)- これは、対角成分が非常に大きな値(\(10^7\))で、非対角成分が0の対角行列です。
- 対角成分(分散)が非常に大きいということは、初期状態に関する事前知識がほとんどなく、不確実性が非常に高いことを意味します(散漫事前分布)。
- このように設定することで、カルマンフィルタは初期状態の事前情報にほとんど依存せず、観測データに基づいて状態を推定するようになります。
2. dlmModSeas関数
dlmModSeas関数は、dlmパッケージにおいて季節性コンポーネントを表現するモデルを作成するためのヘルパー関数です。月次データや四半期データなど、周期的なパターンを持つ時系列データを分析する際に使用されます。
このモデルは、周期内のすべての季節効果の合計がゼロになる、という制約に基づいています。例えば、12ヶ月周期のモデルでは、1月-12月の季節効果をすべて足し合わせると0になります。この制約があるため、frequency - 1個の季節効果が決まれば、残りの1つは自動的に定まります。よって、内部的に扱われる状態ベクトルの次元数はfrequency - 1となります。
dlmModSeas関数の引数は、この季節性コンポーネントを定義する状態空間モデルの各要素を設定するために使用されます。
args(dlmModSeas)function (frequency, dV = 1, dW = c(1, rep(0, frequency - 2)),
m0 = rep(0, frequency - 1), C0 = 1e+07 * diag(nrow = frequency -
1))
NULLfrequency
- 季節性の周期を指定する整数です。この関数において唯一、指定が必須の引数です。
- 具体例:
- 月次データの場合:
frequency = 12 - 四半期データの場合:
frequency = 4 - 週次データ(曜日効果)の場合:
frequency = 7
- 月次データの場合:
- 状態ベクトルの次元数(
frequency - 1)や、状態遷移行列\(\boldsymbol{G}\)の形が本引数の値に基づいて自動的に設定されます。
dV
- 観測ノイズの分散 \(V_t\) を指定する数値です。
- これは、モデルが観測値\(y_t\)を説明する際に生じる誤差(\(y_t = \text{季節効果}_t + v_t\) における \(v_t\))の分散を意味します。
-
dlmModSeasは通常、dlmModPoly(トレンドモデル)など他のモデルと足し合わせて使用されます。dlmでは、複数のモデルを+で結合した場合、観測ノイズの分散Vは、原則として最初に指定されたモデルの値が使われるか、結合後のモデル全体に対して明示的に設定されます。 - よって、
dlmModSeasでdVを指定しても、最終的なモデルではその値が使われないことがあります。この引数は主に、季節モデルを単独で使用する場合や、モデルの仕様を形式的に整えるために設けられていると考えられます。 - デフォルト値:
1
dW
- システムノイズの分散を指定するベクトルです。これは、季節パターン自体が時間と共にどれだけ変化するかを制御する引数です。
- 状態方程式 \(\boldsymbol{\theta}_t = \boldsymbol{G}_t \boldsymbol{\theta}_{t-1} + \boldsymbol{w}_t\) における、ノイズ項\(\boldsymbol{w}_t\)の共分散行列\(W_t\)の対角成分を設定します。ベクトルの長さは
frequency - 1である必要があります。
- 状態方程式 \(\boldsymbol{\theta}_t = \boldsymbol{G}_t \boldsymbol{\theta}_{t-1} + \boldsymbol{w}_t\) における、ノイズ項\(\boldsymbol{w}_t\)の共分散行列\(W_t\)の対角成分を設定します。ベクトルの長さは
- 設定による挙動の違い:
- 動的季節モデル (Dynamic Seasonal Model):
dWにゼロでない値を設定すると、季節パターンが時間と共に変化することを許容します。- デフォルト値
c(1, rep(0, frequency - 2)): この設定では、システムノイズの最初の要素にのみ分散を与え、残りはゼロにしています。これにより、季節パターン全体が滑らかに変化していくようなモデルになります。例えば、ある年の「12月の売上のピーク」が、翌年には少し大きくなったり小さくなったりするような変動を捉えることができます。
- デフォルト値
- 静的季節モデル (Static / Fixed Seasonal Model):
dWをすべてゼロに設定した場合(例:dW = rep(0, frequency - 1))、季節パターンは時間を通じて変化しないと仮定されます。- この設定は、データ全体で一つの共通した季節パターンが存在すると仮定するものです。最初に推定された季節パターンが、将来にわたって全く同じ形で繰り返されることになります。
- 動的季節モデル (Dynamic Seasonal Model):
- パラメータ推定:
dWの値を事前に決めるのが難しい場合、dlmMLEを用いてデータから推定することが可能です。
m0
- 初期状態ベクトルの事前分布の平均 \(\boldsymbol{m}_0\) を指定するベクトルです。
- 分析を開始する時点(\(t=0\))での、
frequency - 1個の季節効果の期待値を意味します。 - この引数で設定された値は、作成される
dlmオブジェクトのm0コンポーネントに格納されます。
- 分析を開始する時点(\(t=0\))での、
- デフォルト値:
rep(0, frequency - 1)- 初期の季節効果の期待値はすべて0であると仮定します。後述の
C0を大きく設定することで、この初期値の影響はデータによってすぐに更新されます。
- 初期の季節効果の期待値はすべて0であると仮定します。後述の
C0
- 初期状態ベクトルの事前分布の共分散行列 \(\boldsymbol{C}_0\) を指定する行列です。
- 分析を開始する時点(\(t=0\))での季節効果の不確実性の大きさを表します。
-
frequency - 1行frequency - 1列の正方行列で指定します。
- デフォルト値:
1e+07 * diag(nrow = frequency - 1)- 対角成分が非常に大きな値(\(10^7\))である対角行列です。これは、初期の季節パターンについては何も情報がない(不確実性が非常に高い)ということを意味します(散漫事前分布)。
- このように設定することで、カルマンフィルタは初期状態の事前情報にほとんど依存せず、観測データに基づいて季節パターンを学習します。
3. dlmMLE関数
dlmMLE関数は、動的線形モデル(DLM)に含まれる未知のパラメータを、観測データに基づいて最尤法(Maximum Likelihood Estimation, MLE)を用いて推定する役割を担います。
最尤法とは、「観測されたデータが、そのモデルから生成される確率(尤度)が最も高くなるように、モデルのパラメータを決定する」推定手法です。dlmMLEは、尤度を最大化するパラメータ値を探索します。
推定対象となる代表的なパラメータは、観測ノイズやシステムノイズの分散です。これらのノイズの大きさが事前に分からない場合、この関数を使ってデータから客観的に推定する必要があります。
以下に、各引数の詳細を確認します。
args(dlmMLE)function (y, parm, build, method = "L-BFGS-B", ..., debug = FALSE)
NULLy
- 分析対象の時系列データを指定します。
dlmMLEはこのデータyの尤度を最大化するパラメータを探します。 - データ形式:
-
tsオブジェクト: Rで時系列データを扱う標準的な形式です。開始時点や周期といった情報が含まれているため、最も扱いやすい形式です。 - 数値ベクトル (
vector): 単変量の時系列データの場合に利用できます。 - 行列 (
matrix): 各列が異なる変数を表す、多変量の時系列データの場合に利用します。行が時間の進行に対応します。
-
- この引数は必ず指定する必要があります。
parm
- 推定したいパラメータの初期値を数値ベクトルで指定します。
-
dlmMLEは内部で数値最適化アルゴリズム(デフォルトではoptim関数)を用いて、最適なパラメータを探します。parmは、その探索を開始する出発点となります。適切な初期値を与えることで、アルゴリズムがより速く、またより良い解(尤度が最も高い点)に収束する可能性が高まります。 - DLMで推定するパラメータが分散である場合、分散は常に正の値を取る必要がありますが、最適化アルゴリズムはパラメータ空間を制約なしに探索しようとすることがあります。
- この問題を回避するための一つのテクニックとして、対数スケールで最適化を行います。つまり、
build関数の中でexp(par)のようにパラメータを指数変換して分散として用いるのです。こうすることで、par自体が負の値を取っても、exp(par)は常に正となり、分散の制約を満たします。 - このテクニックを用いる場合、
parmには分散の対数を取った値を初期値として設定します。例えば、分散の初期値を1としたい場合はlog(1) = 0ですので、parm = 0と設定します。
build
-
dlmモデルを構築するための関数を指定します。このbuild関数は、dlmMLEが最適化の各ステップで呼び出す、ユーザー定義の「設計図」のようなものです。 - 関数の仕様:
- 引数:
parmで指定したのと同じ長さのパラメータベクトルを、唯一の引数として受け取る必要があります。 - 返り値:
dlmオブジェクトを返す必要があります。
- 引数:
- 内部的な動作:
dlmMLEは以下の処理を繰り返します。- 最適化アルゴリズムが、新しいパラメータの候補値
pを生成します。 -
dlmMLEは、ユーザーが定義したbuild関数をbuild(p)のように呼び出します。 -
build関数は、パラメータpを使ってdlmオブジェクト(例えば、VやdWにexp(p)を設定したモデル)を構築し、返します。 -
dlmMLEは、その返されたdlmオブジェクトとデータyを使って尤度を計算します。 - 最適化アルゴリズムは、計算された尤度を基に、さらに尤度が高くなりそうな次のパラメータ候補値を探索します。
- 最適化アルゴリズムが、新しいパラメータの候補値
- この引数により、ユーザーは
build関数を自由に記述することで、カスタムモデルのパラメータ推定も可能になります。
method
- 尤度を最大化するために内部で使用する、数値最適化アルゴリズムを指定します。
-
dlmMLEは、Rの標準的な汎用最適化関数であるstats::optimを利用しています。よって、method引数にはoptimで利用可能なアルゴリズム名を文字列で指定します。 - デフォルト値:
"L-BFGS-B"- これは、ボックス制約付き準ニュートン法です。パラメータの取りうる値に上限や下限(ボックス制約)を設定できる特徴があります。
- その他の選択肢:
"Nelder-Mead","BFGS","CG","SANN"など、optimがサポートする他の手法も指定できます。
...
- 説明:
optim関数に渡す、その他の追加引数を指定するために使用します。 - 最適化プロセスの挙動を細かく制御するための
controlリストを渡すことが出来ます。 - 具体例:
-
control = list(maxit = 1000): 最大反復回数をデフォルトの100回から1000回に増やす。 -
control = list(trace = 1): 最適化の過程(反復ごとのパラメータ値や目的関数値)を表示する。 -
control = list(reltol = 1e-12): 収束判定の相対的な許容誤差をより厳しくする。
# 使用例 dlmMLE(y, parm, build, control = list(trace = 1, maxit = 1000)) -
debug
- デバッグ情報を出力するかどうかを指定する論理値(
TRUEまたはFALSE)です。 -
debug = TRUEの場合:-
dlmMLEがbuild関数を呼び出すたびに、その際に渡されたパラメータベクトルと、計算された負の対数尤度(optimは最小化を行うため)の値を画面に出力します。 - これは、
control = list(trace = ...)よりも詳細な情報を提供します。
-
- 利用シーン:
-
build関数が特定のパラメータ値でエラーを返す場合、どの値で問題が起きているのかを特定するのに役立ちます。 - 最適化が予期せぬ挙動を示す場合に、内部で何が起きているかを調査する手がかりとなります。
-
- デフォルト値:
FALSE(デバッグ情報は表示されません)。
# --- モデル構築関数の定義 ---
# パラメータ(ノイズの分散)を引数として、dlmオブジェクトを返す関数を定義します
# これにより、最尤法で最適なパラメータを探すことができます
build_sales_model <- function(par) {
# ローカル線形トレンドモデル (レベル + トレンド)
trend_model <- dlmModPoly(order = 2, dV = 0, dW = exp(par[1:2]))
# 12か月周期の季節モデル
# 季節性の変動はないと仮定し、dWは0に固定します
seasonal_model <- dlmModSeas(frequency = 12, dV = 0, dW = rep(0, 11))
# モデルを結合します
model <- trend_model + seasonal_model
# 観測ノイズの分散を設定します
model$V <- exp(par[3])
return(model)
}
# --- パラメータの最尤推定 ---
# dlmMLEを用いて、モデルのパラメータを推定します
# parmにはパラメータの初期値を設定します
# buildには上で定義したモデル構築関数を指定します
mle_fit <- dlmMLE(
y = sales_ts,
parm = c(log(1), log(1), log(10)),
build = build_sales_model
)
# 収束の確認 (0なら成功)
cat("最尤推定の収束コード:", mle_fit$convergence, "(0は成功を示します)\n")
# 推定されたパラメータを使って、最終的なモデルを構築します
sales_model_est <- build_sales_model(mle_fit$par)
# --- 推定された分散パラメータの確認 ---
# dlmでは分散が負にならないように対数スケールで最適化を行うため、exp()で元に戻します
estimated_variances <- exp(mle_fit$par)
cat("\n推定された分散パラメータ:\n")
cat("レベルのシステムノイズ分散 (W[1,1]):", estimated_variances[1], "\n")
cat("トレンドのシステムノイズ分散 (W[2,2]):", estimated_variances[2], "\n")
cat("観測ノイズ分散 (V):", estimated_variances[3], "\n")最尤推定の収束コード: 0 (0は成功を示します)
推定された分散パラメータ:
レベルのシステムノイズ分散 (W[1,1]): 284.6552
トレンドのシステムノイズ分散 (W[2,2]): 3.30265
観測ノイズ分散 (V): 17.69443 最尤推定によって、データに最もフィットするノイズの分散が計算されました。これらの値が設定されたモデルを用いて、次のステップに進みます。
4. 平滑化による成分分解
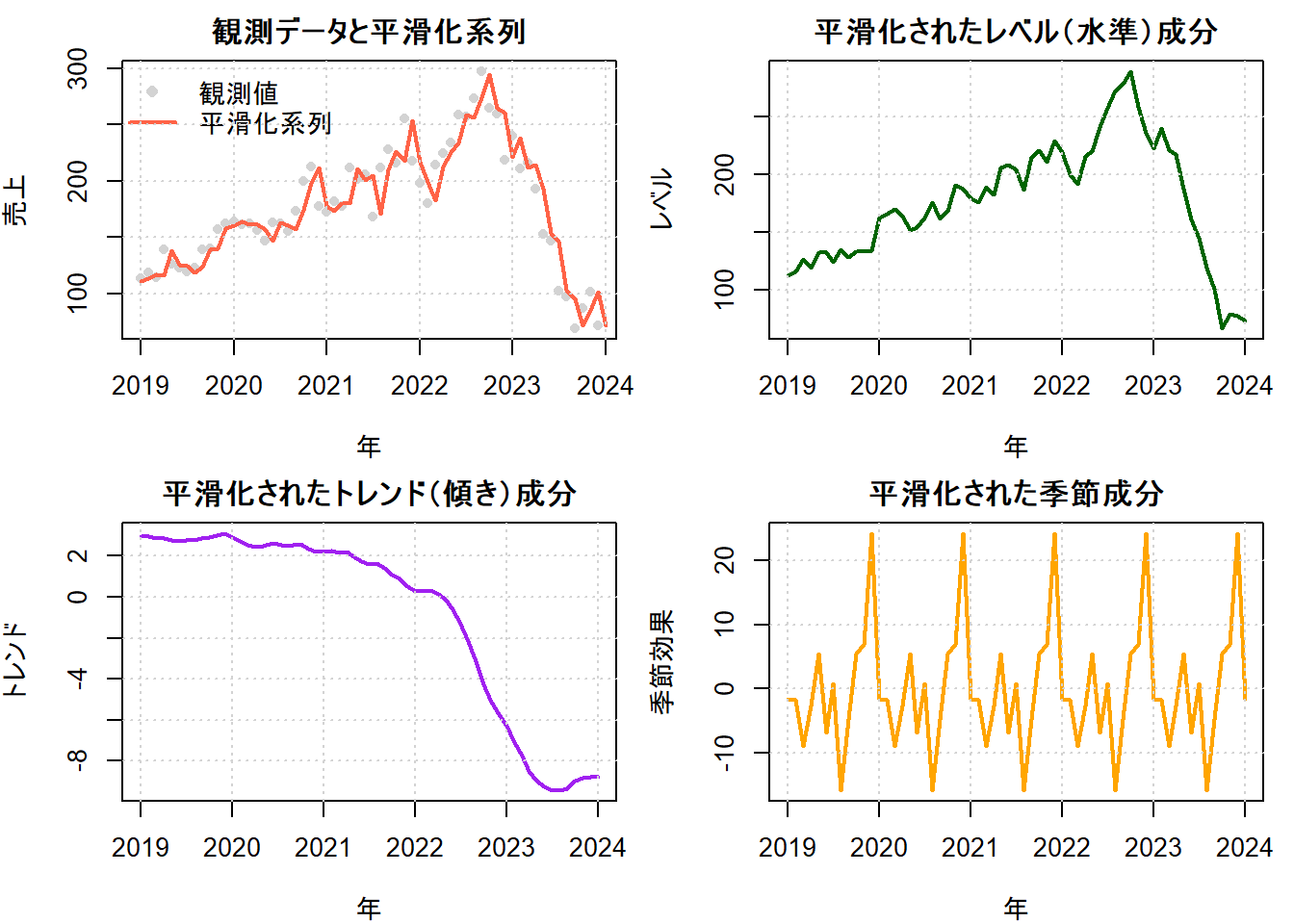
平滑化とは、期間中のすべてのデータを用いて、各時点における状態(レベル、トレンド、季節性)を再推定する処理です。これにより、ノイズが除去された滑らかな時系列成分を抽出できます。これはdlmSmooth関数で実行します。
平滑化によって得られた各成分を可視化することで、売上データがどのように分解されるかを確認してみましょう。
# --- 平滑化の実行 ---
# dlmSmooth関数にデータと推定済みモデルを渡します
smoothed_result <- dlmSmooth(sales_ts, sales_model_est)
# --- 平滑化された状態の抽出 ---
# smoothed_result$s には、各時点の平滑化された状態ベクトルが格納されています
# 1列目: レベル, 2列目: トレンド, 3列目以降: 季節性
smooth_level <- smoothed_result$s[, 1]
smooth_trend <- smoothed_result$s[, 2]
smooth_seasonal <- smoothed_result$s[, 3]
# 平滑化されたレベルと季節性をtsオブジェクトに変換します
smooth_level_ts <- ts(smooth_level, start = c(2019, 1), frequency = 12)
smooth_trend_ts <- ts(smooth_trend, start = c(2019, 1), frequency = 12)
smooth_seasonal_ts <- ts(smooth_seasonal, start = c(2019, 1), frequency = 12)
# 平滑化された観測値(レベル+トレンド+季節性)を計算します
smooth_observed_ts <- smooth_level_ts + smooth_seasonal_ts
# --- 結果のプロット ---
# 描画エリアを4分割します
par(mfrow = c(2, 2), mar = c(4, 4, 2, 1))
# 1. 観測データと平滑化系列の比較
plot(sales_ts,
type = "p", pch = 16, col = "lightgrey",
main = "観測データと平滑化系列",
xlab = "年", ylab = "売上"
)
lines(smooth_observed_ts, col = "tomato", lwd = 2)
legend("topleft",
legend = c("観測値", "平滑化系列"),
col = c("lightgrey", "tomato"),
lty = c(NA, 1), pch = c(16, NA),
lwd = c(NA, 2), bty = "n"
)
grid()
# 2. 抽出されたレベル成分
plot(smooth_level_ts,
main = "平滑化されたレベル(水準)成分",
xlab = "年", ylab = "レベル",
col = "darkgreen", lwd = 2
)
grid()
# 3. 抽出されたトレンド成分
plot(smooth_trend_ts,
main = "平滑化されたトレンド(傾き)成分",
xlab = "年", ylab = "トレンド",
col = "purple", lwd = 2
)
grid()
# 4. 抽出された季節成分
plot(smooth_seasonal_ts,
main = "平滑化された季節成分",
xlab = "年", ylab = "季節効果",
col = "orange", lwd = 2
)
grid()5. 将来予測
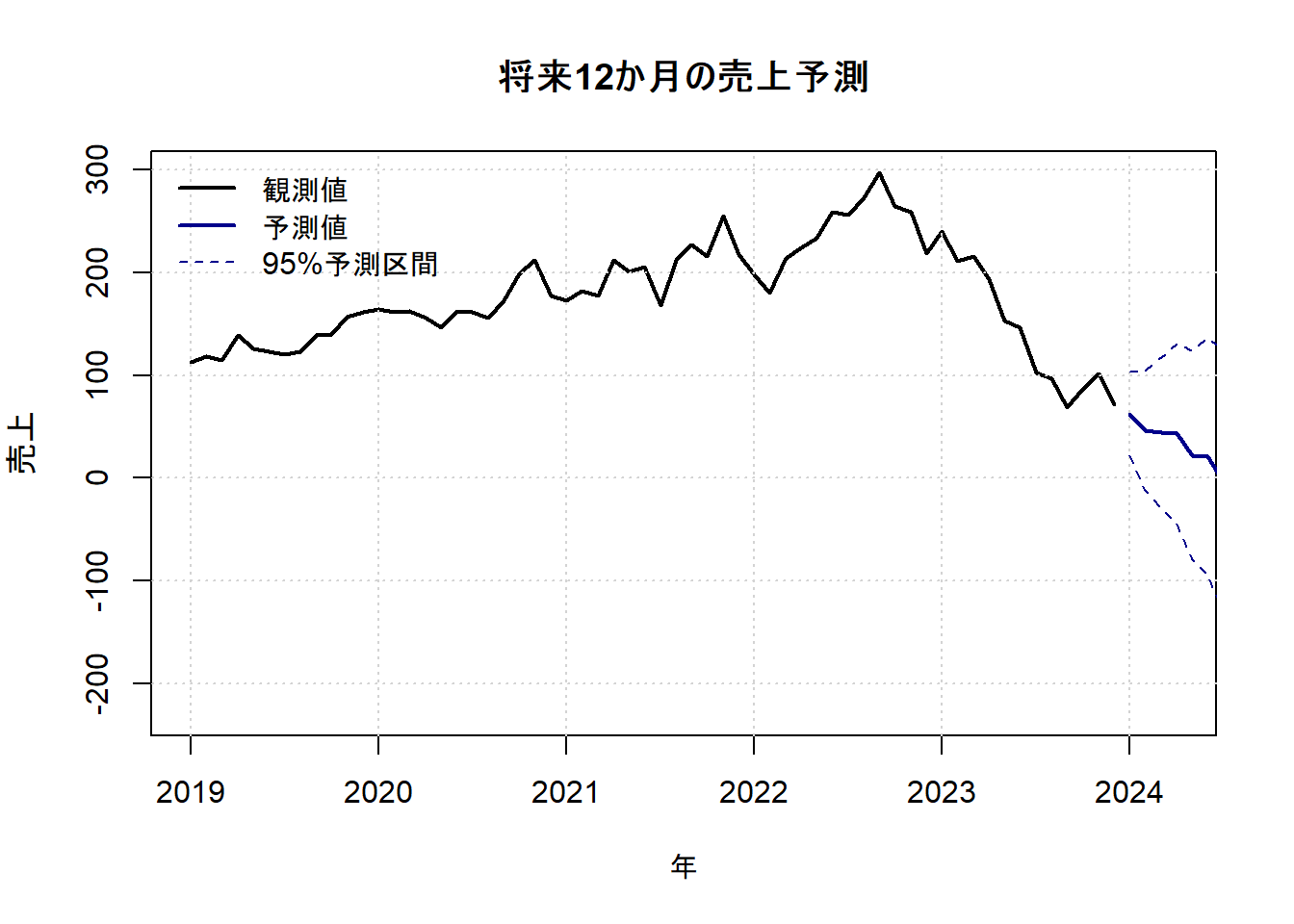
最後に、構築したモデルを使って将来の売上を予測します。dlmForecast関数は、最後の観測時点の状態から将来をシミュレーションします。ここでは12か月先までを予測し、予測区間(将来の値が95%の確率で入ると期待される範囲)も同時に描画します。
# --- フィルタリングの実行 ---
# 予測はフィルタリング結果(最後の時点の状態)を利用して行います
filtered_result <- dlmFilter(sales_ts, sales_model_est)
# --- 予測の実行 ---
# nAheadで予測期間を指定します(12か月先)
n_ahead <- 12
forecasted_result <- dlmForecast(filtered_result, nAhead = n_ahead)
# --- 予測結果の抽出 ---
# f: 予測値の時系列
# Q: 予測値の分散のリスト
forecast_values <- forecasted_result$f
forecast_variances <- unlist(forecasted_result$Q)
# 予測区間の計算 (95%区間)
confidence_level <- 0.95
z_score <- qnorm(1 - (1 - confidence_level) / 2)
ci_upper <- forecast_values + z_score * sqrt(forecast_variances)
ci_lower <- forecast_values - z_score * sqrt(forecast_variances)
# --- 予測結果のプロット ---
# y軸の範囲を調整して、予測区間が収まるようにします
y_limit <- range(sales_ts, ci_lower, ci_upper)
x_limit <- c(start(sales_ts)[1], end(forecast_values)[1] + 0.25)
plot(sales_ts,
xlim = x_limit,
ylim = y_limit,
main = "将来12か月の売上予測",
xlab = "年",
ylab = "売上",
lwd = 2
)
grid()
# 予測値をプロット
lines(forecast_values, col = "darkblue", lwd = 2, lty = "solid")
# 95%予測区間をプロット
lines(ci_upper, col = "darkblue", lwd = 1, lty = "dashed")
lines(ci_lower, col = "darkblue", lwd = 1, lty = "dashed")
legend("topleft",
legend = c("観測値", "予測値", "95%予測区間"),
col = c("black", "darkblue", "darkblue"),
lty = c("solid", "solid", "dashed"),
lwd = c(2, 2, 1),
bty = "n"
)観測期間の終わりのトレンドと季節性を引き継いで、将来の値が予測されています。予測区間は、将来に進むほど不確実性が増大するため、幅が広がっていくことが分かります。
6. 関数 dlmMLE の引数 y に指定する時系列データは定常である必要はあるか
結論
dlmMLEに渡す時系列データは定常である必要はありません。
理由
dlmが非定常なデータを扱える理由は、そのモデルの構造そのものにあります。dlmが構築する動的線形モデル(状態空間モデル)は、観測される時系列データの背後にある、直接観測できない「状態」の時間的な変化をモデル化します。
非定常性を「状態」が吸収する 動的線形モデルは、以下の2つの方程式で構成されます。
- 観測方程式: \(y_t = \boldsymbol{F}_t \boldsymbol{\theta}_t + v_t\)
- 状態方程式: \(\boldsymbol{\theta}_t = \boldsymbol{G}_t \boldsymbol{\theta}_{t-1} + \boldsymbol{w}_t\)
ここで、観測データ\(y_t\)の非定常性(例:平均が時間と共に変化するトレンド)は、状態ベクトル\(\boldsymbol{\theta}_t\)が吸収します。例えば、\(\boldsymbol{\theta}_t\)にレベル(水準)やトレンド(傾き)といった要素を含めることで、それらが時間と共に変化する様子を状態方程式で直接的に表現します。
モデルが仮定するのは、観測ノイズ\(v_t\)やシステムノイズ\(\boldsymbol{w}_t\)が(通常は)定常であるということであり、観測データ\(y_t\)や状態\(\boldsymbol{\theta}_t\)そのものが定常であることは仮定しません。
カルマンフィルタが逐次的に状態を更新する
dlmMLEが内部で尤度を計算するために用いるカルマンフィルタは、逐次的なアルゴリズムです。過去のデータから現在の状態を予測し、新しい観測データが得られたらその予測を修正(更新)するという処理を繰り返します。このメカニズムは、状態が非定常であっても問題なく機能します。状態の平均や分散が時間と共に変化していくことを前提として計算が進みますので、データ全体が定常である必要はないのです。
対比:ARIMAモデルとの比較
ARIMAモデル: ARIMAモデルの
AR(自己回帰)部分とMA(移動平均)部分は、定常な時系列データを前提とします。ですので、データにトレンドなどの非定常性がある場合、まず階差(Differencing)を取ることでデータを定常化させる必要があります。この階差の操作がARIMAモデルのI(和分)に相当します。つまり、ARIMAモデルは「データを定常化してからモデルを適用する」というアプローチを取ります。動的線形モデル (dlm):
dlmは全く異なるアプローチを取ります。階差によってトレンドを除去するのではなく、「トレンドそのもの」を状態の一部としてモデルに組み込みます。これにより、トレンドが時間と共にどう変化していくかを直接的に推定・分析することができます。データを加工して定常化させる必要がないのは、モデル自身が非定常性を表現する能力を持っているからです。
具体例:ローカル線形トレンドモデルの場合
上記サンプルで用いたローカル線形トレンドモデル(dlmModPoly(order = 2))の状態方程式は以下のようになっています。
- レベル(水準): \(\mu_t = \mu_{t-1} + \delta_{t-1} + w_{\mu, t}\)
- トレンド(傾き): \(\delta_t = \delta_{t-1} + w_{\delta, t}\)
2つの式を確認しますと、レベル\(\mu_t\)の期待値は、前の時点のレベル\(\mu_{t-1}\)にトレンド\(\delta_{t-1}\)を加えたものになります。これは、時系列の平均が時間と共に変化していくことを直接的に表現しており、まさに非定常性の定義そのものです。dlmはこのような非定常な構造をモデル化するために設計されているのです。
以上です。