Rの関数から dlmFilter {dlm} を確認します。
本ポストはこちらの続きです。

dlmFilter関数の引数
dlmFilter関数は、dlmパッケージにおいてフィルタリング(Filtering)を実行するための関数です。
フィルタリングとは、時系列データを時点t=1から順番に処理していき、各時点tまでの観測データを用いて、その時点tにおける状態(レベル、トレンドなど)を推定する逐次的な処理です。この処理はカルマンフィルタアルゴリズムそのものです。
この処理は、新しい情報(観測値)が得られるたびに、それまでの状態の予測を修正・更新していくプロセスと考えることができます。例えば、気象予報で、新しい観測データが入るたびに明日の天気予報を更新していく作業に似ています。
フィルタリングによって得られた結果は、現在の状態をリアルタイムで監視したり、将来予測(dlmForecast)の出発点として用いたり、あるいは平滑化(dlmSmooth)の前処理として利用されたりします。
以下に、関数の引数を確認します。
library(dlm)
args(dlmFilter)function (y, mod, debug = FALSE, simplify = FALSE)
NULLy
- 分析対象の時系列データを指定します。
dlmFilterは、このデータyを使って、モデルmodで定義された状態を逐次的に推定していきます。 - データ形式:
-
tsオブジェクト(推奨) - 数値ベクトル (
vector) - 行列 (
matrix) (多変量時系列データの場合)
-
- この引数は必ず指定する必要があります。
mod
- フィルタリング計算に使用する動的線形モデルを、
dlmクラスのオブジェクトとして指定します。 -
modオブジェクトは、モデルの構造(FF,GGなど)だけでなく、ノイズの分散・共分散(V,W)や初期状態(m0,C0)といった全てのパラメータが、具体的な数値として設定済みである必要があります。 - 通常、
dlmMLE関数を用いてデータから最尤推定したパラメータを使い、最終的なモデルを構築した上で、そのモデルオブジェクトをこのmod引数に渡します。 - この引数は必ず指定する必要があります。
debug
- デバッグ情報を出力するかどうかを指定する論理値(
TRUEまたはFALSE)です。 -
debug = TRUEの場合: フィルタリングの各時間ステップ(t=1, 2, ...)において、状態ベクトルやその共分散行列などの中間計算結果が出力されます。これは、カルマンフィルタの「予測ステップ」と「更新ステップ」で計算される値に対応します。 - デフォルト値:
FALSE。
simplify
- 関数の返り値の形式を単純化するかどうかを指定する論理値(
TRUEまたはFALSE)です。 -
simplify = FALSE(デフォルト):-
dlmFilteredというクラスのリストを返します。このオブジェクトには、フィルタリングされた状態系列だけでなく、その共分散行列、1期先予測値、対数尤度などの情報が格納されています。 - この
dlmFilteredオブジェクトは、後続のdlmSmooth関数やdlmForecast関数にそのまま渡すことができるように設計されています。
-
-
simplify = TRUE:- フィルタリングされた状態ベクトル\(\boldsymbol{m}_t\)の時系列のみを行列として返します。行列の各行が時点、各列が状態に対応します。
- 平滑化や予測を行わず、単純にフィルタリングされた状態の値だけが必要な場合に、結果をシンプルに取り出したいときに利用されます。
返り値 (dlmFilteredオブジェクト) とカルマンフィルタの動作
simplify = FALSEの場合、dlmFilterはdlmFilteredオブジェクトを返します。
-
a: 1期先予測状態ベクトル (\(a_t = E[\theta_t | y_{1:t-1}]\)) の時系列。- 「更新前」の状態。時点
t-1までの情報で予測された、時点tの状態の期待値です。
- 「更新前」の状態。時点
-
m: フィルタリング状態ベクトル (\(m_t = E[\theta_t | y_{1:t}]\)) の時系列。- 「更新後」の状態。時点
tの観測値\(y_t\)を取り込んでaを修正した、その時点tの状態の期待値です。
- 「更新後」の状態。時点
-
f: 1期先予測観測値 (\(f_t = E[y_t | y_{1:t-1}]\)) の時系列。aから計算される、時点tの観測値の予測です。 -
logLik: 対数尤度。モデルが観測データをどの程度に説明できているかを示す指標です。
カルマンフィルタの本質は、各時点tにおいて、
- 予測:
m_{t-1}からa_tを計算する。 - 更新:
a_tと観測値y_tの差(予測誤差)を利用して、a_tを修正しm_tを計算する。
というプロセスを繰り返すことにあります。
この「更新」の効果を、コード例を通じて視覚的に確認してみましょう。
コードによる具体例:フィルタリングによる状態の更新
ここでは、dlmFilterを実行し、各時点tにおける「更新前の予測状態 (a_t)」と「更新後のフィルタリング状態 (m_t)」を比較します。この比較により、観測データによって状態推定がどのように修正されるか(引き寄せられるか)を確認します。
# サンプルデータとモデルの準備
seed <- 20250930
set.seed(seed)
y_sample <- ts(cumsum(rnorm(50, sd = 2)) + rnorm(50, sd = 5), start = 2020)
# 今回はローカルレベルモデル(order=1)を使用します
build_func <- function(par) {
dlmModPoly(order = 1, dV = exp(par[1]), dW = exp(par[2]))
}
mle_fit <- dlmMLE(y_sample, parm = c(0, 0), build = build_func)
final_model <- build_func(mle_fit$par)
# --- dlmFilterの実行 ---
filtered_result <- dlmFilter(y = y_sample, mod = final_model)
# --- 結果の抽出(状態が1つでも複数でも動作するコード) ---
# 観測期間の長さを取得
T_len <- length(y_sample)
# 1期先予測状態 a_t (更新前) を t=1,...,T で抽出
a_matrix <- as.matrix(filtered_result$a)
pred_state <- ts(a_matrix[1:T_len, 1], start = start(y_sample), frequency = frequency(y_sample))
# フィルタリング状態 m_t (更新後) を t=1,...,T で抽出
m_matrix <- as.matrix(filtered_result$m)
# filtered_result$m には t=0 の初期状態が含まれるため、2番目から T+1 番目までを抽出
filtered_state <- ts(m_matrix[2:(T_len + 1), 1], start = start(y_sample), frequency = frequency(y_sample))
# --- 結果の数値確認 (最初の6時点) ---
cat("--- フィルタリング結果の一部の数値比較 ---\n")
print(head(cbind(
観測値 = y_sample,
更新前の予測 = pred_state,
更新後の推定 = filtered_state
)))
# --- 結果のプロット ---
plot(y_sample,
type = "p", pch = 16, cex = 1.2, col = "grey",
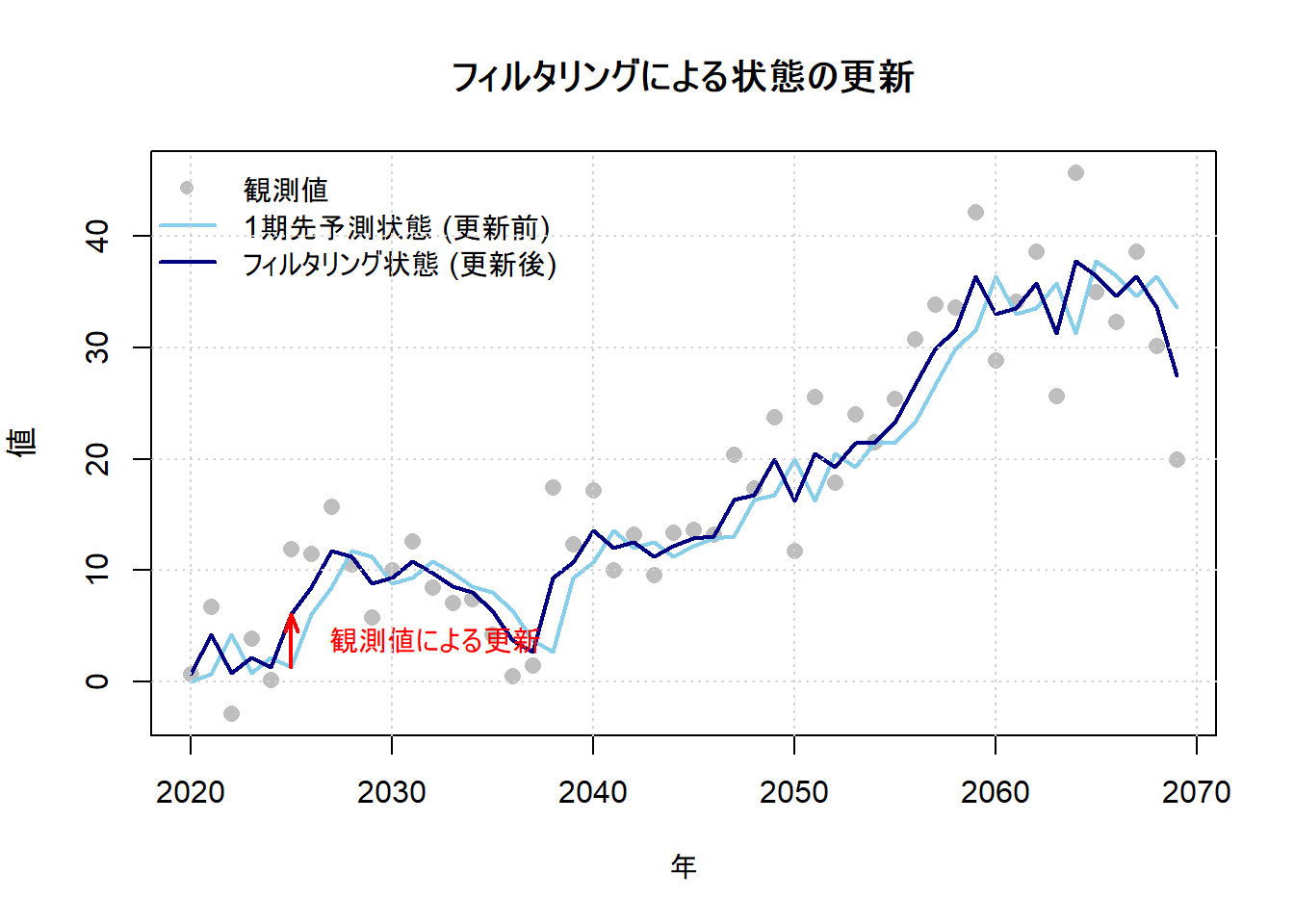
main = "フィルタリングによる状態の更新",
xlab = "年", ylab = "値"
)
lines(pred_state, col = "skyblue", lwd = 2, lty = "solid")
lines(filtered_state, col = "navy", lwd = 2, lty = "solid")
# 違いを分かりやすくするため、特定の点(6番目)に矢印を追加
arrows(
x0 = time(y_sample)[6], y0 = pred_state[6],
x1 = time(y_sample)[6], y1 = filtered_state[6],
length = 0.1, angle = 20, col = "red", lwd = 2
)
text(time(y_sample)[6] + 1,
(pred_state[6] + filtered_state[6]) / 2,
"観測値による更新",
col = "red", pos = 4
)
legend("topleft",
legend = c("観測値", "1期先予測状態 (更新前)", "フィルタリング状態 (更新後)"),
col = c("grey", "skyblue", "navy"),
lty = c(NA, 1, 1),
pch = c(16, NA, NA),
lwd = c(NA, 2, 2),
bty = "n"
)
grid()--- フィルタリング結果の一部の数値比較 ---
Time Series:
Start = 2020
End = 2025
Frequency = 1
観測値 更新前の予測 更新後の推定
2020 0.6721799 0.0000000 0.6721785
2021 6.7481707 0.6721785 4.1827355
2022 -2.8868466 4.1827355 0.7456901
2023 3.8428431 0.7456901 2.1728424
2024 0.1628444 2.1728424 1.2616825
2025 11.9216544 1.2616825 6.0700635数値の比較: 表を見ると、各時点において「更新前の予測」と「更新後の推定」の値が異なっていることが分かります。例えば2021年では、
更新前の予測は0.672でしたが、観測値の6.748を考慮した結果、更新後の推定は4.183へと上方修正されています。Figure 1 の解釈:
- 水色の実線(更新前の予測,
a_t): 前の時点までの情報だけで予測された、状態の「事前」の推定値です。 - 灰色の点(観測値,
y_t): その時点で得られた新しい情報です。 - 紺色の実線(更新後の推定,
m_t): 新しい観測値(灰色の点)を考慮して、予測値(水色の実線)を修正した後の、状態の「事後」の推定値です。
Figure 1 上の赤い矢印が示すように、予測値(水色の線)は、その時点の観測値(灰色の点)の方向に更新され、フィルタリング後の推定値(紺色の線)になっています。これがカルマンフィルタによる逐次的な学習・更新プロセスです。
- 水色の実線(更新前の予測,
以上です。