Rの関数:ur.pp {urca}

Rの関数から ur.pp {urca} を確認します。

本ポストはこちらの続きです。

Rの関数:pp.test {tseries}
Rの関数から pp.test {tseries} を確認します。本ポストはこちらの続きです。pp.test関数についてpp.testは、フィリップス–ペロン検定（Phillips-Perron Test） を実行するための関数です。この検定...
www.saecanet.com
2025.10.11

ur.pp関数について

ur.pp関数は、tseriesパッケージのpp.testと同様に、フィリップス–ペロン（Phillips-Perron, PP）検定 を実行するための関数です。ADF検定と同じく、時系列データに単位根が存在するかどうかを検定する目的で使用されます。

PP検定は、誤差項の自己相関に対処するために、ADF検定のように回帰モデルにラグ項を追加するのではなく、検定統計量自体を非パラメトリックな手法で修正する点が特徴です。

tseries::pp.test関数と比較して、p値だけでなく、検定統計量と棄却限界値（Critical Value）の出力や、検定の前提となるモデルをmodel引数で指定てきる点などが特徴です。

検定の帰無仮説は一貫して「単位根が存在する（時系列は非定常である）」です。

ur.pp関数の引数について

library(urca)
args(ur.pp)
function (x, type = c("Z-alpha", "Z-tau"), model = c("constant", 
    "trend"), lags = c("short", "long"), use.lag = NULL) 
NULL

x

検定の対象となる時系列データを指定します。数値ベクトルなどが該当します。

type

計算および報告される検定統計量の種類を指定します。

  • "Z-alpha"（デフォルト）: 正規化された係数に基づく検定統計量（Zα統計量）です。
  • "Z-tau": 通常の回帰分析から得られるt統計量を、非パラメトリックな手法で『修正』した検定統計量（Zτ統計量）です。

model

検定の基礎となる回帰モデルの決定論的要素（deterministic components）を指定します。ur.df関数のtype引数に相当する引数です。

  • "constant"（デフォルト）:定数項（ドリフト）のみを含むモデルで検定します。データがゼロではない一定の平均の周りで変動している（もしくはドリフト付きランダムウォークである）ような場合に選択します。
  • "trend":定数項と時間トレンドの両方を含むモデルで検定します。データが時間と共に上昇または下降する傾向線に沿って変動しているような場合に選択します。

lags

検定統計量を非パラメトリックに修正する際に用いるラグの切り捨てパラメータの計算方法を指定します。

  • "short"（デフォルト）: trunc(4*(n/100)^0.25) という計算式でラグを決定します。
  • "long": trunc(12*(n/100)^0.25) という計算式でラグを決定します。

use.lag

ラグの切り捨てパラメータを整数で直接指定したい場合に使用します。この引数に値が設定されると、lags引数の設定は無視されます。

シミュレーション

ur.pp関数の挙動、特にmodel引数の役割を確認するために、それぞれのモデルに対応する2種類のサンプルデータを生成し、検定を実行します。

なお、有意水準は5%とします。

# 再現性を確保するために乱数のシードを設定します
seed <- 20251012
set.seed(seed)

# シミュレーションのためのサンプルデータ作成
# データポイントの数を定義します
n <- 200

# 1. model = "constant" に対応するデータ（ドリフト付きランダムウォーク）
# 単位根を持つ非定常データです
data_constant <- cumsum(rnorm(n) + 0.3)

# 2. model = "trend" に対応するデータ（トレンド定常過程）
# 時間トレンドの周りを定常的に変動する過程です。単位根は持ちません。
data_trend <- 5 + 0.5 * (1:n) + arima.sim(model = list(ar = 0.7), n = n, sd = 2)

# 描画デバイスを1行2列に分割します
par(mfrow = c(1, 2), mar = c(4, 4, 3, 2))

# プロット1
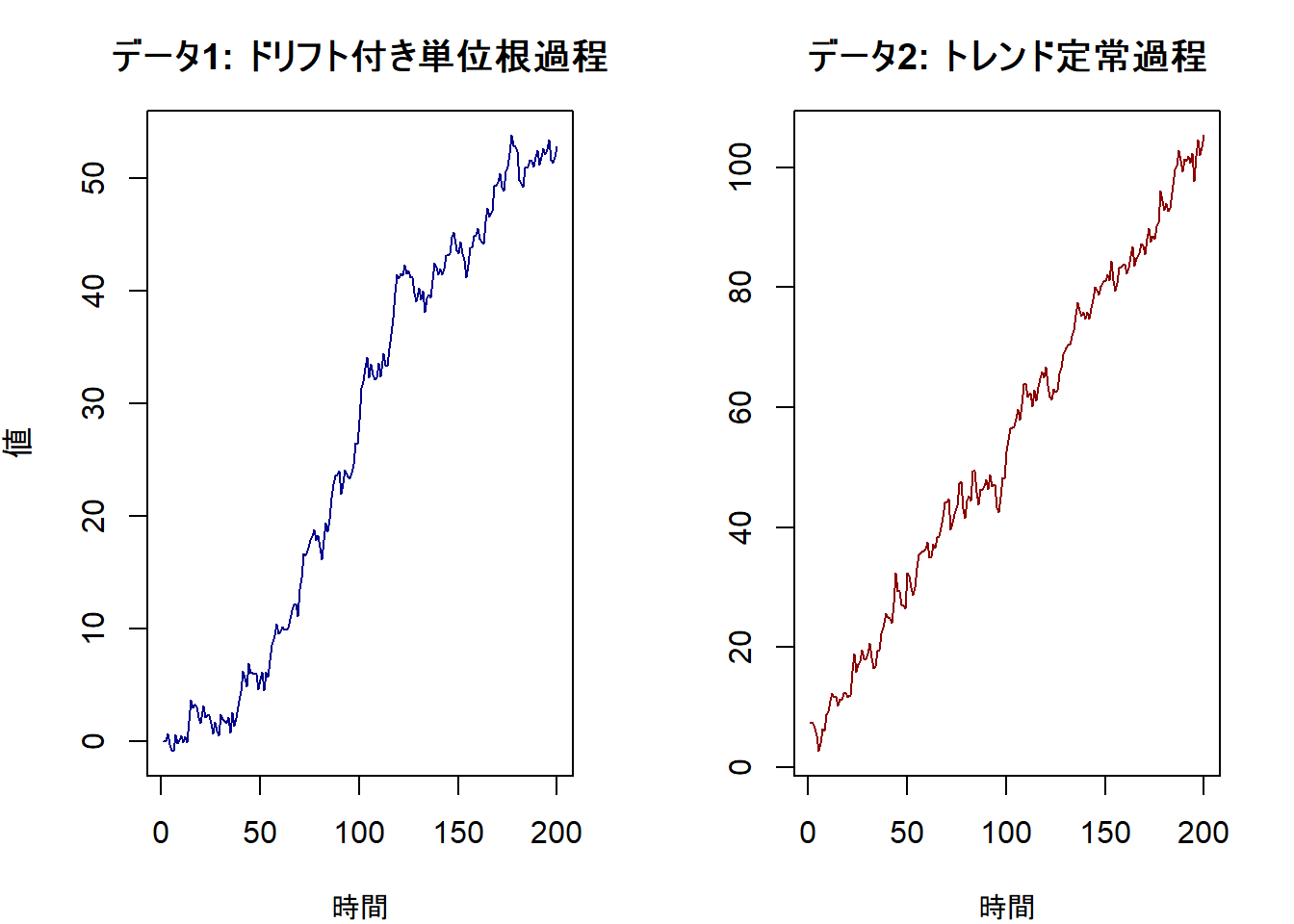
plot(data_constant,
  type = "l", col = "darkblue",
  main = "データ1: ドリフト付き単位根過程",
  xlab = "時間", ylab = "値"
)

# プロット2
plot(data_trend,
  type = "l", col = "darkred",
  main = "データ2: トレンド定常過程",
  xlab = "時間", ylab = ""
)
Figure 1
# ur.ppの実行と結果の解釈
cat("--- ケース1：ドリフト付き単位根データに model='constant' で検定 ---\n")
# このデータは単位根を持つため、帰無仮説は棄却されないと予測されます。
# type="Z-tau", model="constant" で実行します。
pp_result_const <- ur.pp(data_constant, type = "Z-tau", model = "constant")
summary(pp_result_const)
--- ケース1：ドリフト付き単位根データに model='constant' で検定 ---

################################## 
# Phillips-Perron Unit Root Test # 
################################## 

Test regression with intercept 


Call:
lm(formula = y ~ y.l1)

Residuals:
     Min       1Q   Median       3Q      Max 
-2.82798 -0.75956 -0.02545  0.77822  2.54733 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.308350   0.125633   2.454    0.015 *  
y.l1        0.998390   0.003871 257.884   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.027 on 197 degrees of freedom
Multiple R-squared:  0.997, Adjusted R-squared:  0.997 
F-statistic: 6.65e+04 on 1 and 197 DF,  p-value: < 2.2e-16


Value of test-statistic, type: Z-tau  is: -0.4106 

         aux. Z statistics
Z-tau-mu            2.4831

Critical values for Z statistics: 
                     1pct     5pct     10pct
critical values -3.464384 -2.87607 -2.574439

ur.pp検定結果の確認

この出力は、ドリフト付きの単位根過程として生成されたdata_constantに対して、model="constant"（定数項を含むモデル）を指定してフィリップス–ペロン検定を実行した結果です。

検定の基本情報
################################## 
# Phillips-Perron Unit Root Test # 
################################## 

Test regression with intercept
  • Phillips-Perron Unit Root Test: 実行された検定がフィリップス–ペロン単位根検定であることを示します。
  • Test regression with intercept: model="constant"が指定され、検定の内部で切片項（定数項）を含む回帰モデルが使用されたことを意味します。
内部で使用された回帰モデル
Call:
lm(formula = y ~ y.l1)

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.308350   0.125633   2.454    0.015 *  
y.l1        0.998390   0.003871 257.884   <2e-16 ***
  • Call:: PP検定の基礎となる、内部で実行された回帰モデルの数式です。現在の値yを1期前の値y.l1で回帰しています。
  • Coefficients:: 回帰分析の結果です。

    • y.l1の係数（Estimate）が0.998390 と 1 に近くなっており、これは単位根（係数が1）がデータに存在することを示す根拠です。
    • こちらに表示されているt valueやPr(>|t|)は、通常の線形回帰における統計量です。時系列データが単位根を持つ可能性がある場合、これらの値はt分布には従わないため、単位根の有無を判断するために直接使用することはできません。
診断情報
Multiple R-squared:  0.997, Adjusted R-squared:  0.997
  • Multiple R-squared:: 決定係数が0.997と高い値を示しています。非定常な時系列同士を回帰させると、実際には無関係でも見かけ上高い相関が示されることがあり、「見せかけの回帰」と呼ばれます。この現象も、データが非定常（単位根を持つ）であることを間接的に示唆しています。
検定の主結果と結論の導出

出力の最後の部分が、単位根の有無を判断するための箇所です。

Value of test-statistic, type: Z-tau  is: -0.4106 

Critical values for Z statistics: 
                     1pct     5pct     10pct
critical values -3.464384 -2.87607 -2.574439

  • Value of test-statistic, type: Z-tau is: -0.4106: こちらがフィリップス–ペロン検定の最終的な検定統計量（Zτ統計量）です。回帰分析から得られたt統計量を、誤差項の自己相関を考慮して非パラメトリックに修正した値です。

  • Critical values for Z statistics:: 検定の判断基準となる棄却限界値（Critical Value）です。

    • 1pct: 有意水準1%の棄却限界値 (-3.464)
    • 5pct: 有意水準5%の棄却限界値 (-2.876)
    • 10pct: 有意水準10%の棄却限界値 (-2.574)
結論の導出

検定の判断は、「検定統計量」と「棄却限界値」を比較して行います。

  • 帰無仮説 (H₀): 単位根が存在する（データは非定常である）。
  • 判断ルール: 検定統計量 < 棄却限界値 であれば、帰無仮説を棄却する。

設定した有意水準5%で判断します。

  • 検定統計量: -0.4106
  • 5%棄却限界値: -2.87607

-0.4106 > -2.87607ですので、検定統計量は棄却限界値を下回っていません。

ですので、帰無仮説「単位根が存在する」を棄却することはできません。

この検定結果は、y.l1の係数が1に近いという回帰分析の結果とも整合的であり、「この時系列データは非定常な単位根過程である」という結論を支持します。データ生成時の設定とも一致しており、検定が正しく機能していることが確認できます。

cat("--- ケース2：トレンド定常データに model='trend' で検定 ---\n")
# こちらのデータは単位根を持たないため、帰無仮説は棄却されると予測されます。
pp_result_trend <- ur.pp(data_trend, type = "Z-tau", model = "trend")
summary(pp_result_trend)
--- ケース2：トレンド定常データに model='trend' で検定 ---

################################## 
# Phillips-Perron Unit Root Test # 
################################## 

Test regression with intercept and trend 


Call:
lm(formula = y ~ y.l1 + trend)

Residuals:
    Min      1Q  Median      3Q     Max 
-5.5079 -1.2439  0.1021  1.2086  4.9541 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 15.73003    2.67695   5.876 1.78e-08 ***
y.l1         0.71809    0.04947  14.517  < 2e-16 ***
trend        0.14140    0.02481   5.699 4.36e-08 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.806 on 196 degrees of freedom
Multiple R-squared:  0.9961,    Adjusted R-squared:  0.9961 
F-statistic: 2.528e+04 on 2 and 196 DF,  p-value: < 2.2e-16


Value of test-statistic, type: Z-tau  is: -5.7171 

           aux. Z statistics
Z-tau-mu              5.8076
Z-tau-beta            5.7179

Critical values for Z statistics: 
                     1pct      5pct     10pct
critical values -4.006973 -3.433347 -3.140242

ur.pp検定結果の確認

この出力は、トレンド定常過程として生成されたdata_trendに対して、model="trend"（定数項と時間トレンド項の両方を含むモデル）を指定してフィリップス–ペロン検定を実行した結果です。

検定の基本情報
################################## 
# Phillips-Perron Unit Root Test # 
################################## 

Test regression with intercept and trend
  • Phillips-Perron Unit Root Test: 実行された検定がフィリップス–ペロン単位根検定であることを示します。
  • Test regression with intercept and trend: model="trend"が指定され、検定の内部で切片項（定数項）と時間トレンド項を含む回帰モデルが使用されたことを意味します。
内部で使用された回帰モデル
Call:
lm(formula = y ~ y.l1 + trend)

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 15.73003    2.67695   5.876 1.78e-08 ***
y.l1         0.71809    0.04947  14.517  < 2e-16 ***
trend        0.14140    0.02481   5.699 4.36e-08 ***
  • Call:: PP検定の基礎となる、内部で実行された回帰モデルの数式です。現在の値yを、1期前の値y.l1と時間トレンドtrendで回帰しています。
  • Coefficients:: 回帰分析の結果です。

    • y.l1の係数（Estimate）が0.71809 となっており、これは1よりも小さい値です。この事実は、時系列が過去の値の影響を減衰させて平均（この場合はトレンド線）に戻ろうとする性質、すなわち定常性を持つことを示唆しています。
    • trendの係数が正の値で、かつ統計的に有意です。これは、このデータに上昇トレンドが存在することを示しています。
    • こちらのPr(>|t|)（p値）も、単位根の検定には利用できません。
検定の主結果と結論の導出

出力の最後の部分が、単位根の有無を判断するための箇所です。

Value of test-statistic, type: Z-tau  is: -5.7171 

           aux. Z statistics
Z-tau-mu              5.8076
Z-tau-beta            5.7179

Critical values for Z statistics: 
                     1pct      5pct     10pct
critical values -4.006973 -3.433347 -3.140242

  • Value of test-statistic, type: Z-tau is: -5.7171: こちらがフィリップス–ペロン検定の最終的な検定統計量（Zτ統計量）です。回帰分析から得られたt統計量を、誤差項の自己相関を考慮して非パラメトリックに修正した値になります。

  • Critical values for Z statistics:: 検定の判断基準となる棄却限界値（Critical Value）です。

    • 1pct: 有意水準1%の棄却限界値 (-4.007)
    • 5pct: 有意水準5%の棄却限界値 (-3.433)
    • 10pct: 有意水準10%の棄却限界値 (-3.140)
結論の導出

検定の判断は、「検定統計量」と「棄却限界値」を比較して行います。

  • 帰無仮説 (H₀): 単位根が存在する（データは非定常である）。
  • 判断ルール: 検定統計量 < 棄却限界値 であれば、帰無仮説を棄却する。

設定した有意水準5%で判断します。

  • 検定統計量: -5.7171
  • 5%棄却限界値: -3.433347

-5.7171 < -3.433347ですので、検定統計量は棄却限界値を下回っています。

ですので、帰無仮説「単位根が存在する」は棄却されます。

総合的な結論

帰無仮説が棄却されたため、このデータは単位根を持たないと結論付けられます。さらに、回帰モデルにおいて時間トレンド項が統計的に有意でした。

これらの結果を総合すると、「この時系列データは確定的な時間トレンドの周りで変動する、トレンド定常過程である」と結論付けられます。データ生成時の設定とも一致しており、検定がデータの性質を捉えていることが確認できます。

以上です。