Rの関数:ur.kpss {urca}

Rの関数から ur.kpss {urca} を確認します。

本ポストはこちらの続きです。

Rの関数から kpss.test {tseries} を確認します。本ポストはこちらの続きです。kpss.test関数についてkpss.testは、クウィアトコウスキー–フィリップス–シュミット–シン（Kwiatkowski-Phillip...

ur.kpss関数について

ur.kpss関数は、tseriesパッケージのkpss.testと同様に、クウィアトコウスキー–フィリップス–シュミット–シン（Kwiatkowski-Phillips-Schmidt-Shin, KPSS）検定 を実行するための関数です。

この検定は、以下の通り、ADF検定やPP検定とは仮説が逆転しています。

帰無仮説 (H₀): 時系列は定常（またはトレンド定常）である。
対立仮説 (H₁): 時系列は単位根を持つ（非定常である）。

tseries::kpss.testがp値を直接出力するのに対し、urca::ur.kpssはur.dfやur.ppと同様に、検定統計量と棄却限界値（Critical Value）を併記して出力します。

ur.kpss関数の引数について

library(urca)
args(ur.kpss)

function (y, type = c("mu", "tau"), lags = c("short", "long", 
    "nil"), use.lag = NULL) 
NULL

`y`

検定の対象となる時系列データを指定します。

`type`

帰無仮説として仮定する定常性の種類を指定します。tseries::kpss.testのnull引数に相当します。

"mu" (μ) （デフォルト）: 帰無仮説をStationarity round a constant level(本ポストでは以降「水準定常性」と呼称)とします。データが一定の平均値（μ）の周りで変動している状態を「定常」と仮定します。tseries::kpss.testのnull = "Level"に対応します。
"tau" (τ): 帰無仮説をStationarity around a deterministic trend(本ポストでは以降「トレンド定常性」と呼称)とします。データが時間トレンド（τ）の周りで変動している状態を「定常」と仮定します。tseries::kpss.testのnull = "Trend"に対応します。

`lags`

検定統計量の計算に使用するラグの切り捨てパラメータの計算方法を指定します。

"short"（デフォルト）: 短い方のラグ計算式 trunc(4*(n/100)^0.25) を使用します。
"long": 長い方のラグ計算式 trunc(12*(n/100)^0.25) を使用します。
"nil": ラグを0に設定します。これは誤差項に自己相関がないと仮定する場合の検定に相当します。

`use.lag`

ラグの切り捨てパラメータを整数で直接指定したい場合に使用します。この引数に値が設定されると、lags引数の設定は無視されます。

シミュレーション

ur.kpss関数の挙動を確認するために、定常なデータと非定常なデータを作成し、それぞれに検定を適用して結果を比較します。

なお、有意水準は5%とします。

# 再現性を確保するために乱数のシードを設定します
seed <- 20251014
set.seed(seed)

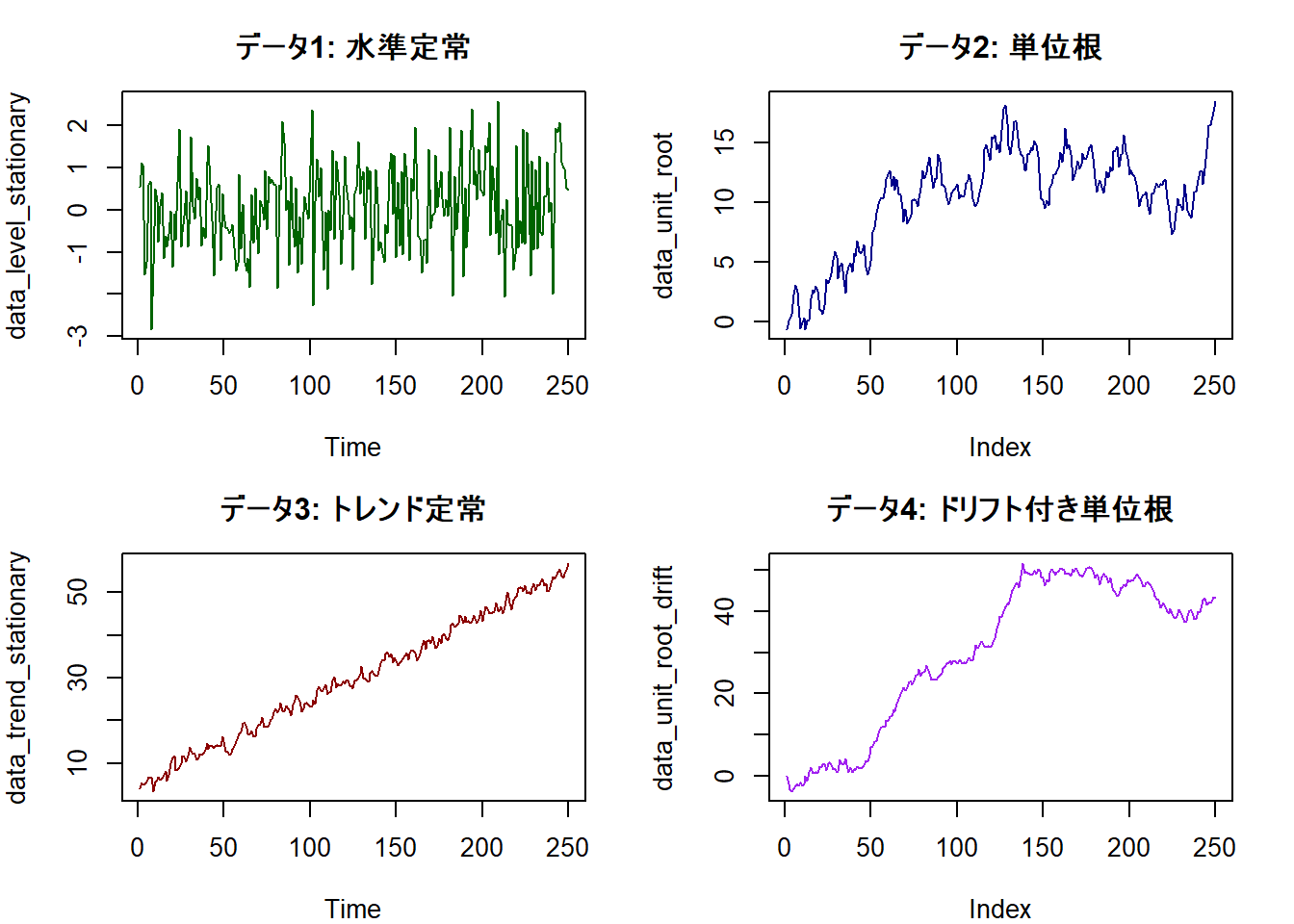
# シミュレーションのためのサンプルデータ作成

n <- 250

# 1. 水準定常なデータ (帰無仮説が真)
# type='mu'用データ：水準定常過程
data_level_stationary <- arima.sim(model = list(ar = 0.1), n = n)

# 2. 単位根を持つデータ (対立仮説が真)
# type='mu'用データ：単位根過程
data_unit_root <- cumsum(rnorm(n))

# 3. トレンド定常なデータ (帰無仮説が真)
# type='tau'用データ：トレンド定常過程
data_trend_stationary <- 5 + 0.2 * (1:n) + arima.sim(model = list(ar = 0.6), n = n)

# 4. ドリフト付き単位根データ (対立仮説が真)
# type='tau'用データ：ドリフト付き単位根過程
data_unit_root_drift <- cumsum(rnorm(n) + 0.2)


# 作成したデータの可視化
par(mfrow = c(2, 2), mar = c(4, 4, 3, 2))
plot(data_level_stationary, type = "l", main = "データ1: 水準定常", col = "darkgreen")
plot(data_unit_root, type = "l", main = "データ2: 単位根", col = "darkblue")
plot(data_trend_stationary, type = "l", main = "データ3: トレンド定常", col = "darkred")
plot(data_unit_root_drift, type = "l", main = "データ4: ドリフト付き単位根", col = "purple")

# --- ケース1: 水準定常データ ---
cat("--- ケース1：水準定常データに type='mu' で検定 ---\n")
# データは定常ですので、帰無仮説「水準定常である」は棄却されないと予測されます。
# つまり、検定統計量が棄却限界値を下回ると予測されます。
kpss_result1 <- ur.kpss(data_level_stationary, type = "mu")
summary(kpss_result1)

--- ケース1：水準定常データに type='mu' で検定 ---

####################### 
# KPSS Unit Root Test # 
####################### 

Test is of type: mu with 5 lags. 

Value of test-statistic is: 0.6817 

Critical value for a significance level of: 
                10pct  5pct 2.5pct  1pct
critical values 0.347 0.463  0.574 0.739

`ur.kpss`検定結果の確認

この出力は、水準定常な過程として生成された data_level_stationary に対して、type="mu"（水準定常性）を帰無仮説としてKPSS検定を実行した結果です。

####################### 
# KPSS Unit Root Test # 
####################### 

Test is of type: mu with 5 lags. 

Value of test-statistic is: 0.1691 

Critical value for a significance level of: 
                10pct  5pct 2.5pct  1pct
critical values 0.347 0.463  0.574 0.739

各項目の確認

KPSS Unit Root Test
実行された検定がKPSS単位根検定であることを示しています。
Test is of type: mu with 5 lags.
検定の前提条件を示しています。
- type: mu: 帰無仮説が水準定常性（データは一定の平均値μの周りで変動する）であることを意味します。
- with 5 lags: 検定統計量の計算に使用されたラグの切り捨てパラメータが5であることを示しています。この値はデータの長さから自動的に計算されています。
Value of test-statistic is: 0.1691
こちらがKPSS検定の検定統計量です。この値が大きいほど、データが帰無仮説である「定常性」から逸脱していることを意味します。
Critical value for a significance level of:
検定の判断基準となる棄却限界値（Critical Value）の表です。
- 10pct: 有意水準10%の棄却限界値は 0.347 です。
- 5pct: 有意水準5%の棄却限界値は 0.463 です。
- 2.5pct: 有意水準2.5%の棄却限界値は 0.574 です。
- 1pct: 有意水準1%の棄却限界値は 0.739 です。

結論の導出

KPSS検定は、帰無仮説が「定常性」であるため、ADF/PP検定とは逆の判断ルールを用います。

帰無仮説 (H₀): データは水準定常である。
対立仮説 (H₁): データは単位根を持つ（非定常である）。
判断ルール: 検定統計量 > 棄却限界値 であれば、帰無仮説を棄却する（非定常であると判断する）。

今回の結果を見てみましょう。

検定統計量: 0.1691
5%棄却限界値: 0.463

0.1691 < 0.463ですので、検定統計量は棄却限界値を下回っています。

ですので、帰無仮説「データは水準定常である」を棄却することはできません。

総合的な結論

検定統計量が棄却限界値を下回ったため、帰無仮説（水準定常）は棄却できません。

この検定結果は、データが水準定常であるという仮説と矛盾しないことを示しています。今回のデータは実際に水準定常な時系列として生成したものですので、KPSS検定がデータの性質を捉えていることを確認できます。

# --- ケース2: 単位根データ ---
cat("--- ケース2：単位根データに type='mu' で検定 ---\n")
# データは非定常ですので、帰無仮説「水準定常である」は棄却されると予測されます。
# つまり、検定統計量が棄却限界値を上回ると予測されます。
kpss_result2 <- ur.kpss(data_unit_root, type = "mu")
summary(kpss_result2)

--- ケース2：単位根データに type='mu' で検定 ---

####################### 
# KPSS Unit Root Test # 
####################### 

Test is of type: mu with 5 lags. 

Value of test-statistic is: 2.2445 

Critical value for a significance level of: 
                10pct  5pct 2.5pct  1pct
critical values 0.347 0.463  0.574 0.739

`ur.kpss`検定結果の確認

この出力は、非定常な単位根過程として生成された data_unit_root に対して、type="mu"（水準定常性）を帰無仮説としてKPSS検定を実行した結果です。

####################### 
# KPSS Unit Root Test # 
####################### 

Test is of type: mu with 5 lags. 

Value of test-statistic is: 4.1598 

Critical value for a significance level of: 
                10pct  5pct 2.5pct  1pct
critical values 0.347 0.463  0.574 0.739

各項目の確認

KPSS Unit Root Test
実行された検定がKPSS単位根検定であることを示しています。
Test is of type: mu with 5 lags.
検定の前提条件を示しています。
- type: mu: 帰無仮説が水準定常性（データは一定の平均値μの周りで変動する）であることを意味します。
- with 5 lags: 検定統計量の計算に使用されたラグの切り捨てパラメータが5であることを示しています。
Value of test-statistic is: 4.1598
こちらがKPSS検定の検定統計量です。この値が大きいほど、データが帰無仮説である「定常性」から逸脱していることを意味します。
Critical value for a significance level of:
検定の判断基準となる棄却限界値（Critical Value）の表です。
- 10pct: 有意水準10%の棄却限界値は 0.347 です。
- 5pct: 有意水準5%の棄却限界値は 0.463 です。
- 2.5pct: 有意水準2.5%の棄却限界値は 0.574 です。
- 1pct: 有意水準1%の棄却限界値は 0.739 です。

結論の導出

KPSS検定の判断ルールを再度確認します。

帰無仮説 (H₀): データは水準定常である。
対立仮説 (H₁): データは単位根を持つ（非定常である）。
判断ルール: 検定統計量 > 棄却限界値 であれば、帰無仮説を棄却する（非定常であると判断する）。

今回の結果を見てみましょう。

検定統計量: 4.1598
5%棄却限界値: 0.463

4.1598 > 0.463ですので、検定統計量は棄却限界値を上回っています。

ですので、帰無仮説「データは水準定常である」は、5%の有意水準で棄却されます。

この検定結果は、対立仮説である「データは単位根を持つ（非定常である）」ことを支持します。今回のデータは実際に非定常な単位根過程として生成したものですので、KPSS検定が「このデータは定常である」という帰無仮説を否定し、データの非定常な性質を捉えていることを確認できます。

# --- ケース3: トレンド定常データ ---
cat("--- ケース3：トレンド定常データに type='tau' で検定 ---\n")
# データはトレンド定常ですので、帰無仮説「トレンド定常である」は棄却されないと予測されます。
kpss_result3 <- ur.kpss(data_trend_stationary, type = "tau")
summary(kpss_result3)

--- ケース3：トレンド定常データに type='tau' で検定 ---

####################### 
# KPSS Unit Root Test # 
####################### 

Test is of type: tau with 5 lags. 

Value of test-statistic is: 0.0854 

Critical value for a significance level of: 
                10pct  5pct 2.5pct  1pct
critical values 0.119 0.146  0.176 0.216

`ur.kpss`検定結果の確認

この出力は、トレンド定常な過程として生成された data_trend_stationary に対して、type="tau"（トレンド定常性）を帰無仮説としてKPSS検定を実行した結果です。

####################### 
# KPSS Unit Root Test # 
####################### 

Test is of type: tau with 5 lags. 

Value of test-statistic is: 0.0754 

Critical value for a significance level of: 
                10pct  5pct 2.5pct  1pct
critical values 0.119 0.146  0.176 0.216

各項目の確認

KPSS Unit Root Test
実行された検定がKPSS単位根検定であることを示しています。
Test is of type: tau with 5 lags.
検定の前提条件を示しています。
- type: tau: 帰無仮説がトレンド定常性（データは時間トレンドτの周りで変動する）であることを意味します。
- with 5 lags: 検定統計量の計算に使用されたラグの切り捨てパラメータが5であることを示しています。
Value of test-statistic is: 0.0754
こちらがKPSS検定の検定統計量です。この値が小さいほど、データが帰無仮説である「トレンド定常性」と整合的であることを意味します。
Critical value for a significance level of:
検定の判断基準となる棄却限界値（Critical Value）の表です。
- 10pct: 有意水準10%の棄却限界値は 0.119 です。
- 5pct: 有意水準5%の棄却限界値は 0.146 です。
- 2.5pct: 有意水準2.5%の棄却限界値は 0.176 です。
- 1pct: 有意水準1%の棄却限界値は 0.216 です。

結論の導出

KPSS検定の判断ルールを再度確認します。

帰無仮説 (H₀): データはトレンド定常である。
対立仮説 (H₁): データは単位根を持つ（非定常である）。
判断ルール: 検定統計量 > 棄却限界値 であれば、帰無仮説を棄却する（非定常であると判断する）。

今回の結果を見てみましょう。

検定統計量: 0.0754
5%棄却限界値: 0.146

0.0754 < 0.146ですので、検定統計量は棄却限界値を下回っています。

ですので、帰無仮説「データはトレンド定常である」を棄却することはできません。

この検定結果は、データがトレンド定常であるという仮説と矛盾しないことを示しています。今回のデータは実際にトレンド定常な時系列として生成したものですので、KPSS検定がデータの性質を捉えていることを確認できます。

# --- ケース4: ドリフト付き単位根データ ---
cat("--- ケース4：ドリフト付き単位根データに type='tau' で検定 ---\n")
# データは非定常ですので、帰無仮説「トレンド定常である」は棄却されると予測されます。
kpss_result4 <- ur.kpss(data_unit_root_drift, type = "tau")
summary(kpss_result4)

--- ケース4：ドリフト付き単位根データに type='tau' で検定 ---

####################### 
# KPSS Unit Root Test # 
####################### 

Test is of type: tau with 5 lags. 

Value of test-statistic is: 0.9004 

Critical value for a significance level of: 
                10pct  5pct 2.5pct  1pct
critical values 0.119 0.146  0.176 0.216

`ur.kpss`検定結果の確認

この出力は、非定常なドリフト付き単位根過程として生成された data_unit_root_drift に対して、type="tau"（トレンド定常性）を帰無仮説としてKPSS検定を実行した結果です。

####################### 
# KPSS Unit Root Test # 
####################### 

Test is of type: tau with 5 lags. 

Value of test-statistic is: 0.955 

Critical value for a significance level of: 
                10pct  5pct 2.5pct  1pct
critical values 0.119 0.146  0.176 0.216

各項目の確認

KPSS Unit Root Test
実行された検定がKPSS単位根検定であることを示しています。
Test is of type: tau with 5 lags.
検定の前提条件を示しています。
- type: tau: 帰無仮説がトレンド定常性（データは時間トレンドτの周りで変動する）であることを意味します。
- with 5 lags: 検定統計量の計算に使用されたラグの切り捨てパラメータが5であることを示しています。
Value of test-statistic is: 0.955
こちらがKPSS検定の検定統計量です。この値が大きいほど、データが帰無仮説である「トレンド定常性」から逸脱していることを意味します。
Critical value for a significance level of:
検定の判断基準となる棄却限界値（Critical Value）の表です。
- 10pct: 有意水準10%の棄却限界値は 0.119 です。
- 5pct: 有意水準5%の棄却限界値は 0.146 です。
- 2.5pct: 有意水準2.5%の棄却限界値は 0.176 です。
- 1pct: 有意水準1%の棄却限界値は 0.216 です。

結論の導出

KPSS検定の判断ルールを再度確認します。

帰無仮説 (H₀): データはトレンド定常である。
対立仮説 (H₁): データは単位根を持つ（非定常である）。
判断ルール: 検定統計量 > 棄却限界値 であれば、帰無仮説を棄却する（非定常であると判断する）。

今回の結果を見てみましょう。

検定統計量: 0.955
5%棄却限界値: 0.146

0.955 > 0.146ですので、検定統計量は棄却限界値を上回っています。

ですので、帰無仮説「データはトレンド定常である」は、5%の有意水準で棄却されます。

総合的な結論

帰無仮説（トレンド定常性）が棄却されたため、対立仮説（単位根の存在）が支持されます。

この検定結果は、「この時系列データは非定常である」という結論を支持します。今回のデータは実際に非定常なドリフト付き単位根過程として生成したものですので、KPSS検定がデータの非定常な性質を捉えていることを確認できます。

以上です。

ur.kpss関数について

ur.kpss関数の引数について

y

type

lags

use.lag

シミュレーション

ur.kpss検定結果の確認

各項目の確認

結論の導出

総合的な結論

ur.kpss検定結果の確認

各項目の確認

結論の導出

ur.kpss検定結果の確認

各項目の確認

結論の導出

ur.kpss検定結果の確認

各項目の確認

結論の導出

総合的な結論

`y`

`type`

`lags`

`use.lag`

`ur.kpss`検定結果の確認

`ur.kpss`検定結果の確認

`ur.kpss`検定結果の確認

`ur.kpss`検定結果の確認