Rの関数 ur.ers {urca} のスクラッチ再現を試みます。
本ポストはこちらの続きです。

Rの関数:ur.ers {urca}
Rの関数から ur.ers {urca} を確認します。本ポストはこちらの続きです。ur.ers関数についてur.ersは、エリオット–ローゼンバーグ–ストック(Elliot, Rothenberg, and Stock, ERS)検定 を...
ur.ers(type=“DF-GLS”, model=“trend”) のスクラッチ再現コード
# ============================================================
# ur.ers(type="DF-GLS", model="trend") のスクラッチ再現コード
# (Elliott, Rothenberg, and Stock (1996) の DF-GLS 検定)
# ============================================================
library(urca)
# -------------------------------
# (1) データ生成
# -------------------------------
seed <- 20251017
set.seed(seed)
T <- 100 # サンプルサイズ
phi <- 0.95 # AR(1) 系列の係数(単位根に近い)
e <- rnorm(T) # ホワイトノイズ
y <- numeric(T)
for (t in 2:T) y[t] <- phi * y[t - 1] + e[t] # y_t = phi * y_{t-1} + e_t
# -------------------------------
# (2) ur.ers() によるERS単位根検定
# -------------------------------
ur_out <- ur.ers(y, type = "DF-GLS", model = "trend", lag.max = 4)
urca_t <- ur_out@teststat # t値(DF-GLS統計量)
lag_used <- ur_out@lag # ur.ersが自動選択したラグ数
# ============================================================
# (3) ur.ers() の理論構造に基づくスクラッチ実装
# ============================================================
# -------------------------------
# 3-1. GLS 前処理:局所デトレンド
# -------------------------------
# Elliott et al. (1996) では、GLSデトレンドのために
# (1 - a_hat * L) で前処理を行う。
# a_hat = 1 - c/T
# - c = 13.5(モデルに定数+トレンドを含む場合)
# - c = 7(モデルが定数のみの場合)
# ur.ers() ではこの規則を採用している。
# ------------------------------------------------------------
ahat <- 1 - 13.5 / T
trd <- 1:T # 時間トレンド
# y_t のGLS変換: y_t^a = y_t - a_hat * y_{t-1} (ただし先頭はそのまま)
ya <- c(y[1], y[2:T] - ahat * y[1:(T - 1)])
# 定数項・トレンド項も同様にGLS変換
za1 <- c(1, rep(1 - ahat, T - 1)) # 定数項(1)
za2 <- c(1, trd[2:T] - ahat * trd[1:(T - 1)]) # トレンド項(t)
# -------------------------------
# 3-2. GLS回帰による定数除去(デトレンド)
# -------------------------------
# ya = β1 * za1 + β2 * za2 + u_t
# 切片を含めず回帰(-1)とする理由:
# za1, za2が既に「定数項・トレンド項」として設計されているため。
# ------------------------------------------------------------
yd.reg <- lm(ya ~ -1 + za1 + za2)
# 推定された β1, β2 を使って y からトレンドを除去
coef_hat <- coef(yd.reg)
yd <- y - coef_hat[1] - coef_hat[2] * trd
# → これが GLS デトレンド済み系列(ur.ers内部の "detrended series")
# -------------------------------
# 3-3. DF-GLS 検定用のADF回帰を構築
# -------------------------------
# Δyd_t = ρ * yd_{t-1} + Σ γ_i * Δyd_{t-i} + ε_t
# の回帰を行い、ρ の t値をDF-GLS統計量とする。
# ------------------------------------------------------------
yd.l <- yd[1:(T - 1)] # 遅行系列 yd_{t-1}
yd.diff <- diff(yd) # 差分系列 Δyd_t
p <- lag_used # ur.ers()が自動選択したラグ数を使用
if (p > 0) {
# embed() によりラグ項行列を作成
# embed(diff(yd), p+1) の結果は Δyd_t, Δyd_{t-1}, …, Δyd_{t-p}
# ここから Δyd_t(最初の列)を除いた部分を説明変数として使用
yd.dlags <- embed(diff(yd), p + 1)[, -1]
# データフレーム整形
data.dfgls <- data.frame(
yd.diff = yd.diff[-(1:p)], # 先頭p観測を除外
yd.l = yd.l[-(1:p)], # 遅行系列(整列)
yd.dlags
)
colnames(data.dfgls)[-(1:2)] <- paste0("yd.diff.lag", 1:p)
# 回帰式: Δyd_t ~ yd_{t-1} + Δyd_{t-1} + … + Δyd_{t-p} (切片なし)
dfgls.form <- as.formula(paste(
"yd.diff ~ -1 +", paste(colnames(data.dfgls)[-1], collapse = "+")
))
} else {
# ラグなしADF
data.dfgls <- data.frame(yd.diff = yd.diff, yd.l = yd.l)
dfgls.form <- yd.diff ~ -1 + yd.l
}
# -------------------------------
# 3-4. OLS回帰と統計量抽出
# -------------------------------
dfgls.reg <- summary(lm(dfgls.form, data = data.dfgls))
scratch_t <- coef(dfgls.reg)[1, 3] # yd_{t-1} の t値が検定統計量
# -------------------------------
# (4) 結果比較
# -------------------------------
cat("スクラッチ実装により求めた検定統計量 t:", scratch_t, "\n")
cat("関数ur.ers()により求めた検定統計量 t:", urca_t, "\n")
cat("両者は一致しているか:", all.equal(scratch_t, urca_t), "\n")スクラッチ実装により求めた検定統計量 t: -1.482571
関数ur.ers()により求めた検定統計量 t: -1.482571
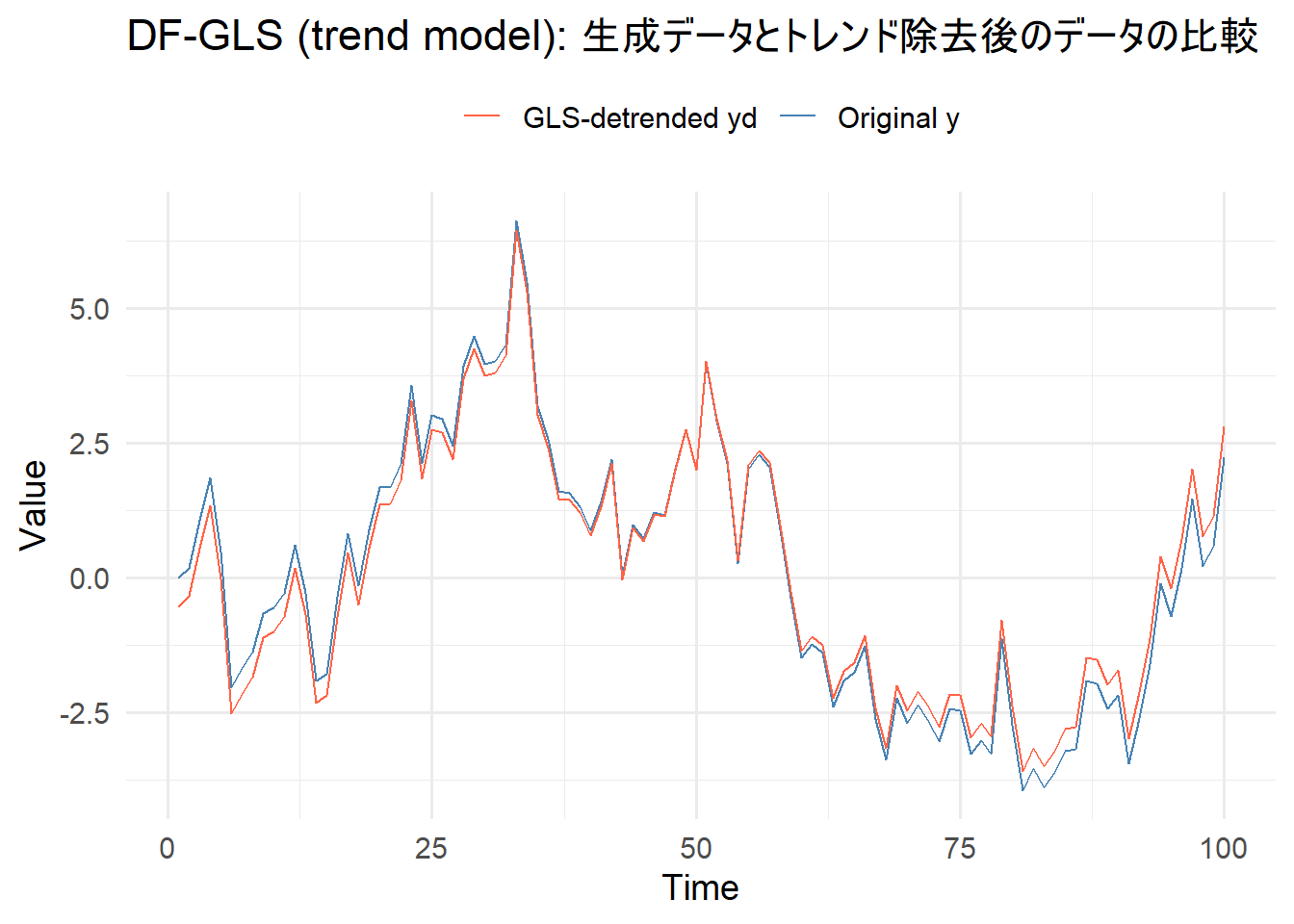
両者は一致しているか: TRUE 続いて、生成したサンプル時系列データ(Original y)とトレンド除去後の時系列データ(GLS_detrended_yd)を比較します。
library(ggplot2)
df_plot <- data.frame(
t = 1:T,
y = y,
yd = yd
)
ggplot(df_plot, aes(x = t)) +
geom_line(aes(y = y, color = "Original y"), linewidth = 0.5) +
geom_line(aes(y = yd, color = "GLS-detrended yd"), linewidth = 0.5) +
scale_color_manual(values = c("Original y" = "steelblue", "GLS-detrended yd" = "tomato")) +
labs(
title = "DF-GLS (trend model): 生成データとトレンド除去後のデータの比較",
x = "Time", y = "Value", color = ""
) +
theme_minimal(base_size = 14) +
theme(legend.position = "top")ur.ers(type=“DF-GLS”, model=“constant”) のスクラッチ再現コード
# ============================================================
# ur.ers(type="DF-GLS", model="constant") のスクラッチ再現コード
# Elliott, Rothenberg, and Stock (1996) のDF-GLS検定
# ============================================================
# -------------------------------
# (1) データ生成
# -------------------------------
# 先に生成したサンプル時系列データ y を利用。
# -------------------------------
# (2) ur.ers() によるERS単位根検定
# -------------------------------
ur_out <- ur.ers(y, type = "DF-GLS", model = "constant", lag.max = 4)
urca_t <- ur_out@teststat # DF-GLS統計量(t値)
lag_used <- ur_out@lag # 自動選択されたラグ数
# ============================================================
# (3) ur.ers() の理論構造に基づくスクラッチ実装
# ============================================================
# -------------------------------
# 3-1. GLSデトレンド準備
# -------------------------------
# Elliott et al. (1996) の提案では、GLS変換係数 a_hat は:
# a_hat = 1 - c / T
# - model="constant" の場合: c = 7
# - model="trend" の場合: c = 13.5
# ur.ers() もこの値を採用している。
# ------------------------------------------------------------
ahat <- 1 - 7 / T # 定数項モデルでは c = 7
# GLS変換を行う:
# y_t^a = y_t - a_hat * y_{t-1} (ただし先頭はそのまま)
ya <- c(y[1], y[2:T] - ahat * y[1:(T - 1)])
# 定数項(1)のGLS変換:
# z_t^a = 1 - a_hat * 1 = 1 - a_hat
# ただし t = 1 の場合は 1 とする
za1 <- c(1, rep(1 - ahat, T - 1))
# -------------------------------
# 3-2. GLS回帰による定数除去(デトレンド)
# -------------------------------
# ya = β1 * za1 + u_t
# (切片なし回帰:-1を指定)
# ------------------------------------------------------------
yd.reg <- lm(ya ~ -1 + za1)
# 推定された β1 を使って元系列 y から定数成分を除去
coef_hat <- coef(yd.reg)
yd <- y - coef_hat[1]
# → これが「GLSデトレンド済み系列(DF-GLS系列)」に相当
# -------------------------------
# 3-3. DF-GLS 検定用のADF回帰を構築
# -------------------------------
# DF-GLSの検定回帰式:
# Δyd_t = ρ * yd_{t-1} + Σ γ_i * Δyd_{t-i} + ε_t
# ------------------------------------------------------------
yd.l <- yd[1:(T - 1)] # yd_{t-1}
yd.diff <- diff(yd) # Δyd_t
p <- lag_used # ur.ersが選択したラグ数
if (p > 0) {
# Δyd のラグ項を生成(embedで時系列行列を作成)
yd.dlags <- embed(diff(yd), p + 1)[, -1]
# データ整形
data.dfgls <- data.frame(
yd.diff = yd.diff[-(1:p)],
yd.l = yd.l[-(1:p)],
yd.dlags
)
colnames(data.dfgls)[-(1:2)] <- paste0("yd.diff.lag", 1:p)
# 回帰式を動的に構築
dfgls.form <- as.formula(paste(
"yd.diff ~ -1 +", paste(colnames(data.dfgls)[-1], collapse = "+")
))
} else {
# ラグなしADF
data.dfgls <- data.frame(yd.diff = yd.diff, yd.l = yd.l)
dfgls.form <- yd.diff ~ -1 + yd.l
}
# -------------------------------
# 3-4. OLS回帰と統計量抽出
# -------------------------------
dfgls.reg <- summary(lm(dfgls.form, data = data.dfgls))
scratch_t <- coef(dfgls.reg)[1, 3] # yd_{t-1} の t値を抽出
# -------------------------------
# (4) 結果比較
# -------------------------------
cat("スクラッチ実装により求めた検定統計量 t:", scratch_t, "\n")
cat("関数ur.ers()により求めた検定統計量 t:", urca_t, "\n")
cat("両者は一致しているか:", all.equal(scratch_t, urca_t), "\n")スクラッチ実装により求めた検定統計量 t: -1.465639
関数ur.ers()により求めた検定統計量 t: -1.465639
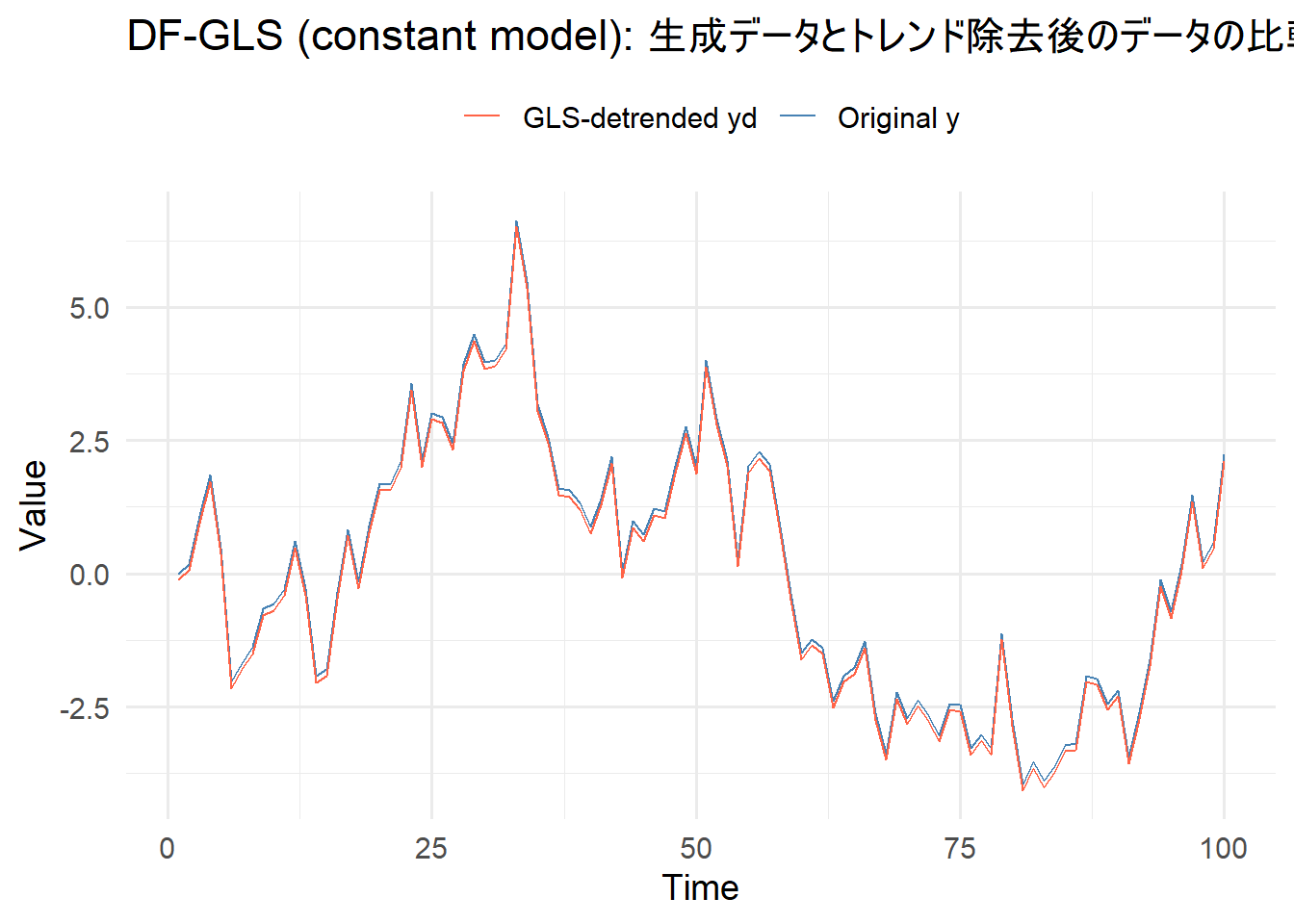
両者は一致しているか: TRUE 続いて、生成したサンプル時系列データ(Original y)とトレンド除去後の時系列データ(GLS_detrended_yd)を比較します。
df_plot <- data.frame(
t = 1:T,
y = y,
yd = yd
)
ggplot(df_plot, aes(x = t)) +
geom_line(aes(y = y, color = "Original y"), linewidth = 0.5) +
geom_line(aes(y = yd, color = "GLS-detrended yd"), linewidth = 0.5) +
scale_color_manual(values = c("Original y" = "steelblue", "GLS-detrended yd" = "tomato")) +
labs(
title = "DF-GLS (constant model): 生成データとトレンド除去後のデータの比較",
x = "Time", y = "Value", color = ""
) +
theme_minimal(base_size = 14) +
theme(legend.position = "top")以上です。