Rの関数:RM {eRm}

Rの関数から RM {eRm} を確認します。

`RM`関数とは

eRmパッケージのRM関数は、二値の項目反応データ（例：正解・不正解、はい・いいえ）を分析するための、ラッシュモデル（Rasch Model）を推定する関数です。

ラッシュモデルは項目反応理論（Item Response Theory, IRT）の基本的なモデルの一つであり、個人の能力（θ, theta）と、各項目が持つ固有の困難度（β, beta）の二つのパラメータを用いて、個人が特定の項目に正答する確率をモデル化します。

本関数は、条件付き最尤推定（Conditional Maximum Likelihood, CML）法を用いて項目の困難度パラメータを推定します。

CML法は、個人の能力パラメータを推定の過程で除去（sum out）するため、項目の困難度パラメータをより正確に、かつサンプルサイズに依存しにくい形で推定できるという利点があります。

推定されたモデルからは、各項目の困難度やその標準誤差、モデルの対数尤度などが得られ、モデルの適合度を評価するための様々な関連関数（例：LRtest, Waldtest）も利用できます。

`RM`関数の引数

RM関数は以下の引数を取ります。

library(eRm)
args(RM)

function (X, W, se = TRUE, sum0 = TRUE, etaStart) 
NULL

X
- 回答データ行列。行が個人（受験者）、列が項目（問題）を表す0と1からなる行列です。1は正答、0は誤答を意味します。欠損値は NA として含めることが可能です。
W
- デザイン行列。これはラッシュモデルをより複雑な線形ラッシュモデル（例：LLTM）に拡張する際に使用される行列です。通常のラッシュモデルを推定する場合は、この引数を省略できます。省略した場合、関数が自動的に標準的なデザイン行列を生成します。
se
- 標準誤差の計算。TRUE（デフォルト）に設定すると、推定されたパラメータの標準誤差が計算されます。FALSEにすると計算が省略され、処理がわずかに速くなります。
sum0
- パラメータの制約。TRUE（デフォルト）に設定すると、項目の困難度パラメータ（β）の合計が0になるように制約（sum-to-zero constraint）が課せられます。FALSEに設定すると、最初の項目の困難度パラメータが0に固定されます。どちらの制約を用いてもモデルの本質は変わりませんが、パラメータの解釈が異なります。
etaStart
- パラメータ推定の初期値。モデルのパラメータを推定する際の、数値最適化アルゴリズムの初期値をベクトルで指定します。省略可能で、その場合は0ベクトルが初期値として使用されます。

シミュレーションによる `RM` 関数の確認

ラッシュモデルに従うサンプルデータを作成し、シミュレーションを実行します。

1. サンプルデータの作成

まず、シミュレーションの土台となるデータを作成します。ここでは、200人の受験者が15項目のテストに回答した状況を想定します。個人の能力（theta）と項目の困難度（beta）は、それぞれ正規分布から生成します。

ラッシュモデルによれば、個人 p が項目 i に正答する確率 P(X_pi = 1) は以下の式で与えられます。

P(X_pi = 1) = exp(theta_p - beta_i) / (1 + exp(theta_p - beta_i))

この確率式に基づいて、0か1の回答データを生成します。

# パッケージの読み込み
library(eRm)

# 再現性のための乱数シード設定
seed <- 20251105
set.seed(seed)

# シミュレーションのパラメータ設定
n_persons <- 200 # 受験者数
n_items <- 15 # 項目数

# 真のパラメータを生成
# 個人の能力パラメータ (theta) を標準正規分布から生成
true_theta <- rnorm(n_persons, mean = 0, sd = 1.5)
# 項目の困難度パラメータ (beta) を正規分布から生成
true_beta <- rnorm(n_items, mean = 0, sd = 1.0)
# sum0制約を満たすように調整
true_beta <- true_beta - mean(true_beta)

# 回答データを格納する行列を準備
sim_data <- matrix(NA, nrow = n_persons, ncol = n_items)
colnames(sim_data) <- paste0("Item", 1:n_items)
rownames(sim_data) <- paste0("Person", 1:n_persons)

# ラッシュモデルに基づいて回答データを生成
for (p in 1:n_persons) {
  for (i in 1:n_items) {
    # 正答確率を計算
    prob <- exp(true_theta[p] - true_beta[i]) / (1 + exp(true_theta[p] - true_beta[i]))
    # 確率に基づいて0か1を生成
    sim_data[p, i] <- rbinom(1, 1, prob)
  }
}

# 作成したデータの最初の部分を表示
cat("--- 生成されたサンプルデータの一部を確認 ---\n")
print(head(sim_data))

--- 生成されたサンプルデータの一部を確認 ---
        Item1 Item2 Item3 Item4 Item5 Item6 Item7 Item8 Item9 Item10 Item11 Item12 Item13 Item14 Item15
Person1     0     1     0     0     0     0     0     0     0      0      0      0      1      0      1
Person2     1     1     1     0     0     0     0     0     0      0      0      0      0      0      0
Person3     0     0     0     0     0     0     0     0     0      1      0      0      0      0      0
Person4     1     0     0     0     0     0     1     0     1      0      0      0      0      0      1
Person5     0     0     1     0     1     0     0     1     1      0      0      0      1      0      1
Person6     1     1     0     0     0     0     0     1     1      0      1      0      0      0      0

2. `RM`関数によるラッシュモデルの推定

次に、生成した sim_data を用いて RM 関数を実行し、ラッシュモデルを推定します。

summary() 関数を使うことで、推定された項目の困難度パラメータやその標準誤差、対数尤度などの詳細な結果を確認できます。

# RM関数を用いてラッシュモデルを推定
# sum0 = TRUE はデフォルトですが、明示的に指定しています
model_fit <- RM(sim_data, sum0 = TRUE)

# 推定結果の要約を表示
cat("--- RM関数の推定結果の要約 ---\n")
summary(model_fit)

--- RM関数の推定結果の要約 ---

Results of RM estimation: 

Call:  RM(X = sim_data, sum0 = TRUE) 

Conditional log-likelihood: -1080.993 
Number of iterations: 14 
Number of parameters: 14 

Item (Category) Difficulty Parameters (eta): with 0.95 CI:
       Estimate Std. Error lower CI upper CI
Item2    -0.319      0.165   -0.642    0.003
Item3    -0.205      0.165   -0.527    0.118
Item4     1.662      0.198    1.273    2.051
Item5     0.924      0.178    0.575    1.273
Item6     0.202      0.167   -0.125    0.530
Item7     1.131      0.183    0.772    1.489
Item8     0.382      0.169    0.051    0.713
Item9    -0.463      0.165   -0.786   -0.140
Item10   -1.903      0.195   -2.285   -1.521
Item11    0.262      0.168   -0.066    0.590
Item12   -0.434      0.165   -0.757   -0.111
Item13   -0.291      0.165   -0.613    0.032
Item14    1.061      0.181    0.706    1.416
Item15   -1.604      0.184   -1.965   -1.244

Item Easiness Parameters (beta) with 0.95 CI:
            Estimate Std. Error lower CI upper CI
beta Item1     0.405      0.165    0.083    0.728
beta Item2     0.319      0.165   -0.003    0.642
beta Item3     0.205      0.165   -0.118    0.527
beta Item4    -1.662      0.198   -2.051   -1.273
beta Item5    -0.924      0.178   -1.273   -0.575
beta Item6    -0.202      0.167   -0.530    0.125
beta Item7    -1.131      0.183   -1.489   -0.772
beta Item8    -0.382      0.169   -0.713   -0.051
beta Item9     0.463      0.165    0.140    0.786
beta Item10    1.903      0.195    1.521    2.285
beta Item11   -0.262      0.168   -0.590    0.066
beta Item12    0.434      0.165    0.111    0.757
beta Item13    0.291      0.165   -0.032    0.613
beta Item14   -1.061      0.181   -1.416   -0.706
beta Item15    1.604      0.184    1.244    1.965

本出力は、RM関数によってラッシュモデルを推定した結果の要約です。

シミュレーションで生成したsim_dataに対して、モデルがどのように適合し、各項目の特性がどのように推定されたかを示しています。

1. モデルの全体情報

Results of RM estimation: 

Call:  RM(X = sim_data, sum0 = TRUE) 

Conditional log-likelihood: -1080.993 
Number of iterations: 14 
Number of parameters: 14

Call:
- この行は、本結果を生成するために実行された関数呼び出しをそのまま示しています。sim_data を入力データとして、sum0 = TRUE の制約（全項目パラメータの合計を0にする）の下で RM 関数が実行されたことを示しています。
Conditional log-likelihood: -1080.993
- 本数値は「条件付き対数尤度」と呼ばれる値で、モデルのデータへの適合度を表す指標です。条件付き最尤推定（CML）法では、個人の能力に依存しない条件付きの尤度を最大化します。異なるモデル間での適合度を比較する際（例えば LRtest 関数を用いる場合）に基準となります。
Number of iterations: 14
- パラメータを推定するための数値最適化アルゴリズムが、収束するまでにかかった反復計算の回数です。14回という少ない回数で収束していることから、推定プロセスがスムーズに進んだことがわかります。
Number of parameters: 14
- モデルで推定されたパラメータの数です。項目数は15個ですが、sum0 = TRUE 制約により、全パラメータの合計が0になるように調整されています。それゆえ、14個のパラメータが自由に値を決めれば、残りの1個のパラメータは自動的に決まるため、独立したパラメータの数は14個となります。

2. 項目パラメータの推定結果

eRmパッケージは、同じ項目特性を「困難度（Difficulty）」と「易しさ（Easiness）」という2つの視点から表示します。これらは符号が反転しただけの、完全に同じ情報です。

(注意)

RM関数では、Difficulty Parameters は eta、その正反対である Easiness Parameters は beta として扱われています。

よって、前述しました 項目の困難度（beta） と、summary関数中の beta とは符号が正反対になりますことに留意してください。

`Item (Category) Difficulty Parameters (eta):`

こちらは、パラメータを困難度として解釈した結果です。値が大きいほど項目が難しいことを意味します。

       Estimate Std. Error lower CI upper CI
Item4     1.662      0.198    1.273    2.051
...
Item10   -1.903      0.195   -2.285   -1.521

Estimate: 各項目の困難度パラメータの推定値です。
- 例: Item4の推定値は 1.662 であり、最も大きい正の値です。それゆえ、このテストの中で最も難しい項目であると解釈できます。
- 例: Item10の推定値は -1.903 であり、最も小さい負の値です。それゆえ、このテストの中で最も易しい項目であると解釈できます。
- なお、RM(..., sum0 = TRUE) の制約を設けていますので Item1 は表示されていません。Item2 から Item15 までの Estimate の合計を 1から減じた結果が、Item1 の Estimate になります。
Std. Error:
- 標準誤差。推定値の精度（ばらつきの小ささ）を示します。値が小さいほど、推定がより正確であることを意味します。
lower CI, upper CI:
- 信頼係数95%の信頼区間。真のパラメータ値が95%の確率で含まれると期待される範囲です。例えば Item4 の場合、真の困難度は 1.273 から 2.051 の間にあると推定されます。

`Item Easiness Parameters (beta):`

こちらは、パラメータを易しさとして解釈した結果です。値が大きいほど項目が易しいことを意味します。

            Estimate Std. Error lower CI upper CI
beta Item4    -1.662      0.198   -2.051   -1.273
...
beta Item10    1.903      0.195    1.521    2.285

関係性:
- こちらの Estimate は、上記の困難度 (eta) の符号をちょうど反転させた値になっています (beta = -eta)。
- 例: Item4 の困難度 (eta) が 1.662 であったのに対し、易しさ (beta) は -1.662 となっています。易しさの値が負に大きいことは、その項目が難しいことを意味し、解釈は完全に一致します。
- 例: Item10 の困難度 (eta) が -1.903 であったのに対し、易しさ (beta) は 1.903 となっています。易しさの値が正に大きいことは、その項目が易しいことを意味します。

3. 真のパラメータと推定パラメータの比較

なお、Difficulty Parameters (eta) を coef(model_fit, parm = "eta") により取得すると、Item1 の係数を直接抽出できないため、coef(model_fit, parm = "beta") の結果に -1 を乗じた結果を、推定されたbeta として求めます。

# 推定された beta の符号を反転した結果を 項目困難度パラメータ として抽出
estimated_beta <- -1 * coef(model_fit, parm = "beta")

# 真の困難度と推定された困難度をデータフレームにまとめる
param_comparison <- data.frame(
  True_Beta = true_beta,
  Estimated_Beta = estimated_beta
)

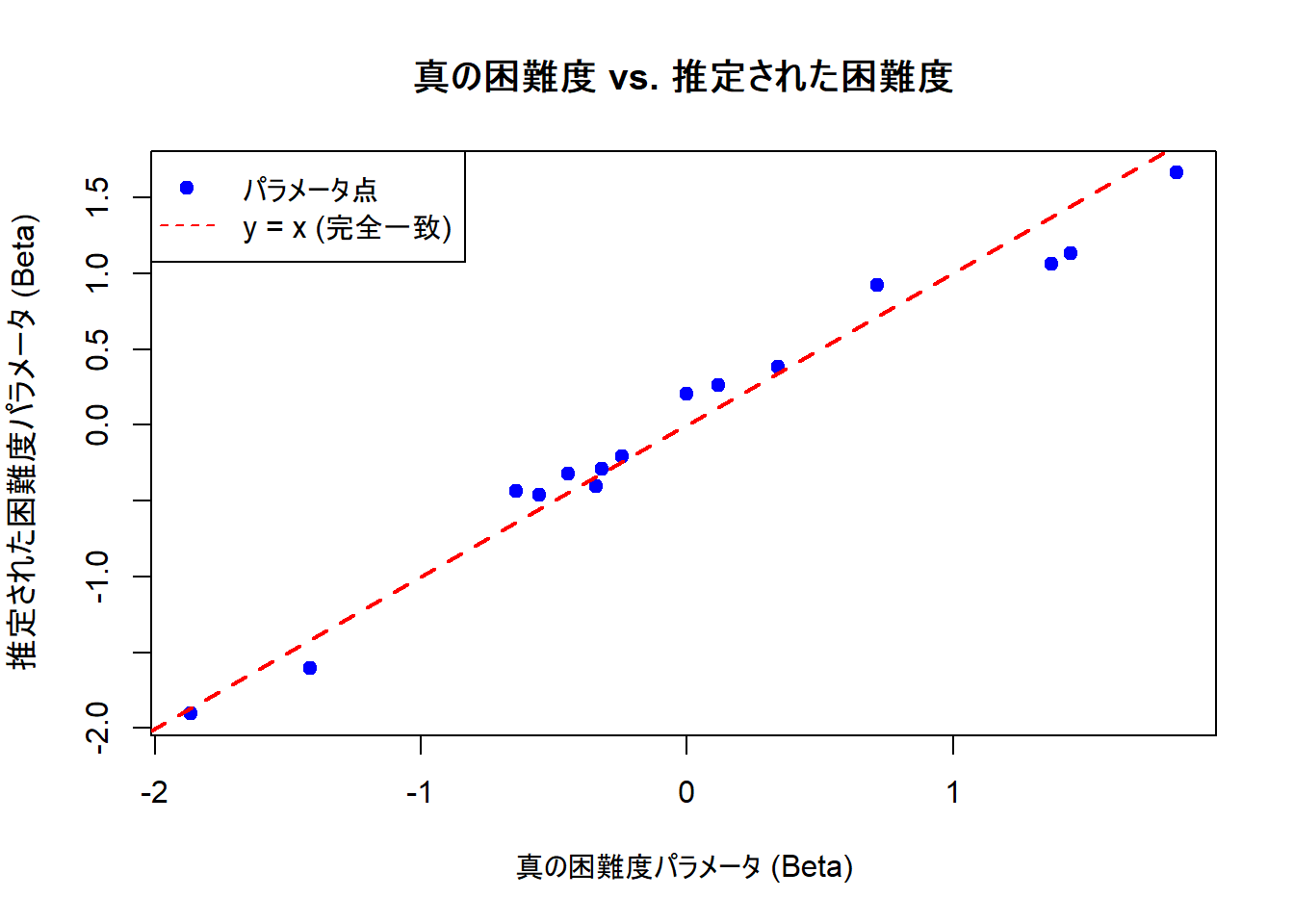
# 散布図を作成して視覚的に比較
plot(param_comparison,
  main = "真の困難度 vs. 推定された困難度",
  xlab = "真の困難度パラメータ (Beta)",
  ylab = "推定された困難度パラメータ (Beta)",
  pch = 19, # プロット点の形状
  col = "blue"
)
# y=xの直線を引く（完全な一致を示す線）
abline(a = 0, b = 1, col = "red", lty = 2, lwd = 2)
legend("topleft",
  legend = c("パラメータ点", "y = x (完全一致)"),
  col = c("blue", "red"),
  pch = c(19, NA),
  lty = c(NA, 2)
)

Figure 1 では、パラメータ点がほぼ赤い破線（y=xの完全一致）の近い位置に並んでいることが確認できます。

4. パーソン・アイテム・マップによる結果の可視化

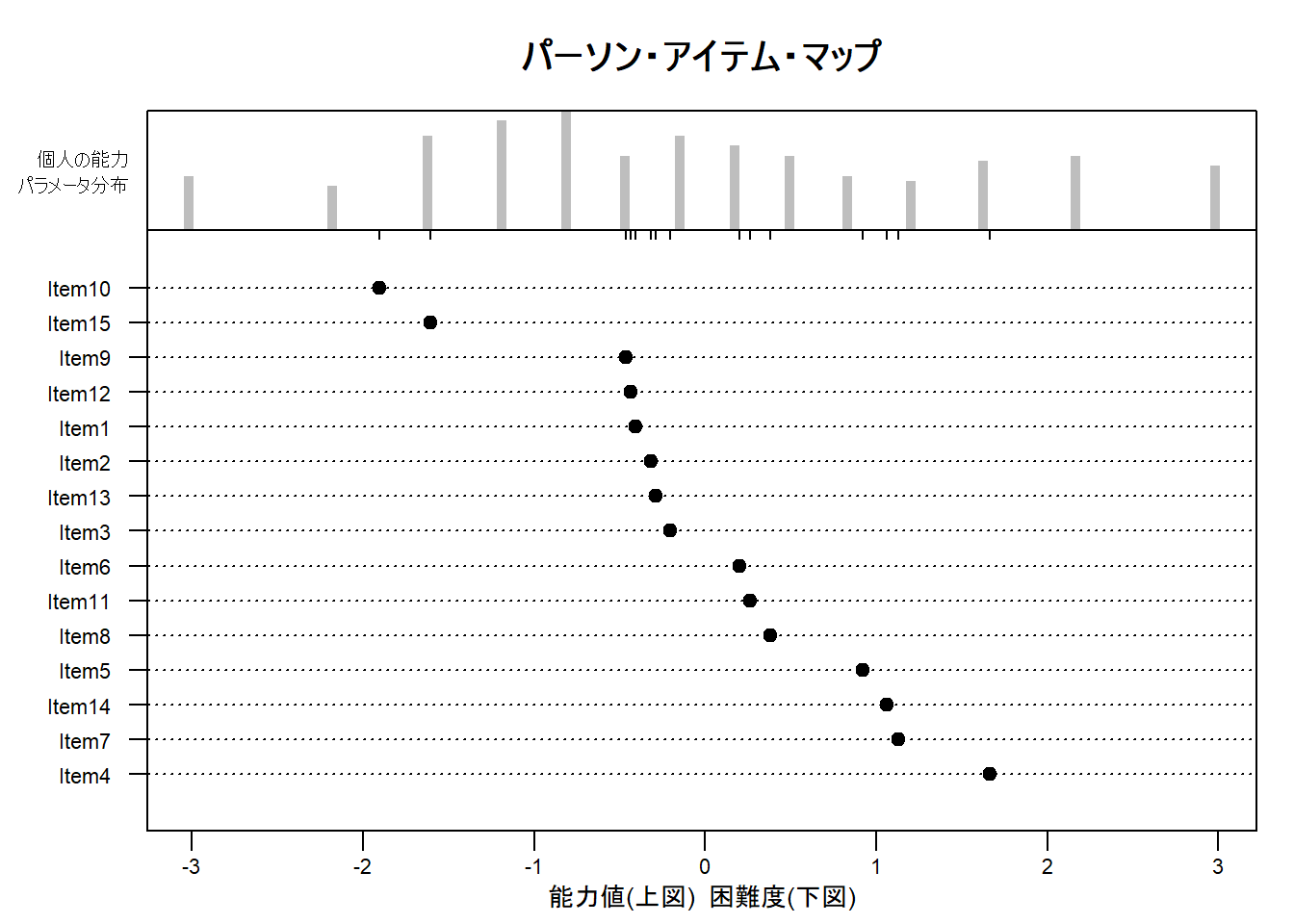
plotPImap() 関数を用いると、推定された個人の能力と項目の困難度を同じ尺度上にプロットした「パーソン・アイテム・マップ」を作成できます。

このマップは、受験者集団の能力分布に対して、テストが適切な難易度範囲をカバーしているかを評価するのに役立ちます。

# パーソン・アイテム・マップを描画
# sorted = TRUE で項目を困難度順に並べ替える
plotPImap(model_fit,
  sorted = TRUE,
  main = "パーソン・アイテム・マップ",
  latdim = "能力値(上図)  困難度(下図)",
  pplabel = "個人の能力\nパラメータ分布"
)

Figure 2 は、個人の能力と項目の困難度という、本来は直接観測できない2つの潜在的な特性を、共通の物差し（尺度） の上に配置して表示します。

Figure 2 により、受験者集団の能力とテストに含まれる項目の難易度の対応関係が確認できます。

Figure 2 は、上下2つの部分から構成されています。

上図：個人の能力分布

何を示しているか:
- 上図のヒストグラム（棒グラフ）は、受験者全員の能力パラメータ (θ) の分布を示しています。横軸が能力の尺度を表し、右に行くほど能力が高いことを意味します。棒の高さは、その能力レベルに該当する受験者の人数（頻度）を表します。
このプロットからわかること:
- このシミュレーションデータでは、受験者の能力は-3から+3程度の範囲に、0付近を中心として広がっていることが見て取れます。これは、能力が正規分布に従うようにデータを生成したため、その特徴が現れています。

下図：項目の困難度分布

何を示しているか:
- 下図には、各項目の困難度パラメータ が黒い点でプロットされています。sorted = TRUE オプションが指定されているため、項目は上から易しい順、下に行くほど難しい順に並べ替えられています。
このプロットからわかること:
- 最も上に位置する Item10（横軸の値が約-1.9）が、このテストの中で最も易しい項目です。
- 最も下に位置する Item4（横軸の値が約+1.7）が、最も難しい項目です。
- その他の項目は、この2つの項目の間の様々な難易度レベルに分布していることがわかります。

マップ全体の解釈：能力と困難度のマッチング

Figure 2 の役割は、上図の「個人の能力分布」と下図の「項目の困難度分布」を比較することです。

基本的な見方:
- ある個人の能力とある項目の困難度が、横軸上の同じ位置にある場合、その個人がその項目に正答する確率は50%となります。もし個人の能力が項目の困難度よりも右にあれば正答率は50%より高くなり、左にあれば50%より低くなります。
テストの評価:
- 適切なターゲティング:
  - Figure 2 を見ると、項目の困難度分布（約-1.9〜+1.7）は、受験者集団の能力分布の中心部分をうまくカバーしています。それゆえ、このテストは、平均的な能力を持つ受験者の能力を測定するのに適していると言えます。
- 測定の限界（天井効果・床効果）:
  - 一方で、能力が非常に高い受験者（ヒストグラムの右端）にとっては、最も難しい Item4 でさえも比較的易しいかもしれません。逆に、能力が非常に低い受験者（左端）にとっては、最も易しい Item10 でさえ難しすぎる可能性があります。このように、テストが受験者の能力レベルに合っていない問題点を視覚的に洗い出すのに Figure 2 は役立ちます。

以上です。

RM関数とは

RM関数の引数

シミュレーションによる RM 関数の確認