Rの関数:lsei {limSolve}

Rの関数から lsei {limSolve} を確認します。

lsei関数とは

lseiは “Least Squares with Equality and Inequality constraints” の略になります。

本関数は、制約条件下で最小二乗問題を解くため関数であり、具体的には、以下の数式で表される問題を解決します。

最小化の対象:

  • ||Ax - B||^2 (Aとxの積とBとの差の二乗和)

制約条件:

  1. 等式制約: Ex = F
  2. 不等式制約: Gx >= H

本関数は、与えられた等式制約と不等式制約を厳密に満たしながら、近似方程式 Ax ≈ B の誤差の二乗和を最小にするようなベクトル x を見つけ出します。

lsei関数の引数

lseiは以下の引数を取ります。

library(limSolve)
args(lsei)
function (A = NULL, B = NULL, E = NULL, F = NULL, G = NULL, H = NULL, 
    Wx = NULL, Wa = NULL, type = 1, tol = sqrt(.Machine$double.eps), 
    tolrank = NULL, fulloutput = FALSE, verbose = TRUE, lower = NULL, 
    upper = NULL) 
NULL
  • A: (matrix or NULL)

    • 最小化したい二乗和 ||Ax - B||^2 を構成する係数行列です。各行が一つの近似式に対応し、各列が未知数 x の各要素に対応します。
  • B: (vector or NULL)

    • 近似方程式 Ax ≈ B の右辺のベクトルです。A の行数と同じ長さでなければなりません。
  • E: (matrix or NULL)

    • 等式制約 Ex = F を構成する係数行列です。この制約は厳密に満たされる必要があります。
  • F: (vector or NULL)

    • 等式制約 Ex = F の右辺のベクトルです。E の行数と同じ長さでなければなりません。
  • G: (matrix or NULL)

    • 不等式制約 Gx >= H を構成する係数行列です。この制約も厳密に満たされる必要があります。
  • H: (vector or NULL)

    • 不等式制約 Gx >= H の右辺のベクトルです。G の行数と同じ長さでなければなりません。
  • Wx: (vector or NULL)

    • 未知数 x の各要素に対する重み付けベクトルです。type = 1 の場合のみ使用可能です。
  • Wa: (vector or NULL)

    • 近似方程式 Ax ≈ B の各行に対する重み付けベクトルです。これにより、特定の方程式の誤差をより重視して最小化できます。
  • type: (integer)

    • 使用する計算アルゴリズムを指定します。
      • type = 1 (デフォルト): limSolveパッケージに組み込まれているFortranのlseiサブルーチンを使用します。これは、HaskellとHansonによるアルゴリズムに基づいています。
      • type = 2: quadprogパッケージのsolve.QP関数を使用します。これは問題を二次計画問題として解きます。
  • tol: (numeric)

    • 数値計算における許容誤差です。特異値分解や制約条件の判定に用いられます。デフォルトは .Machine$double.eps の平方根です。
  • tolrank: (vector or NULL)

    • type = 1 の場合のみ使用されます。等式制約行列と、縮小された最小二乗問題の行列のランクを決定するための許容誤差を2要素のベクトルで指定します。
  • fulloutput: (logical)

    • TRUE に設定すると、解 X に加えて、解の共分散行列や行列のランクなどの詳細な情報が返されます。type = 1 の場合のみ有効です。
  • verbose: (logical)

    • TRUE (デフォルト) に設定すると、計算中に警告メッセージなどが表示されます。
  • lower, upper: (vector or NULL)

    • 未知数 x の各要素に対する単純な下限・上限 (x_i >= lower_i, x_i <= upper_i) を指定するための簡易的な引数です。内部的にこれらは不等式制約 Gx >= H の形式に変換されます。例えば、lower = 0 は、全ての x の要素が非負であるという制約 x_i >= 0 を課します。

シミュレーション

ここでは、lsei関数を確認するために、あるメーカーの生産計画問題を想定したシミュレーションを行います。

シナリオ設定

3つの製品（製品1, 製品2, 製品3）を生産する工場を考えます。目的は、複数の制約を満たしつつ、各製品の生産量を市場の需要予測に最も近づけることです。

  • 未知数 x:

    • x1, x2, x3 (それぞれ製品1, 2, 3の生産量)
  • 目的 (最小二乗 Ax ≈ B):

    • 生産量を市場の需要予測 (80, 90, 120) に可能な限り近づけたい。
    • || I * x - B ||^2 を最小化します。ここで I は単位行列です。
  • 等式制約 (Ex = F):

    • 全製品の生産に必要な総労働時間は、厳密に400時間でなければならない。
    • 各製品の生産に要する時間は (2, 3, 2.5) 時間/個とします。
    • 2*x1 + 3*x2 + 2.5*x3 = 400
  • 不等式制約 (Gx >= H):

    1. 全ての製品の生産量は0以上でなければならない (x_i >= 0)。
    2. 原材料Aの総使用量は、在庫の250単位を超えてはならない。
      • 各製品の生産に必要な原材料Aは (1, 2, 2) 単位/個とします。
      • 1*x1 + 2*x2 + 2*x3 <= 250 (これは -1*x1 - 2*x2 - 2*x3 >= -250 と変形します)
    3. 製品3は、その特殊性から最低でも20個は生産する必要がある (x3 >= 20)。

Rコードによるシミュレーション

以下に、上記シナリオをlsei関数で解くためのRコードを示します。

# 1. 問題設定: 行列とベクトルの作成

# 目的: 生産量を需要予測に近づける (Ax ≈ B)
# Aは単位行列、xは生産量ベクトル(x1, x2, x3)
A <- diag(3)
# Bは需要予測ベクトル
B <- c(80, 90, 120)
colnames(A) <- c("製品1", "製品2", "製品3")

# 等式制約: 総労働時間を厳密に400時間とする (Ex = F)
# Eは各製品の労働時間係数
E <- matrix(c(2, 3, 2.5), nrow = 1)
# Fは総労働時間
F <- 400

# 不等式制約: 生産上の制約を満たす (Gx >= H)
G <- rbind(
  diag(3), # 制約1: 全ての生産量は0以上 (x_i >= 0)
  c(-1, -2, -2), # 制約2: 原材料Aの使用量は250以下
  c(0, 0, 1) # 制約3: 製品3は20以上
)
H <- c(
  0, 0, 0, # 制約1の右辺
  -250, # 制約2の右辺
  20 # 制約3の右辺
)

# 2. lsei関数による最適化計算の実行
result <- lsei(A = A, B = B, E = E, F = F, G = G, H = H)

# 3. 結果の表示と解釈
cat("--- 計算結果の概要 ---\n")
cat("解の妥当性 (IsError):", result$IsError, "\n")
# IsErrorがFALSEであれば、実行可能な解が見つかったことを意味します。

cat("\n--- 最適生産量 (ベクトルX) ---\n")
print(round(result$X, 2))

cat("\n--- 目的関数の評価 ---\n")
# solutionNormは ||Ax - B||^2 の値です。
# この値が小さいほど、解が需要予測に近いことを示します。
cat("需要予測との誤差二乗和 (Solution Norm):", result$solutionNorm, "\n")
--- 計算結果の概要 ---
解の妥当性 (IsError): FALSE 

--- 最適生産量 (ベクトルX) ---
製品1 製品2 製品3 
88.82 41.76 38.82 

--- 目的関数の評価 ---
需要予測との誤差二乗和 (Solution Norm): 8994.118 
cat("--- 制約条件の検証 ---\n")
# 等式制約の検証 (Ex - F)
equality_check <- E %*% result$X - F
cat("等式制約 (総労働時間) の残差:", equality_check, "\n")
# この値が0に近い場合、等式制約は満たされています。
--- 制約条件の検証 ---
等式制約 (総労働時間) の残差: 1.136868e-13

lsei関数によって算出された解が、設定された等式制約、すなわち「総労働時間を厳密に400時間とする」という条件をどの程度正確に満たしているかを検証したものです。

なお、ここで「残差」とは、等式制約の左辺（E %*% X、解から計算された実際の総労働時間）と右辺（F、目標値である400）の間の差を指します。

もし制約が完全に満たされていれば、この残差は0になり、結果は1.136868 × 10⁻¹³と極めて0に近い数値ですので、最適化計算は制約条件を遵守したと言えます。

# 不等式制約の検証 (Gx - H)
inequality_check <- G %*% result$X - H
cat("不等式制約の残差 (全て非負であるべき):\n")
print(round(inequality_check, 5))
# これらの値が全て0以上であれば、不等式制約は満たされています。
不等式制約の残差 (全て非負であるべき):
         [,1]
[1,] 88.82353
[2,] 41.76471
[3,] 38.82353
[4,]  0.00000
[5,] 18.82353

lsei関数によって算出された解が、設定された5つの不等式制約（Gx >= H）を全て満たしているかどうかの検証結果を示しています。

各行の数値は、不等式制約の左辺（G %*% X）から右辺（H）を引いた値、すなわち「残差」または「余剰」を表します。

不等式制約が満たされている場合、これらの値は全て0以上になる必要があります。

  1. [1,] 88.82353:

    • これは第1の制約 x1 >= 0 に対する結果です。生産量 x1 は 88.82353 であり、制約は満たされています。
  2. [2,] 41.76471:

    • これは第2の制約 x2 >= 0 に対する結果です。生産量 x2 は 41.76471 であり、制約は満たされています。
  3. [3,] 38.82353:

    • これは第3の制約 x3 >= 0 に対する結果です。生産量 x3 は 38.82353 であり、制約は満たされています。
  4. [4,] 0.00000:

    • これは第4の制約 x1 + 2*x2 + 2*x3 <= 250(-1*x1 - 2*x2 - 2*x3 >= -250)（原材料Aの使用量）に対する結果です。残差が0であるということは、この制約が上限ぎりぎりまで使われていることを意味します。つまり、原材料Aの総使用量が、在庫の上限である250単位に完全に達している状態であり、この最適化問題における生産量のボトルネック（制限要因）の一つであることを示唆しています。
  5. [5,] 18.82353:

    • これは第5の制約 x3 >= 20（製品3の最低生産量）に対する結果です。実際の生産量 x3（38.82353個）が、最低ラインである20個を 18.82353 個上回っていることを示します。それゆえ、この制約も満たされています。

表示された全ての数値が0以上であることから、算出された最適解は、設定された全ての不等式制約を正しく遵守していることが確認できます。

# 4. 結果の可視化
# ベクトルの名前を設定
solution_x <- result$X
names(solution_x) <- colnames(A)

# 棒グラフの戻り値(棒グラフのx座標)を保存
bar_coords <- barplot(
  height = solution_x,
  main = "最適生産計画",
  xlab = "製品",
  ylab = "生産量 (個)",
  col = "skyblue",
  ylim = c(0, max(solution_x, B) * 1.2)
)

# 保存したx座標を使用して点をプロット
points(
  x = bar_coords,
  y = B,
  pch = 4,
  col = "red",
  cex = 2,
  lwd = 2
)

legend(
  "topright",
  legend = c("最適生産量", "需要予測"),
  fill = c("skyblue", NA),
  border = c("black", NA),
  pch = c(NA, 4),
  col = c(NA, "red"),
  bty = "n"
)
Figure 1

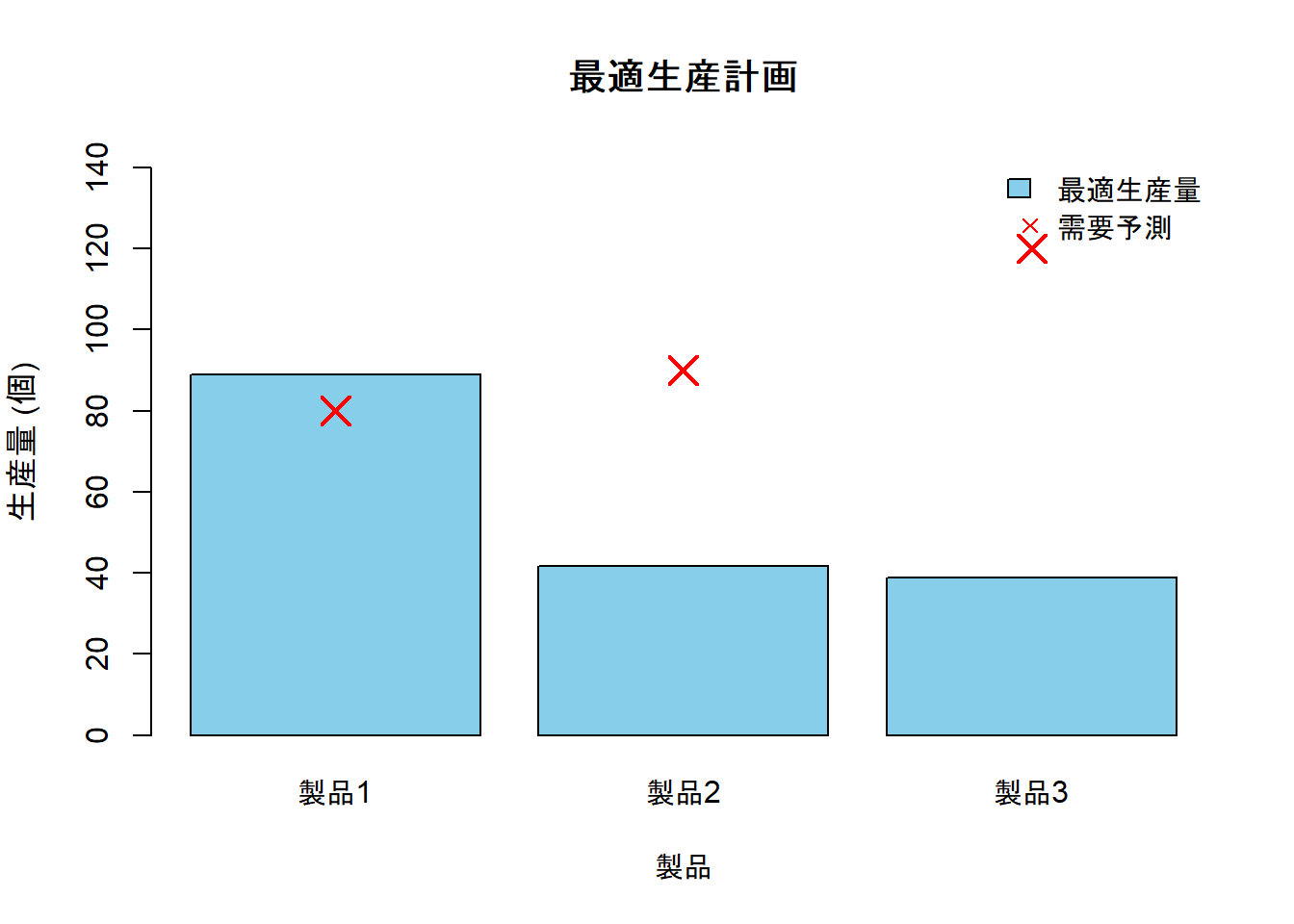
Figure 1 は、lsei関数によって算出された制約条件下での最適な各製品の生産量を示しており、理想（需要予測）と現実（制約下での最適解）の間の関係を視覚的に明らかにしています。

  • 棒グラフ (最適生産量): 「製品1」「製品2」「製品3」それぞれの最適生産量を表します。この生産量は、総労働時間、原材料の在庫、最低生産義務といった、設定された全ての制約条件を厳密に満たした上で、全体の目標（需要予測）との誤差を最小化する生産計画です。
  • 赤色の×印 (需要予測): 各棒の上または近くにプロットされた赤色の×印は、制約を考慮する前の設定した市場の需要予測を示しています。これは、生産計画における理想的な目標と設定した値です。
  • 製品1の生産量は、需要予測（80個）をわずかに上回っています。
  • 一方で、製品2および製品3の生産量は、それぞれの需要予測（90個、120個）を大幅に下回っています。

この結果は、与えられた制約（「総労働時間は厳密に400時間」「原材料Aの使用量は250単位以下」等）の下、需要が高いにも関わらず製品2と製品3の生産量を犠牲にして、製品1を需要より多く生産する生産計画が、制約条件全体を満たしながら目的関数 ||Ax - B||^2 を最小化できる、つまり需要予測との誤差が最も小さくなる生産計画であることを示唆しています。

以上です。