Rの関数:plsr {pls}

モデルの基本情報

Data:   X dimension: 100 10 
    Y dimension: 100 1
Fit method: kernelpls
Number of components considered: 10

• Data: モデルに使用されたデータの次元を示しています。
  • X dimension: 100 10 は、説明変数が10個、サンプルサイズが100であることを意味します。
  • Y dimension: 100 1 は、目的変数が1個、サンプルサイズが100であることを意味します。
• Fit method: kernelpls: モデルの計算に使用されたアルゴリズムがkernelplsであることを示しています。
• Number of components considered: 10: モデルを評価するために考慮された潜在変数（成分）の最大数が10であることを示しています。

モデルの予測性能評価 (VALIDATION: RMSEP)

VALIDATION: RMSEP
Cross-validated using 10 random segments.
       (Intercept)  1 comps  2 comps  3 comps  4 comps  5 comps  6 comps  7 comps  8 comps  9 comps  10 comps
CV           1.579   0.7590   0.6699   0.4865   0.4796   0.4815   0.4823   0.4824   0.4824   0.4824    0.4824
adjCV        1.579   0.7522   0.6761   0.4842   0.4767   0.4785   0.4792   0.4793   0.4793   0.4793    0.4793

このセクションは、モデルの予測性能を示しています。

• Cross-validated using 10 random segments.: 予測性能の評価が、データを10個のグループにランダムに分割して行う「10-fold クロスバリデーション」によって行われたことを示します。この手法により、未知のデータに対するモデルの予測精度（汎化性能）をより客観的に評価できます。
• RMSEP (Root Mean Squared Error of Prediction): 予測誤差の平方根平均を表す指標です。この値が小さいほど、モデルの予測精度が高いことを意味します。
  • CV: クロスバリデーションによって計算されたRMSEPの値です。
  • adjCV: 自由度で調整された、より不偏なRMSEPの値です。
• 結果の解釈:
  • (Intercept)は成分を一つも使わない場合（つまり、目的変数の平均値で予測した場合）の誤差で、1.579です。
  • 成分数を1から順に増やしていくと、adjCVの値は 0.7522, 0.6761, 0.4842 と減少し、4成分（4 comps）の時に最小値0.4767を記録します。
  • 5成分以降は、adjCVの値がわずかに増加またはほぼ横ばいになっています。
  • 結論: この結果は、4つの成分を持つモデルが、予測精度とモデルの簡潔さのバランスが最も良いことを示唆しています。それゆえ、このモデルを採用する際の最適な成分数は4であると判断できます。

訓練データへの適合度 (TRAINING: % variance explained)

TRAINING: % variance explained
   1 comps  2 comps  3 comps  4 comps  5 comps  6 comps  7 comps  8 comps  9 comps  10 comps
X    26.77    77.02    81.92    84.73    87.42    89.85    92.16    94.83    97.37    100.00
Y    78.53    82.57    91.83    92.56    92.60    92.61    92.61    92.61    92.61     92.61

このセクションは、構築したモデルが、訓練に使用したデータそのものをどの程度うまく説明できているか（適合度）を示しています。

• % variance explained: 各成分数を採用したモデルが、データ全体のばらつき（分散）を何パーセント説明できているかを示します。
• X: 説明変数（X）の分散のうち、モデルによって説明される割合です。成分数を増やすほど、説明変数の情報をより多く取り込むため、この値は単調に増加し、最終的に100%になります。
• Y: 目的変数（Y）の分散のうち、モデルによって説明される割合です。通常の回帰分析における決定係数（R-squared）に相当する指標です。
• 結果の解釈:
  • Yの行を見ると、1成分だけで目的変数の分散の78.53%を説明できています。
  • 成分数を3から4に増やすと、分散説明率は91.83%から92.56%へと上昇しますが、5成分以降はほとんど増加していません (92.60%, 92.61%…)。
  • この結果もまた、4成分を超えてモデルを複雑にしても、目的変数を説明する能力はほとんど向上しないことを示しています。

総合的な結論

以上のsummary()の結果を総合的に判断すると、以下のようになります。

クロスバリデーションによる予測性能（RMSEP）は4成分で最も優れており、また、目的変数の分散説明率も4成分以降は頭打ちになっています。それゆえ、このデータに対するPLS回帰モデルとしては、4つの成分を採用することが最も妥当であると結論付けられます。

RMSEPプロットによる最適な成分数の決定

# モデルの評価を行い、結果を可視化します。

# クロスバリデーションによる予測誤差(RMSEP)をプロットし、モデルの複雑さ（成分数）と予測精度のバランスを評価します。
cat("--- 最適な成分数の検討 ---\n")
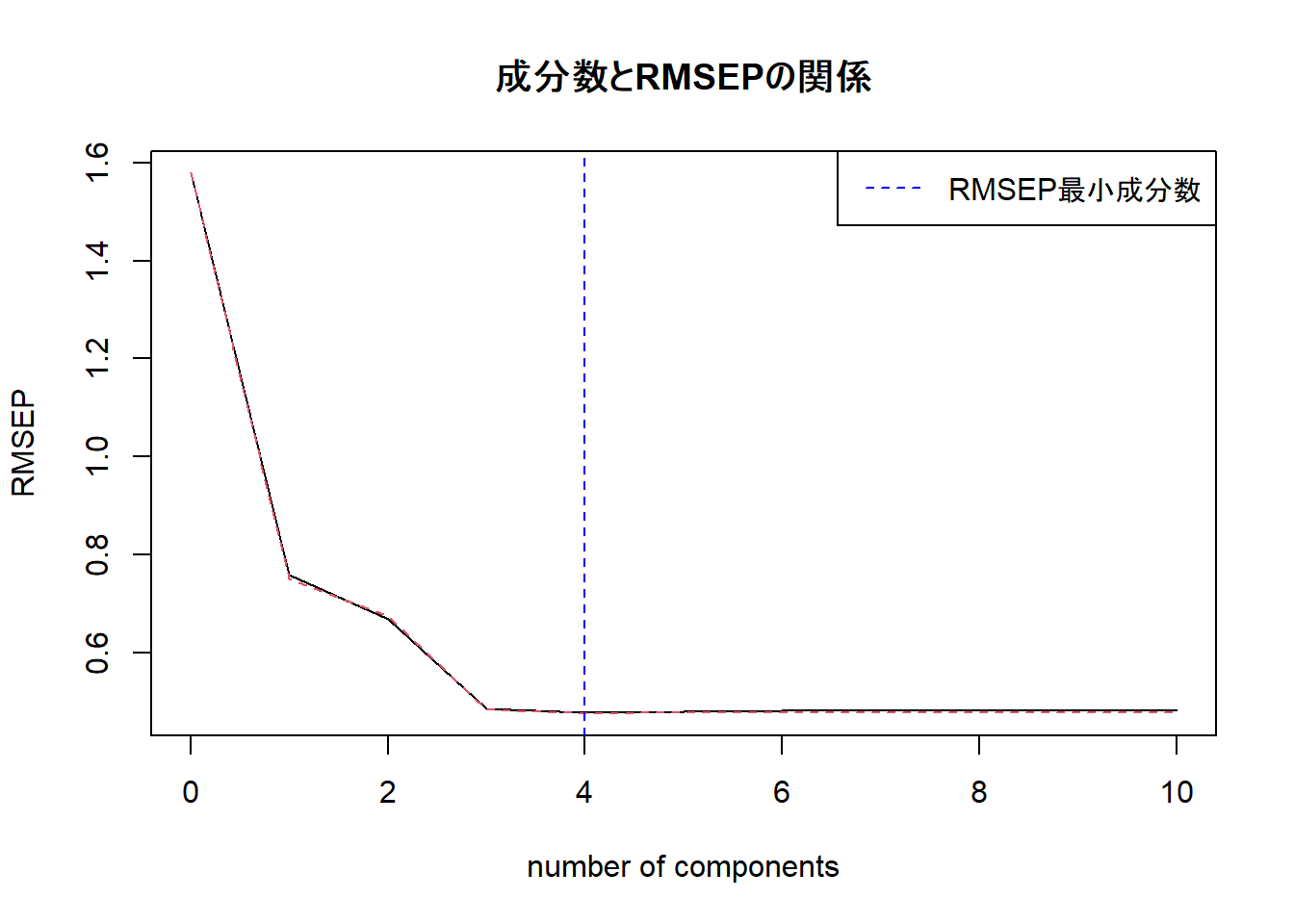
validationplot(pls_model, val.type = "RMSEP", main = "成分数とRMSEPの関係")
optimal_ncomp <- which.min(RMSEP(pls_model)$val[1, 1, -1])
cat(paste("RMSEPが最小となる成分数:", optimal_ncomp, "\n\n"))
abline(v = optimal_ncomp, col = "blue", lty = 2)
legend("topright", legend = "RMSEP最小成分数", col = "blue", lty = 2)

--- 最適な成分数の検討 ---
RMSEPが最小となる成分数: 4 

RMSEPが最も小さくなる点が最適な成分数の一つの目安です。

Figure 1 から、成分数が4あたりでRMSEPが最小になり、その後はほぼ横ばいになることが見て取れます。それゆえ、このモデルでは4成分を採用するのが妥当であると判断できます。

予測値と実測値の比較プロット

# 構築したモデル（成分数4）がどの程度データを説明できているかを確認するため、
# 予測値と実測値をプロットします。
plot(pls_model,
  ncomp = optimal_ncomp, asp = 1, line = TRUE,
  main = paste("予測値 vs 実測値 (成分数 = ", optimal_ncomp, ")", sep = ""),
  xlab = "実測値", ylab = "クロスバリデーションによる予測値"
)

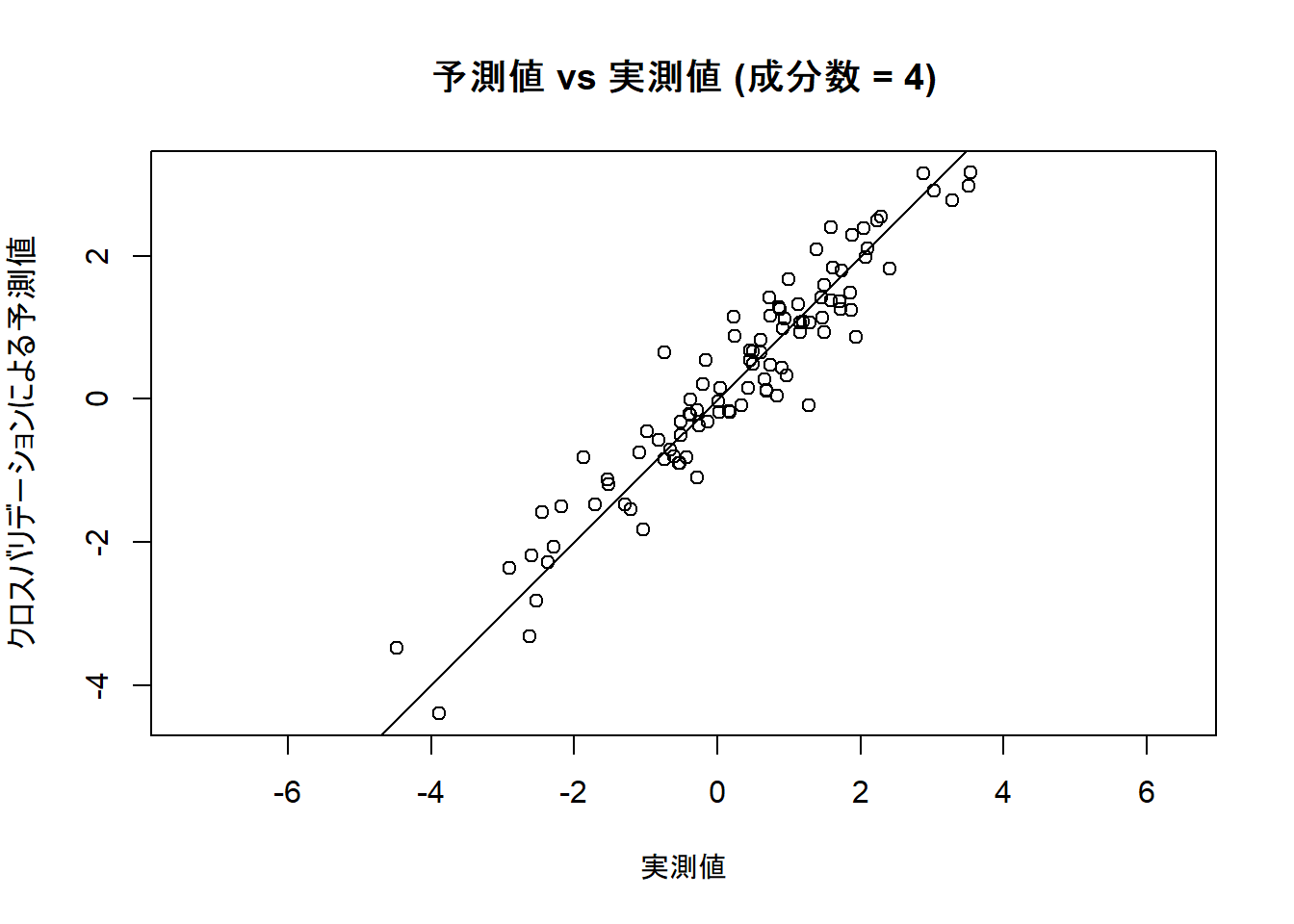
Figure 2 の各軸等と傾向等は以下のとおりです。

• 横軸 (X軸): 「実測値」
  • サンプルデータに含まれる、実際の目的変数Yの値です。
• 縦軸 (Y軸): 「クロスバリデーションによる予測値」
  • モデルがクロスバリデーションの過程で予測したYの値です。訓練データそのものではなく、未知のデータに対する予測値を模しているため、モデルの汎化性能をより反映します。
• 各点 (プロットされた円):
  • データセット内の100個のサンプルそれぞれに対応します。各点のX座標がそのサンプルの「実測値」、Y座標が「予測値」です。
• 対角線 (y = x の直線):
  • 予測値と実測値が完全に一致する「理想的な予測」の状態を示す基準線です。
• 全体的な傾向:
  • プロットされた点は、全体として右肩上がりの対角線に沿って分布しています。これは、実測値が大きいサンプルに対しては予測値も大きく、実測値が小さいサンプルに対しては予測値も小さくなるという、モデルがデータの傾向を捉えられていることを示しています。
• 予測精度:
  • 多くの点が対角線の近くに位置しています。これは、モデルの予測値と実測値の差（予測誤差）が小さいことを意味します。
  • もしモデルの精度が低ければ、点は対角線から大きくばらついて分布するはずです。このプロットのように点が対角線周辺に密集している状態は、モデルが高い予測精度を持つことの視覚的示唆となります。

以下に、Figure 2 の各点の数値を抽出するコードを記します。

# x座標（実測値）を元のデータフレームから取得します。
jissokuchi <- sim_data$Y

# y座標（クロスバリデーションによる予測値）をモデルオブジェクトから取得します。
# pls_model$validation$pred は [サンプル, 目的変数, 成分数] の3次元配列になっています。
# 今回は、目的変数は1つ目、成分数は optimal_ncomp (4) を指定します。
yosokuchi_cv <- pls_model$validation$pred[, 1, optimal_ncomp]

# 抽出した値をデータフレームにまとめます。
plot_data <- data.frame(
  Jissokuchi = jissokuchi,
  Yosokuchi_CV = yosokuchi_cv
)

# 抽出したデータの一部を確認します。
cat("--- 抽出したプロット上の座標データの一部を確認 ---\n")
print(str(plot_data))

--- 抽出したプロット上の座標データの一部を確認 ---
'data.frame':   100 obs. of  2 variables:
 $ Jissokuchi  : num  0.994 1.858 0.909 -1.517 -1.037 ...
 $ Yosokuchi_CV: num  1.67 1.48 0.98 -1.2 -1.83 ...
NULL

回帰係数のプロット

# 各説明変数がモデルにどの程度寄与しているか、回帰係数を可視化します。
plot(pls_model, "coefficients",
  ncomp = optimal_ncomp,
  main = paste("回帰係数 (成分数 = ", optimal_ncomp, ")", sep = ""),
  xlab = "説明変数", ylab = "係数の値"
)

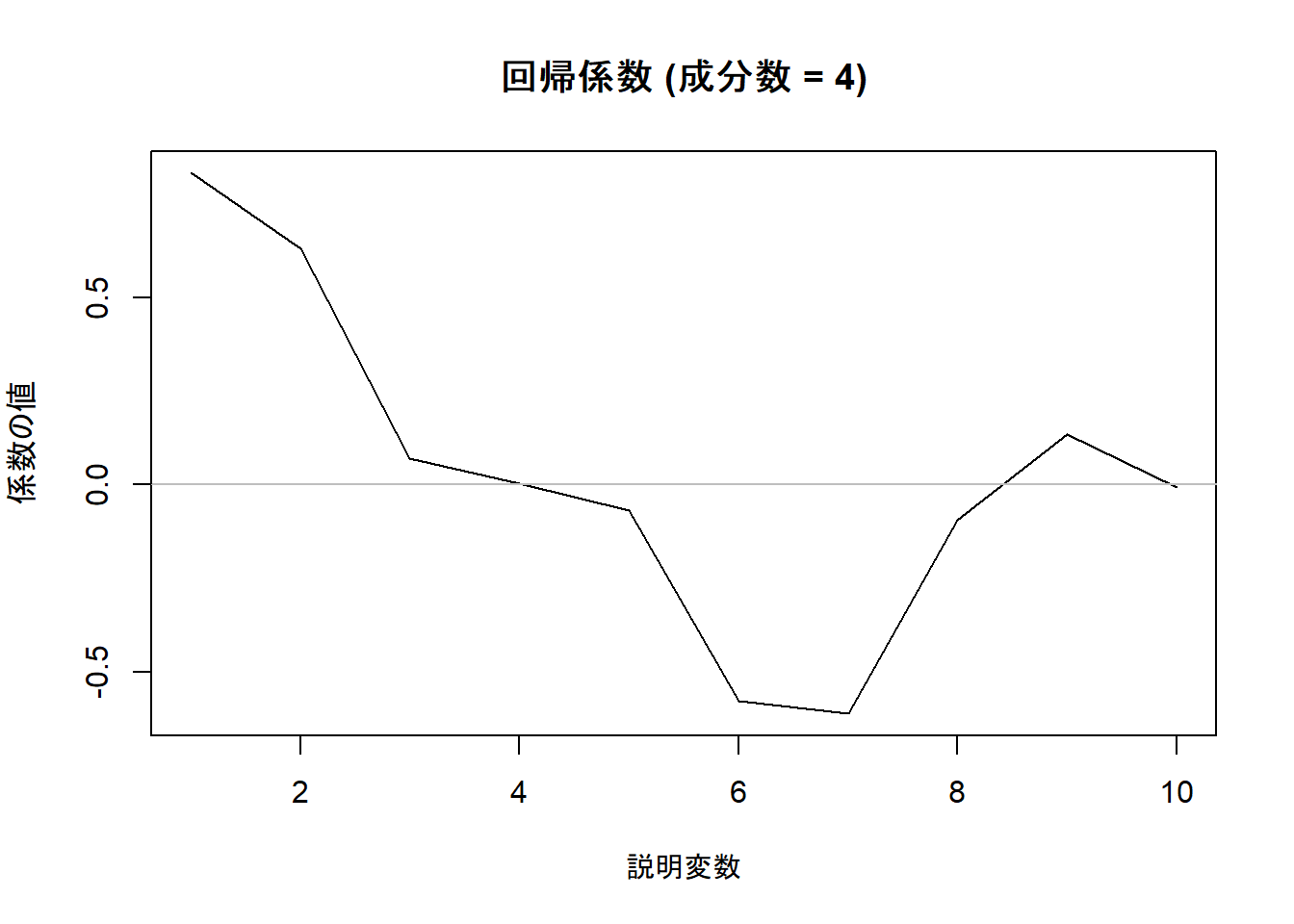
成分数 4 のモデルにおける各説明変数の回帰係数を Figure 3 としてプロットしました。

Yの生成式で大きな係数を設定した変数（X1, X2, X6, X7）が、実際に大きな（絶対値の）係数を持っていることが確認できます。

以下に、成分数を4とした場合の各説明変数の回帰係数を抽出するコードを記します。

pls_model$coefficients[, 1, optimal_ncomp]

          X1           X2           X3           X4           X5           X6           X7           X8           X9          X10 
 0.833860748  0.632518814  0.071485190  0.003309335 -0.067332312 -0.578370869 -0.611732460 -0.093559939  0.134858130 -0.007454024 

以上です。