Rの関数から gwr {spgwr} を確認します。
関数 gwr とは
gwr (Geographically Weighted Regression:地理的加重回帰) は、回帰係数が空間的に一定であると仮定する通常の回帰分析(OLS)とは異なり、場所(座標)ごとに異なる回帰係数を推定するための関数です。
「ある地点の現象は、遠くの地点よりも近くの地点の影響を強く受ける」という 地理学の第一法則 に基づき、推定したい地点の近傍にあるデータに対して、距離に応じた重み(Kernel Weight)を与えて局所的に回帰分析を行います。
これにより、変数間の関係性が地域によってどのように変化するか(空間的異質性)を明らかにできます。
関数 gwr の引数
library(spgwr)
args(gwr)function (formula, data = list(), coords, bandwidth, gweight = gwr.Gauss,
adapt = NULL, hatmatrix = FALSE, fit.points, longlat = NULL,
se.fit = FALSE, weights, cl = NULL, predictions = FALSE,
fittedGWRobject = NULL, se.fit.CCT = TRUE)
NULL- formula
- 回帰モデルの構造を指定する式(例:
y ~ x1 + x2)。 - 従属変数と説明変数の関係を定義します。
- 回帰モデルの構造を指定する式(例:
- data
-
formulaで使用する変数を含むデータフレーム。 - 分析対象のデータセットを提供します。
-
- coords
- 各観測地点の座標行列(2列の行列またはデータフレーム)。
- データの空間的な位置を指定します。
dataが通常のデータフレームの場合、必須となります。列名は通常 x, y(または経度, 緯度)です。
- bandwidth
- バンド幅(帯域幅)。
- 重み付け関数の「広がり」を決定するパラメータです。固定カーネルの場合は距離、適応型カーネルの場合は近傍点の数などを意味します。
- gweight
- 重み付けに使用するカーネル関数。デフォルトは
gwr.Gauss(ガウシアンカーネル)。 - 距離に応じて重みがどのように減衰するかを定義します。
- 重み付けに使用するカーネル関数。デフォルトは
- adapt
- 適応型バンド幅を使用する場合の、近傍点の割合(0 ~ 1 の数値)。
- データ密度が不均一な場合に有用です。例えば
0.1を指定すると、各地点で最も近い 10% のデータが含まれるようにバンド幅が地点ごとに自動調整されます。
- hatmatrix
- ハット行列(射影行列)を計算するかどうかの論理値。
- GWRモデルの診断統計量(AICcなど)や標準誤差を計算するために必要です。
- fit.points
- 回帰係数を推定する地点の座標。
- デフォルトでは観測地点(
coords)と同じ場所で推定を行いますが、メッシュグリッド上など、データがない地点での係数を予測したい場合に指定します。
- longlat
- 座標が経度・緯度であるかを示す論理値。
-
TRUEの場合、ユークリッド距離ではなく大圏距離(地球上の曲面距離)を用いて距離計算を行います。
- se.fit
- 推定された係数の標準誤差を計算するかどうかの論理値。
- 係数の信頼性を評価するために使用します。
hatmatrix = TRUEの場合は自動的にTRUEになります。
- weights
- 観測値ごとの重み(数値ベクトル)。
- 地理的な重みとは別に、データ自体の信頼性や重要度に差がある場合(加重最小二乗法的な意味合い)に使用します。
- cl
- 並列計算用のクラスタオブジェクト。
- 計算時間を短縮するために、マルチコアでの並列処理を行う場合に指定します。
- predictions
- 従属変数の予測値を計算して返すかどうかの論理値。
- モデルの当てはまりを確認する際に使用します。
fit.pointsが指定されている場合は、その地点での予測値となります。
- fittedGWRobject
- 既に適合済みのGWRオブジェクト。
- 計算の重複を避けるため、既存の結果を利用して予測のみを行う場合などに使用されます。
- se.fit.CCT
- 標準誤差計算時の補正方法に関する論理値。
- 内部的な計算手法の選択肢であり、通常はデフォルト(
TRUE)を使用します。
シミュレーション用サンプルデータとコード
gwr 関数の特性(場所によって係数が変わる)を確認するため、以下の手順でサンプルデータを作成し、シミュレーションを行います。
- 空間構造の生成:
- \(20 \times 20\) のグリッド座標を作成します。
- 真のパラメータ設定:
- 回帰係数 \(\beta\) を定数ではなく、座標 \((u, v)\) の関数として定義します。
- \(\beta_1\): 東へ行くほど大きくなる(空間的勾配)。
- \(\beta_2\): 北へ行くほど小さくなる、あるいは波打つような変動。
- データ生成:
- \(y_i = \beta_{0} + \beta_{1, i} x_{1, i} + \beta_{2, i} x_{2, i} + \epsilon_i\) の式で従属変数を生成します。
- 比較検証:
- 通常の線形回帰(OLS)ではこの構造を捉えきれないが、GWRでは係数の空間分布を復元できることを確認します。
以下はRコードです。
空間構造とサンプルデータの作成
# 必要なパッケージの読み込み
library(ggplot2)
library(gridExtra)
library(viridis)
# 乱数シードの固定
seed <- 20251204
set.seed(seed)
# グリッドサイズの設定(20x20 = 400地点)
side_length <- 20
n <- side_length * side_length
# 座標データの作成
coords <- expand.grid(x = 1:side_length, y = 1:side_length)
# data.frame形式の座標(gwr関数のcoords引数用)
coords_mat <- as.matrix(coords)
# 説明変数 X1, X2 の生成(一様乱数と正規乱数)
X1 <- runif(n, 10, 20)
X2 <- rnorm(n, 5, 1)真の係数を空間座標の関数として定義
# beta_0 (切片): 定数とする
beta_0_true <- 10
# beta_1: X座標に依存して線形に増加する (西:小さい -> 東:大きい)
# 例: 1.0 から 3.0 まで変化
beta_1_true <- 1.0 + (coords$x / side_length) * 2.0
# beta_2: Y座標に依存して変化する (南:大きい -> 北:小さい)
# 例: 0.5 から -1.5 まで変化
beta_2_true <- 0.5 - (coords$y / side_length) * 2.0従属変数 y の生成 (局所的な係数に基づくデータ生成)
# 誤差項
epsilon <- rnorm(n, mean = 0, sd = 1.0)
# 真のモデル: y = beta0 + beta1(u,v)*X1 + beta2(u,v)*X2 + error
y <- beta_0_true + beta_1_true * X1 + beta_2_true * X2 + epsilon
# 分析用データフレームの作成
sim_data <- data.frame(
y = y,
x1 = X1,
x2 = X2,
coord_x = coords$x,
coord_y = coords$y
)
cat("--- 作成したサンプルデータの一部を確認 ---\n")
print(str(sim_data))--- 作成したサンプルデータの一部を確認 ---
'data.frame': 400 obs. of 5 variables:
$ y : num 27.1 26.1 36.3 40.4 29.2 ...
$ x1 : num 13.3 11.1 17.3 19.7 10.6 ...
$ x2 : num 4.63 5.79 5.68 5.23 6.08 ...
$ coord_x: int 1 2 3 4 5 6 7 8 9 10 ...
$ coord_y: int 1 1 1 1 1 1 1 1 1 1 ...
NULL真の係数分布の可視化 (確認用)
plot_data <- cbind(sim_data, b1 = beta_1_true, b2 = beta_2_true)
p_true1 <- ggplot(plot_data, aes(x = coord_x, y = coord_y, fill = b1)) +
geom_tile() +
scale_fill_viridis(option = "plasma") +
labs(title = "真の係数 beta_1 の分布", x = "X座標", y = "Y座標", fill = "値") +
theme_minimal()
p_true2 <- ggplot(plot_data, aes(x = coord_x, y = coord_y, fill = b2)) +
geom_tile() +
scale_fill_viridis(option = "viridis") +
labs(title = "真の係数 beta_2 の分布", x = "X座標", y = "Y座標", fill = "値") +
theme_minimal()モデルの推定と比較
バンド幅は、bandwidth(固定距離)か adapt(近傍割合)を指定する必要があります。ここでは gwr.sel(..., adapt = TRUE) を用いて、AICcを最小化する最適な近傍点数の割合(適応型バンド幅)を探索します。
さらに、関数gwrの引数を、adapt = bw_optimal として、空間的な重みの広がりを指定し、hatmatrix = TRUE を指定してAICcを計算します。
# (A) 通常の線形回帰 (OLS) - 係数は全域で一定と仮定
model_ols <- lm(y ~ x1 + x2, data = sim_data)
cat("--- (A) 通常の線形回帰 (OLS) - 係数は全域で一定と仮定 ---\n")
summary(model_ols)
# (B) 地理的加重回帰 (GWR)
# まず、gwr.sel関数を利用して、最適なバンド幅を計算します。
bw_optimal <- gwr.sel(y ~ x1 + x2, data = sim_data, coords = coords_mat, adapt = TRUE, verbose = FALSE)
# gwr関数の実行
# adapt引数に最適化された割合を渡します。hatmatrix=TRUEで診断統計量を計算させます。
model_gwr <- gwr(
formula = y ~ x1 + x2,
data = sim_data,
coords = coords_mat,
adapt = bw_optimal, # 最適化された適応型バンド幅
hatmatrix = TRUE, # AICcなどを計算するために必要
se.fit = TRUE # 標準誤差を計算
)
cat("--- (B) 地理的加重回帰 (GWR) ---\n")
model_gwr--- (A) 通常の線形回帰 (OLS) - 係数は全域で一定と仮定 ---
Call:
lm(formula = y ~ x1 + x2, data = sim_data)
Residuals:
Min 1Q Median 3Q Max
-20.9826 -7.0975 0.0929 7.1165 22.6048
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 9.5097 3.2646 2.913 0.00378 **
x1 2.2104 0.1622 13.624 < 2e-16 ***
x2 -0.9269 0.4412 -2.101 0.03627 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 9.087 on 397 degrees of freedom
Multiple R-squared: 0.3216, Adjusted R-squared: 0.3181
F-statistic: 94.09 on 2 and 397 DF, p-value: < 2.2e-16
--- (B) 地理的加重回帰 (GWR) ---
Call:
gwr(formula = y ~ x1 + x2, data = sim_data, coords = coords_mat,
adapt = bw_optimal, hatmatrix = TRUE, se.fit = TRUE)
Kernel function: gwr.Gauss
Adaptive quantile: 0.003969022 (about 1 of 400 data points)
Summary of GWR coefficient estimates at data points:
Min. 1st Qu. Median 3rd Qu. Max. Global
X.Intercept. -3.098401 6.301054 9.100877 11.928214 21.235850 9.5097
x1 0.770815 1.543944 2.062398 2.611193 3.496472 2.2104
x2 -3.265040 -1.059615 -0.440959 0.086308 1.393395 -0.9269
Number of data points: 400
Effective number of parameters (residual: 2traceS - traceS'S): 215.7545
Effective degrees of freedom (residual: 2traceS - traceS'S): 184.2455
Sigma (residual: 2traceS - traceS'S): 1.051328
Effective number of parameters (model: traceS): 160.7382
Effective degrees of freedom (model: traceS): 239.2618
Sigma (model: traceS): 0.9225712
Sigma (ML): 0.7135207
AICc (GWR p. 61, eq 2.33; p. 96, eq. 4.21): 1410.465
AIC (GWR p. 96, eq. 4.22): 1025.854
Residual sum of squares: 203.6447
Quasi-global R2: 0.9957854 通常の最小二乗法 (OLS) の結果
Coefficients:
Estimate ...
(Intercept) 9.5097 ...
x1 2.2104 ...
x2 -0.9269 ...
Multiple R-squared: 0.3216
Residual standard error: 9.087- 係数 (Coefficients):
- x1: 推定値
2.21。真の値は場所によって \(1.0 \sim 3.0\) と変化しますが、OLSはその平均的な値として約 \(2.2\) を推定しています。 - x2: 推定値
-0.93。真の値は \(0.5 \sim -1.5\) と変化しますが、こちらもその中間的な値を推定しています。 - これらは「空間的な平均」としては間違っていませんが、個々の地点での関係性を正しく表してはいません。
- x1: 推定値
- モデルの当てはまり:
- R-squared (決定係数):
0.3216。変動の約32%しか説明できておらず、「係数を定数と仮定するモデル(OLS)が不適切である」ことを示唆しています。 - Residual standard error (残差標準誤差):
9.087。予測と実測のズレが大きく、モデルがデータの変動を捉えきれていないことを意味します。
- R-squared (決定係数):
地理的加重回帰 (GWR) の結果
Adaptive quantile: 0.003969022 (about 1 of 400 data points)
Summary of GWR coefficient estimates at data points:
Min. 1st Qu. Median 3rd Qu. Max. Global
X.Intercept. -3.098401 6.301054 9.100877 11.928214 21.235850 9.5097
x1 0.770815 1.543944 2.062398 2.611193 3.496472 2.2104
x2 -3.265040 -1.059615 -0.440959 0.086308 1.393395 -0.9269
Sigma (residual: ...): 1.051328
Quasi-global R2: 0.9957854 - バンド幅 (Adaptive quantile):
-
0.0039...と小さい値が選ばれました。これは各地点の回帰において、ごく近傍のデータ(約1点+周辺の重み)を強く参照していることを意味します。シミュレーションデータが滑らかかつ明確な勾配を持っているため、局所的な適合度を高める設定が選ばれました。
-
- 係数の分布 (Summary of GWR coefficient estimates):
- Global列はOLSの推定値と一致します。確認する点は Min. (最小値) から Max. (最大値) の範囲です。
- x1: 範囲
0.77~3.50。- 真の値の範囲(\(1.0 \sim 3.0\))をカバーしており、場所によって係数が大きく変動していることを捉えています。
- x2: 範囲
-3.27~1.39。- 真の値の範囲(\(-1.5 \sim 0.5\))の傾向(負の値から正の値まで)を捉えています。端点の影響(エッジ効果)やノイズにより範囲が少し広くなっていますが、構造は復元されています。
- モデルの当てはまり:
- Sigma (residual):
1.05。OLSの9.09から減少しました。誤差項の標準偏差(設定値は1.0)に近く、ノイズ以外の構造をほぼ説明できていることを意味します。 - Quasi-global R2:
0.9958。OLS(32%)と異なり、変動の約99.6%を説明できています。
- Sigma (residual):
結果の可視化
# GWRの結果から推定された係数を取り出す
# model_gwr$SDF は SpatialPointsDataFrame ですが、as.data.frame()を使うと
# 通常は属性データ(係数など)のみが取り出され、座標は含まれません。
results_df <- as.data.frame(model_gwr$SDF)
# プロット用に座標列をデータフレームに追加します
results_df$coord_x <- sim_data$coord_x
results_df$coord_y <- sim_data$coord_y
# OLSの結果(定数)
ols_coef <- coef(model_ols)
# 推定された係数の可視化
# results_df には説明変数の名前(x1, x2)で「ローカルな係数値」が格納されています
# beta_1 の推定結果
p_est1 <- ggplot(results_df, aes(x = coord_x, y = coord_y, fill = x1)) +
geom_tile() +
scale_fill_viridis(option = "plasma") +
labs(
title = "GWR推定係数 beta_1 の分布",
subtitle = paste("OLS推定値:", round(ols_coef["x1"], 3)),
x = "X座標", y = "Y座標", fill = "係数値"
) +
theme_minimal()
# beta_2 の推定結果
p_est2 <- ggplot(results_df, aes(x = coord_x, y = coord_y, fill = x2)) +
geom_tile() +
scale_fill_viridis(option = "viridis") +
labs(
title = "GWR推定係数 beta_2 の分布",
subtitle = paste("OLS推定値:", round(ols_coef["x2"], 3)),
x = "X座標", y = "Y座標", fill = "係数値"
) +
theme_minimal()
# 真の値と推定値のプロットを並べて表示
# 上段: 真の分布, 下段: GWRによる推定分布
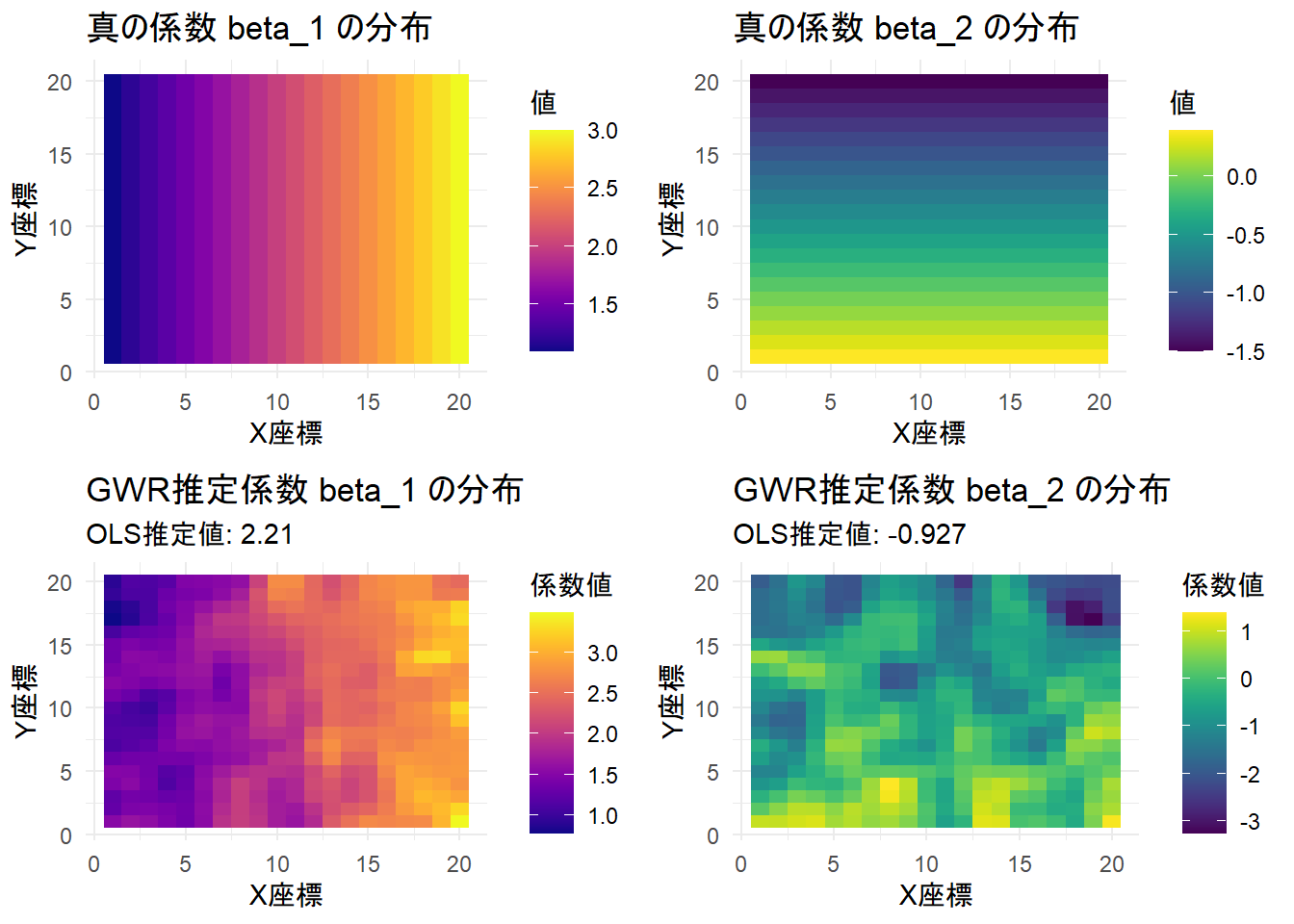
grid.arrange(p_true1, p_true2, p_est1, p_est2, ncol = 2)全体構成
- 左列 (\(\beta_1\) の比較): X座標(東西方向)に依存する係数。
- 右列 (\(\beta_2\) の比較): Y座標(南北方向)に依存する係数。
- 色の意味: 黄色が「高い値(プラスの影響)」、紫・青色が「低い値(マイナスの影響)」を表しています。
左列:\(\beta_1\) の分布(東西の勾配)
- 上段(真の値): 左端(西)が紫色で、右端(東)に向かって滑らかに黄色へと変化しています。これは「東に行くほど説明変数 \(X_1\) の影響力が強くなる」という設定を表しています。
- 下段(GWR推定値): 上段のグラデーションを再現しています。 サブタイトルにある OLS推定値: 2.21 という数字は、この地図全体を「平均的なオレンジ色一色」で塗ることになります。しかし、GWRの結果を見れば、西側では1.0付近(青紫)、東側では3.0付近(黄色)と、場所によって異なる値を取ることが確認でき、\(\beta_1\) の空間的異質性を捉えていると言えます。
右列:\(\beta_2\) の分布(南北の勾配)
- 上段(真の値): 下端(南)が黄色で、上端(北)に向かって青色へと変化しています。こちらは「南に行くほど \(X_2\) の影響がポジティブで、北に行くほどネガティブになる」という設定です。
- 下段(GWR推定値): こちらも、上段の傾向を捉えています。 データに含まれる乱数(ノイズ)の影響で、上段ほど滑らかではなく、多少の斑点(推定誤差)は見られますが、「下が高く上が低い」という構造は復元されています。 OLS推定値 -0.927 だけでは、「南側では係数がプラスである(黄色)」という事実を見落としてしまいますが、GWRはその事実を可視化できています。
以上です。