Rの関数から gwr.sel {spgwr} を確認します。
本ポストはこちらの続きです。

Rの関数:gwr {spgwr}
const typesetMath = (el) => { if (window.MathJax) { // MathJax Typeset window.MathJax.typeset(); } else if (window.katex...
関数 gwr.sel とは
gwr.sel は、地理的加重回帰(GWR)モデルにおいて、ハイパーパラメータである「最適なバンド幅(bandwidth)」を自動的に選択するための関数です。
GWRでは、対象地点に近いデータほど大きな重みを与えますが、「どのくらいの範囲(距離)を『近い』とみなすか」を決めるのがバンド幅です。
このバンド幅が狭すぎると過学習(ノイズまで拾う)し、広すぎると通常の回帰分析(OLS)に近づきすぎて地域特性を見逃します。
gwr.sel は、以下のいずれかの基準を最小化するように、数値最適化アルゴリズムを用いて最適なバンド幅を探索します。
- CV (Cross-Validation): 交差検証スコア。予測精度を重視する場合に用います。
- AIC (Akaike Information Criterion): 赤池情報量基準。モデルの当てはまりと複雑さのバランスを重視する場合に用います。
関数 gwr.sel の引数
library(spgwr)
args(gwr.sel)function (formula, data = list(), coords, adapt = FALSE, gweight = gwr.Gauss,
method = "cv", verbose = TRUE, longlat = NULL, RMSE = FALSE,
weights, tol = .Machine$double.eps^0.25, show.error.messages = FALSE)
NULL- formula
- 回帰モデルの構造を指定する式(例:
y ~ x1 + x2)。 - 最適化の基準となるGWRモデルの従属変数と説明変数を定義します。
- 回帰モデルの構造を指定する式(例:
- data
-
formulaで使用する変数を含むデータフレーム。 - 分析対象のデータセットを提供します。
-
- coords
- 各観測地点の座標行列(2列の行列またはデータフレーム)。
- 地点間の距離を計算するために不可欠な情報です。
- adapt
- 適応型バンド幅(Adaptive Bandwidth)を使用するかどうかの論理値。
-
FALSE(デフォルト): 固定型バンド幅を探索します。出力は物理的な「距離」(例: 500メートル)となります。 -
TRUE: 適応型バンド幅を探索します。出力は全データに対する近傍点の「割合」(例: 0.05 = 近い順に5%のデータを使う)となります。データ密度が不均一な場合に推奨されます。
- gweight
- 重み付けに使用するカーネル関数。デフォルトは
gwr.Gauss(ガウシアンカーネル)。 - 距離減衰の形状を定義します。他にも
gwr.bisquareなどが利用可能です。
- 重み付けに使用するカーネル関数。デフォルトは
- method
- 最適化の基準。
"cv"(交差検証)または"aic"(AIC)。デフォルトは"cv"。 - 何を以て「最適」とするかを決定します。一般に予測目的であればCV、説明・推論目的であればAICが利用されます。
- 最適化の基準。
- verbose
- 探索過程を表示するかどうかの論理値。デフォルトは
TRUE。 -
TRUEの場合、最適化の各ステップにおけるバンド幅の値と、その時のスコア(CV値またはAIC値)が出力されます。収束状況を確認するために有用です。
- 探索過程を表示するかどうかの論理値。デフォルトは
- longlat
- 座標が経度・緯度であるかを示す論理値。
-
TRUEの場合、地球の曲面を考慮した大圏距離(Great Circle Distance)で計算を行います。
- RMSE
-
method="cv"の際、スコアとして二乗和(RSS)ではなく二乗平均平方根誤差(RMSE)を返すかどうかの論理値。 - 出力されるスコアの単位を調整するもので、最適化の結果(選ばれるバンド幅)自体には影響しません。
-
- weights
- 観測値ごとの重み(数値ベクトル)。
- 地理的な重みとは別に、データの信頼性などを考慮する場合に使用します。
- tol
- 最適化の収束判定基準(許容誤差)。
- 探索をどの程度の精度で終了するかを制御します。
- show.error.messages
- 内部最適化関数
optimizeからのエラーを表示するかどうか。 - デバッグ用です。
- 内部最適化関数
シミュレーション用サンプルデータとコード
gwr.sel の機能を確認するため、以下のシミュレーションを行います。
- データ生成:
- \(20 \times 20\) のグリッド上で、中心 \((10, 10)\) からの距離に応じて係数が波紋(同心円)状に変化するような空間構造を持つデータを生成します。
- 固定型バンド幅の探索 (
adapt=FALSE):- 物理的な距離として最適なバンド幅を探索します。
- 適応型バンド幅の探索 (
adapt=TRUE):- 近傍点の割合として最適なバンド幅を探索します。
- 結果の検証:
-
gwr.selで得られた最適値を用いてgwrを実行し、真の係数分布を復元できるか確認します。
-
以下はRコードです。
空間構造とサンプルデータの作成
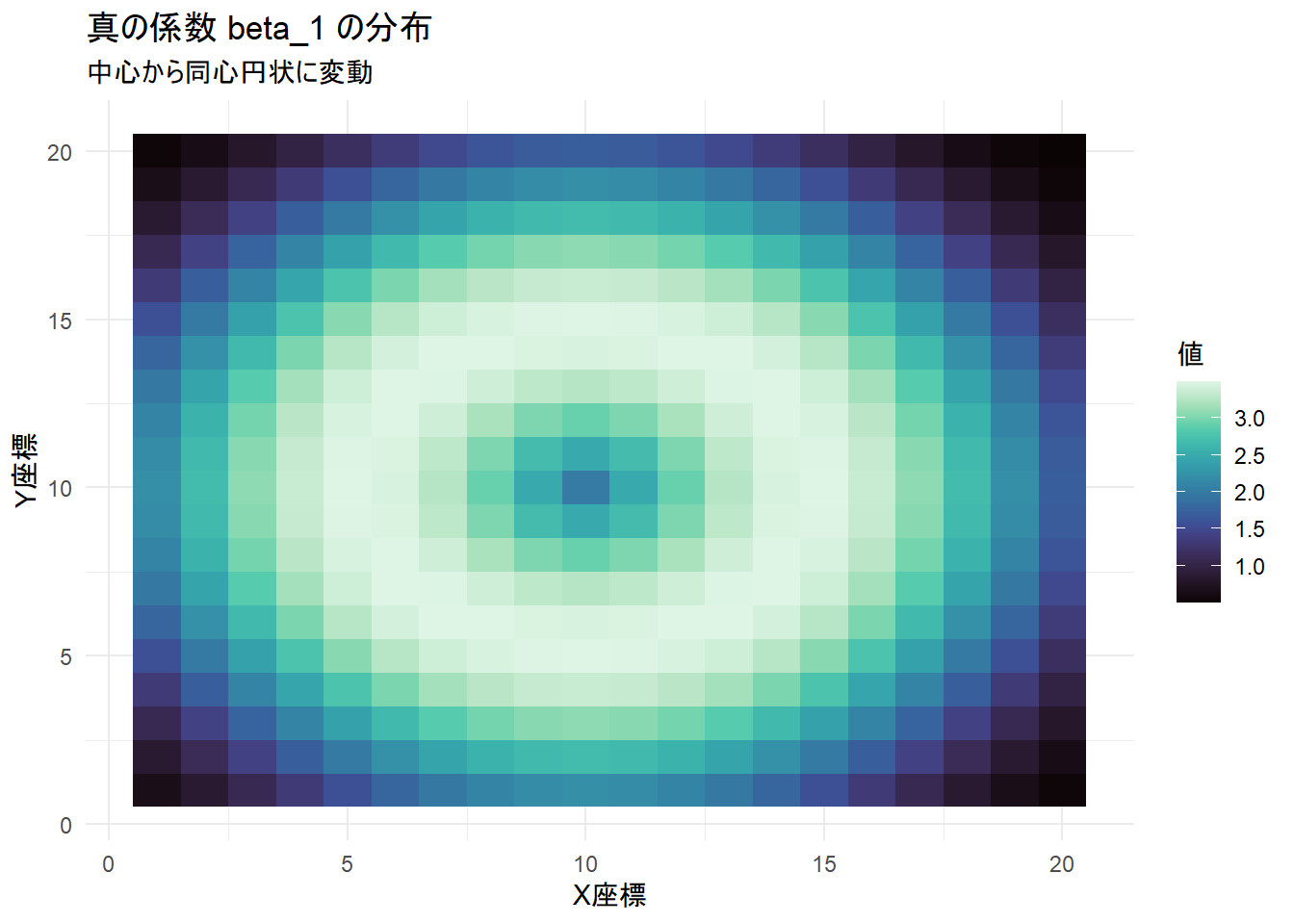
中心 \((10, 10)\) からの距離に応じてサインカーブを描くように係数 \(\beta_1\) を変化させ、単調な東西・南北の勾配よりも複雑な「同心円状」の空間構造を作成し、GWRの性能を試します。
# 必要なパッケージの読み込み
library(spgwr)
library(ggplot2)
library(viridis)
library(gridExtra)
# 乱数シードの固定
seed <- 20251205
set.seed(seed)
# グリッドサイズの設定(20x20 = 400地点)
# 各セルの間隔は 1 単位とします
side_length <- 20
n <- side_length * side_length
# 座標データの作成
coords <- expand.grid(x = 1:side_length, y = 1:side_length)
coords_mat <- as.matrix(coords)
# 説明変数 X1 の生成
X1 <- runif(n, 0, 10)
# 真の係数の設定
# beta_0 (切片): 定数
beta_0_true <- 5.0
# beta_1 (傾き): 空間的に複雑に変化させる
# 中心 (10, 10) からの距離に応じて波紋のように係数が変化する設定
dist_from_center <- sqrt((coords$x - 10)^2 + (coords$y - 10)^2)
beta_1_true <- 2.0 + sin(dist_from_center / 3) * 1.5
# 結果として、beta_1 は 0.5 ~ 3.5 の間で変動します
# 従属変数 y の生成
# y = beta_0 + beta_1(u,v) * X1 + error
epsilon <- rnorm(n, mean = 0, sd = 1.0)
y <- beta_0_true + beta_1_true * X1 + epsilon
# データフレームの作成
sim_data <- data.frame(
y = y,
x1 = X1,
coord_x = coords$x,
coord_y = coords$y
)
cat("--- 作成したサンプルデータの一部を確認 ---\n")
print(str(sim_data))--- 作成したサンプルデータの一部を確認 ---
'data.frame': 400 obs. of 4 variables:
$ y : num 7.18 8.57 8.42 7.59 9.73 ...
$ x1 : num 4.888 3.514 3.213 0.766 2.825 ...
$ coord_x: int 1 2 3 4 5 6 7 8 9 10 ...
$ coord_y: int 1 1 1 1 1 1 1 1 1 1 ...
NULL真の係数分布の可視化
gwr.sel による最適バンド幅の探索
固定型バンド幅 (Fixed Bandwidth) の探索
ここでは固定距離の最適値を探索します。
verbose = TRUE により、探索の過程が出力されます。出力される数値の左側が「試行されたバンド幅(距離)」、右側が「その時のCVスコア」です。CVスコアが最小になる距離に収束していく様子が確認できます。
# method = "cv" (交差検証) を使用
# verbose = TRUE なので、探索過程(距離とCV値)が表示されます
cat("(A) 固定型バンド幅 (adapt=FALSE) の探索\n\n")
bw_fixed <- gwr.sel(y ~ x1,
data = sim_data, coords = coords_mat,
adapt = FALSE, method = "cv", verbose = TRUE
)
cat(sprintf("\n=> 決定された最適固定バンド幅 (距離): %.4f\n", bw_fixed))(A) 固定型バンド幅 (adapt=FALSE) の探索
Bandwidth: 10.28006 CV score: 10064.04
Bandwidth: 16.61687 CV score: 10458.97
Bandwidth: 6.363687 CV score: 8422.505
Bandwidth: 3.943238 CV score: 5242.529
Bandwidth: 2.447319 CV score: 2509.161
Bandwidth: 1.52279 CV score: 1192.317
Bandwidth: 0.9513992 CV score: 860.0891
Bandwidth: 0.7211472 CV score: 894.9843
Bandwidth: 0.9191465 CV score: 857.4664
Bandwidth: 0.9007033 CV score: 856.9681
Bandwidth: 0.8973097 CV score: 856.9587
Bandwidth: 0.8977528 CV score: 856.9584
Bandwidth: 0.8977935 CV score: 856.9584
Bandwidth: 0.8977121 CV score: 856.9584
Bandwidth: 0.8977528 CV score: 856.9584
=> 決定された最適固定バンド幅 (距離): 0.8978適応型バンド幅 (Adaptive Bandwidth) の探索
ここでは適応型(割合)の最適値を探索しています。
出力される数値は \(0 \sim 1\) の範囲の割合です。AICが最小になる割合を探索します。
データ密度が均一なグリッドデータであっても、適応型バンド幅は有効に機能します。
# method = "aic" (AIC) を使用
# adapt = TRUE なので、近傍点の割合 (0~1) が探索されます
cat("(B) 適応型バンド幅 (adapt=TRUE) の探索\n\n")
bw_adapt <- gwr.sel(y ~ x1,
data = sim_data, coords = coords_mat,
adapt = TRUE, method = "aic", verbose = TRUE
)
cat(sprintf("\n=> 決定された最適適応バンド幅 (割合): %.4f\n", bw_adapt))
cat(sprintf(" (400地点中、約 %.1f 地点を近傍として使用)\n", bw_adapt * n))(B) 適応型バンド幅 (adapt=TRUE) の探索
Bandwidth: 0.381966 AIC: 2402.622
Bandwidth: 0.618034 AIC: 2419.762
Bandwidth: 0.236068 AIC: 2376.254
Bandwidth: 0.145898 AIC: 2321.672
Bandwidth: 0.09016994 AIC: 2215.451
Bandwidth: 0.05572809 AIC: 2074.609
Bandwidth: 0.03444185 AIC: 1892.875
Bandwidth: 0.02128624 AIC: 1705.205
Bandwidth: 0.01315562 AIC: 1554.94
Bandwidth: 0.008130619 AIC: 1488.348
Bandwidth: 0.005024999 AIC: 1471.734
Bandwidth: 0.003825766 AIC: 1471.708
Bandwidth: 0.004416955 AIC: 1471.708
Bandwidth: 0.00412136 AIC: 1471.708
Bandwidth: 0.004008453 AIC: 1471.708
Bandwidth: 0.003938673 AIC: 1471.708
Bandwidth: 0.003895546 AIC: 1471.708
Bandwidth: 0.003895546 AIC: 1471.708
=> 決定された最適適応バンド幅 (割合): 0.0039
(400地点中、約 1.6 地点を近傍として使用)最適バンド幅を用いたGWRの実行と評価
ここでは (B) で求めた適応型バンド幅を使用してモデルを当てはめます
model_gwr <- gwr(y ~ x1,
data = sim_data, coords = coords_mat,
adapt = bw_adapt, hatmatrix = TRUE, se.fit = TRUE
)
# 結果のデータフレーム化 (座標を追加)
results_df <- as.data.frame(model_gwr$SDF)
results_df$coord_x <- sim_data$coord_x
results_df$coord_y <- sim_data$coord_y推定結果の可視化
# GWRによる推定係数 beta_1
p_est <- ggplot(results_df, aes(x = coord_x, y = coord_y, fill = x1)) +
geom_tile() +
scale_fill_viridis(option = "mako") +
labs(
title = "GWR推定係数 beta_1 の分布",
subtitle = paste("適応型バンド幅:", round(bw_adapt, 4)),
x = "X座標", y = "Y座標", fill = "値"
) +
theme_minimal()
# 並べて表示
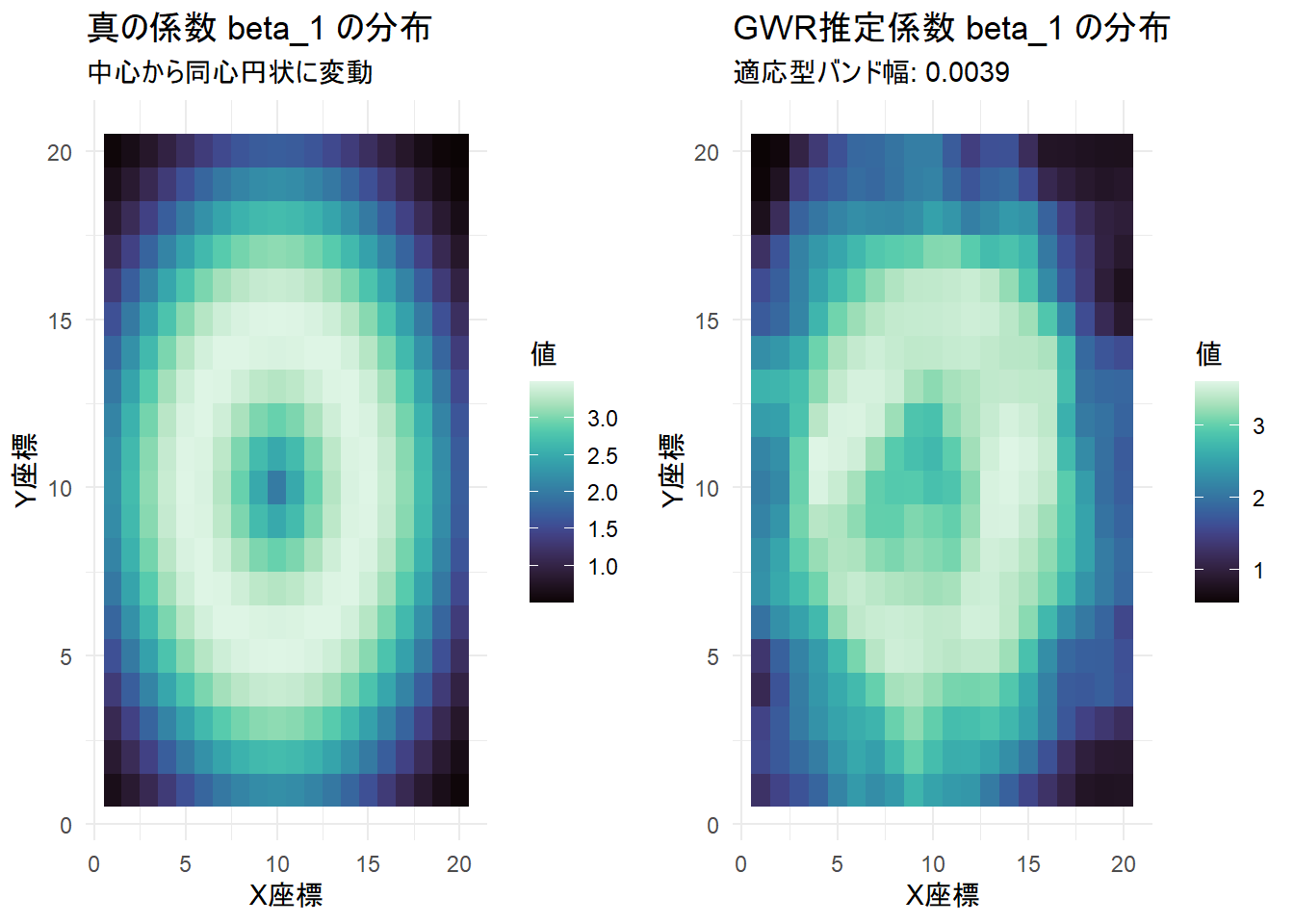
grid.arrange(p_true, p_est, ncol = 2)Figure 2 の構成
- 左図(真の係数 beta_1 の分布):
- シミュレーションの設計図である「正解」データです。中心 \((10, 10)\) からの距離に応じて、係数が低い(濃い青)→高い(薄い緑・白)→低い(濃い青)と波紋のように同心円状に変化する構造を持っています。
- 右図(GWR推定係数 beta_1 の分布):
- 観測データのみからGWRによって計算された「推定」結果です。上部に
gwr.selが算出した「適応型バンド幅: 0.0039」が表示されています。
- 観測データのみからGWRによって計算された「推定」結果です。上部に
視覚的評価と gwr.sel の貢献
- 複雑なパターンの復元:
- 単調な東西・南北の勾配ではなく、ドーナツ状(同心円状)という非線形な空間パターンを捉えています。中心部の低い値の「穴」、その周囲を取り巻く高い値の「リング」、そして四隅の低い値へ戻るグラデーションが、右図でも確認できます。
- 最適バンド幅の役割:
- AICを最小化する計算プロセスを通じ、サブタイトルにある
0.0039(全データの約0.4%)という小さなバンド幅が選択されて、非線形なパターンが捉えられています。もしgwr.selが大きなバンド幅を選択していた場合、局所的な変動が平滑化されすぎてしまい、このような細かいリング構造はぼやけて消失していたでしょう。逆に、小さすぎればノイズだらけの図になっていたはずです。
- AICを最小化する計算プロセスを通じ、サブタイトルにある
以上です。