Rの関数:commarobust {estimatr}

# パッケージの読み込み
library(ggplot2)
library(dplyr)

# 乱数シードの固定（再現性のため）
seed <- 20251210
set.seed(seed)

# サンプルサイズの定義
N <- 200

# データの生成
# 説明変数 X: 一様分布から生成
X <- runif(N, min = 1, max = 10)

# 誤差項 e: 分散が X に依存するように作成（不均一分散）
# Xが大きいほどばらつき（標準偏差）が大きくなる
e <- rnorm(N, mean = 0, sd = X * 1.5)

# 被説明変数 y: 真のモデル y = 2 + 3*X + e
y <- 2 + 3 * X + e

# データフレーム化
df_hetero <- data.frame(y = y, X = X)

# データの可視化
# じょうご型に広がっている様子を確認
p1 <- ggplot(df_hetero, aes(x = X, y = y)) +
  geom_point(alpha = 0.6) +
  geom_smooth(method = "lm", se = FALSE, color = "blue") +
  labs(
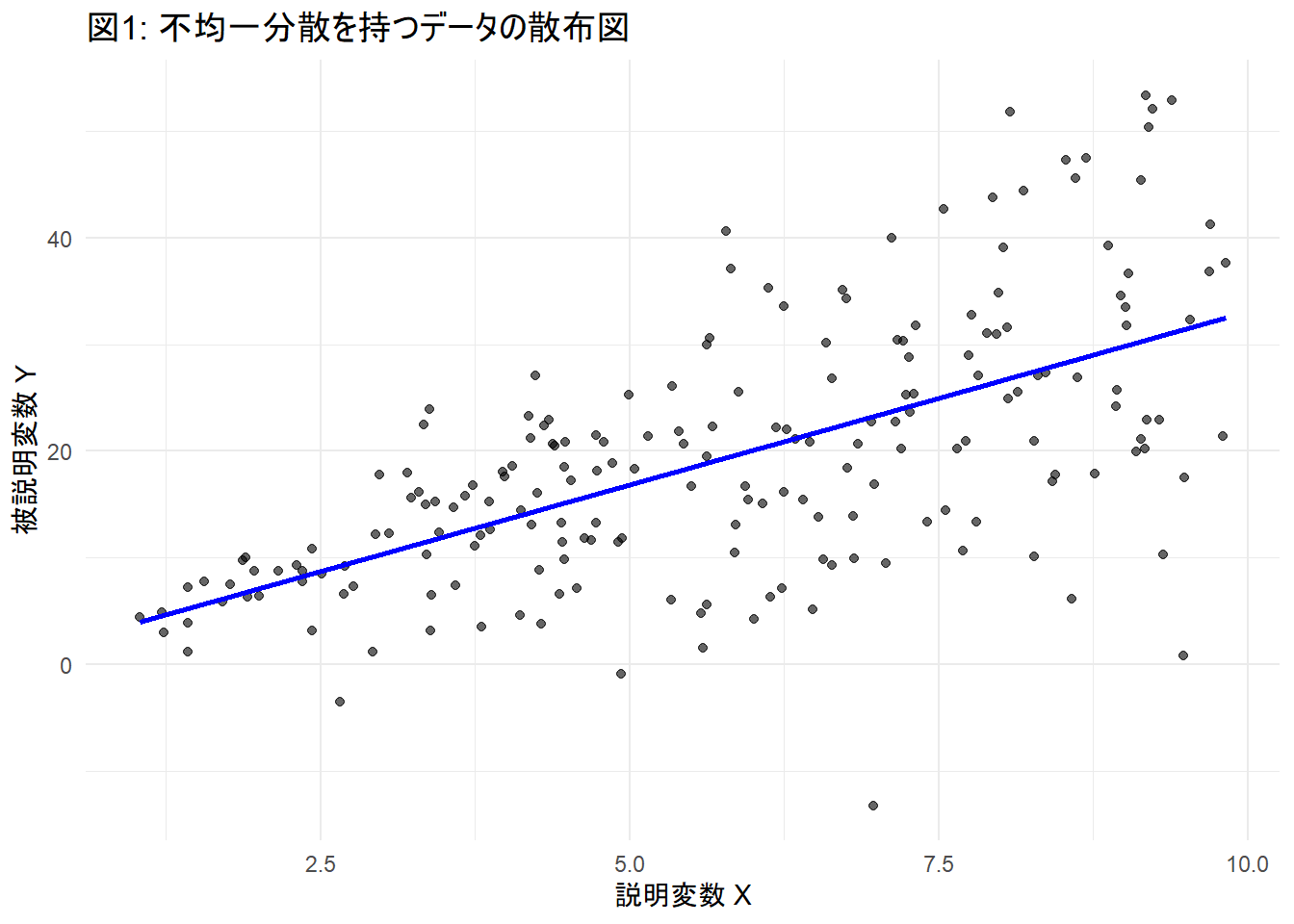
    title = "図1: 不均一分散を持つデータの散布図",
    x = "説明変数 X",
    y = "被説明変数 Y"
  ) +
  theme_minimal()

print(p1)

set.seed(seed)

# クラスター設定
n_clusters <- 20 # クラスター数（例: 20の学校）
n_per_cluster <- 10 # 1クラスターあたりの観測数（例: 1校あたり10人の生徒）
N_cluster <- n_clusters * n_per_cluster

# クラスターIDの生成
cluster_id <- rep(1:n_clusters, each = n_per_cluster)

# クラスターごとの説明変数（例: 学校の質）
# 同じクラスター内の個体は同じ値を持つ部分があるとする
X_cluster_level <- rep(rnorm(n_clusters), each = n_per_cluster)

# 個体レベルのノイズ
X_individual <- rnorm(N_cluster)

# 最終的な説明変数 X
X_cl <- X_cluster_level + X_individual

# クラスター固有の誤差（ランダム効果のようなもの）
# 同じクラスター内の個体は、この誤差を共有する（相関が生じる）
cluster_error <- rep(rnorm(n_clusters, sd = 2), each = n_per_cluster)

# 個体固有の誤差
individual_error <- rnorm(N_cluster, sd = 1)

# 被説明変数 y: 真の係数は 1
# y = 1 * X + (クラスター誤差 + 個体誤差)
y_cl <- 1 * X_cl + cluster_error + individual_error

# データフレーム化
df_cluster <- data.frame(y = y_cl, X = X_cl, cluster_id = factor(cluster_id))

# モデル（通常のOLS）から残差を取得し、データフレームに追加
# 通常の lm 関数で推定（独立を仮定）
model_cl_ols <- lm(y ~ X, data = df_cluster)

df_cluster$residuals <- resid(model_cl_ols)

# クラスターID順ではなく、残差の中央値順に並べ替えて見やすくする
# （平均的にプラスの誤差を持つクラスターと、マイナスの誤差を持つクラスターを整理）
df_cluster$cluster_ordered <- reorder(df_cluster$cluster_id, df_cluster$residuals, FUN = median)

# クラスターごとの残差の箱ひげ図
p2 <- ggplot(df_cluster, aes(x = cluster_ordered, y = residuals, fill = cluster_ordered)) +
  geom_hline(yintercept = 0, linetype = "dashed", color = "gray50", linewidth = 1) + # ゼロの基準線
  geom_boxplot(alpha = 0.7, show.legend = FALSE) + # 箱ひげ図
  labs(
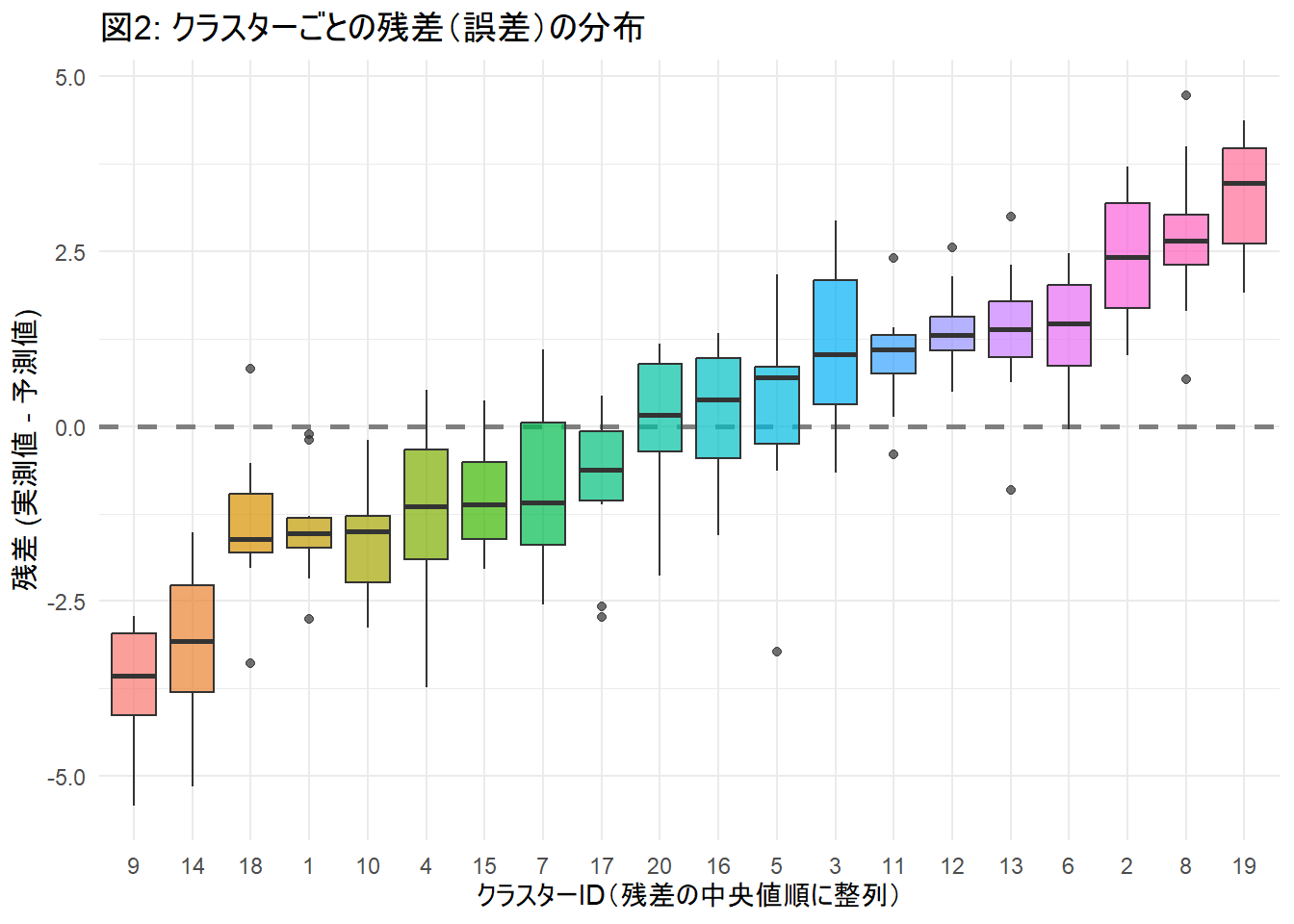
    title = "図2: クラスターごとの残差（誤差）の分布",
    x = "クラスターID（残差の中央値順に整列）",
    y = "残差 (実測値 - 予測値)"
  ) +
  theme_minimal() +
  theme(axis.text.x = element_text(angle = 0, vjust = 0.5))

print(p2)