Rの関数から lm_robust {estimatr} を確認します。
本ポストはこちらの続きです。

関数 lm_robust とは
lm_robust は、線形回帰モデル(Linear Regression Model)の推定を行うと同時に、様々なタイプの「頑健標準誤差(Robust Standard Errors)」を算出するための関数です。
Rの標準関数である lm は、誤差項が等分散(homoskedasticity)であり、かつ観測値が独立であることを仮定しています。
しかし、実データにおいては不均一分散(heteroskedasticity)や、観測データ間の相関(クラスター相関)が存在する場合が多くあります。
このような状況下で lm を使用すると、標準誤差が不正確になり、検定結果(p値や信頼区間)の信頼性が損なわれます。
lm_robust は、デフォルトで不均一分散に対して頑健な標準誤差(HC2)を出力します。
また、引数を指定するだけで、クラスターロバスト標準誤差の計算や、固定効果(Fixed Effects)モデルの推定を行うことが可能です。
関数 lm_robust の引数
library(estimatr)
args(lm_robust)function (formula, data, weights, subset, clusters, fixed_effects,
se_type = NULL, ci = TRUE, alpha = 0.05, return_vcov = TRUE,
try_cholesky = FALSE)
NULL-
formula- 解析モデルを指定する式です。形式は
y ~ x1 + x2のように記述します。 - 被説明変数と説明変数の関係性を定義します。
- 解析モデルを指定する式です。形式は
-
data-
formulaで指定された変数を含むデータフレームです。 - 解析対象のデータセットを関数に渡します。
-
-
weights- 重み付き最小二乗法(WLS)を行う際の重みを指定するベクトルです。
- 調査データのサンプリングウェイトなどを適用する場合に使用します。
-
subset- 分析に使用するデータの部分集合(サブセット)を指定する条件式です。
- 特定の条件(例:男性のみ、2000年以降など)に合致するデータのみで分析を行う際に利用します。
-
clusters- クラスター変数を指定します。
- データがグループ構造(学校、地域、企業など)を持つ場合、グループ内の誤差相関を考慮した「クラスターロバスト標準誤差」を計算するために使用します。
-
fixed_effects- 固定効果として扱う変数を指定します。形式は
~ group_idのように記述します。 - グループごとの固有の効果(切片の違い)を制御します。
- 固定効果として扱う変数を指定します。形式は
-
se_type- 標準誤差の計算タイプを指定する文字列です。
- デフォルト:
NULL(クラスター指定がない場合は"HC2"、ある場合は"CR2"が自動選択されます)。 - 選択肢:
-
"HC0"~"HC3": 不均一分散頑健標準誤差。 -
"CR0","CR2": クラスターロバスト標準誤差。 -
"classical": 通常のlmと同じ等分散仮定の標準誤差。 -
"stata": Stata のデフォルト設定(HC1やCR1に相当)と同等の計算。
-
-
ci- 信頼区間(Confidence Interval)を計算するかどうかの論理値(
TRUE/FALSE)です。 - デフォルト:
TRUE
- 信頼区間(Confidence Interval)を計算するかどうかの論理値(
-
alpha- 有意水準を指定する数値です。
- デフォルト:
0.05(95%信頼区間を計算)。
-
return_vcov- 分散共分散行列(Variance-Covariance Matrix)を結果オブジェクトに含めるかどうかの論理値です。
- デフォルト:
TRUE - 後の分析や他の関数で分散共分散行列が必要な場合に利用します。
-
try_cholesky- 行列の分解にコレスキー分解を試みるかどうかの論理値です。
- デフォルト:
FALSE
シミュレーションコード
以下に、lm_robust の機能を確認するためのサンプルデータを用いたシミュレーションコードを示します。
このシミュレーションでは、以下の特徴を持つデータを生成し、通常の lm と lm_robust の違いを確認にします。
- 不均一分散(Heteroskedasticity):
- 説明変数の値が大きくなるにつれて、誤差のバラつきが大きくなる。
- クラスター相関(Clustering):
- データが複数のグループ(店舗)に分かれており、同じ店舗内のデータは似通っている。
この状況下では、通常の lm は標準誤差を過小評価(精度が高いと評価)しがちですが、lm_robust はこれを適切に補正することを確認します。
シミュレーションデータの生成
- 特徴1: 広告費が増えるほど、売上のばらつきが大きくなる (不均一分散)
- 特徴2: 店舗ごとに売上のベースラインが異なる (クラスター構造)
# パッケージの読み込み
library(ggplot2)
library(dplyr)
library(texreg) # 結果比較用
# 乱数シードの固定
seed <- 20251218
set.seed(seed)
# 設定: 小売チェーン店の広告効果分析
# N: 総観測数
# n_stores: 店舗数(クラスター数)
n_stores <- 50
n_obs_per_store <- 20
N <- n_stores * n_obs_per_store
# データフレーム作成
df_sim <- data.frame(
store_id = rep(1:n_stores, each = n_obs_per_store)
)
# 1. 説明変数 X (広告費): 一様分布
df_sim$ad_spend <- runif(N, min = 10, max = 100)
# 2. クラスター効果 (店舗ごとの固有要因)
# 店舗ごとにベースの売上が異なる
store_effect <- rnorm(n_stores, mean = 0, sd = 10)
df_sim$store_intercept <- store_effect[df_sim$store_id]
# 3. 誤差項 (不均一分散 + クラスター相関)
# 不均一分散: 広告費が多いほど、売上のブレ(分散)が大きくなる
# クラスター相関: 同じ店舗内では誤差の方向が似る(ここでは簡易的にstore_interceptで表現済みだが、さらにノイズを加える)
# heteroskedastic_error: Xが大きいほどSDが大きい
hetero_error <- rnorm(N, mean = 0, sd = df_sim$ad_spend * 0.5)
# 4. 被説明変数 Y (売上)
# True Model: Sales = 500 + 5 * Ad_Spend + Store_Effect + Error
true_beta <- 5
df_sim$sales <- 500 + (true_beta * df_sim$ad_spend) + df_sim$store_intercept + hetero_error
cat("--- データ概要 ---\n")
cat(sprintf("観測数: %d (店舗数: %d)\n", N, n_stores))--- データ概要 ---
観測数: 1000 (店舗数: 50)シミュレーションデータの可視化
# データの可視化(不均一分散の確認)
p1 <- ggplot(df_sim, aes(x = ad_spend, y = sales)) +
geom_point(alpha = 0.5, color = "darkblue") +
geom_smooth(method = "lm", color = "red", se = FALSE) +
labs(
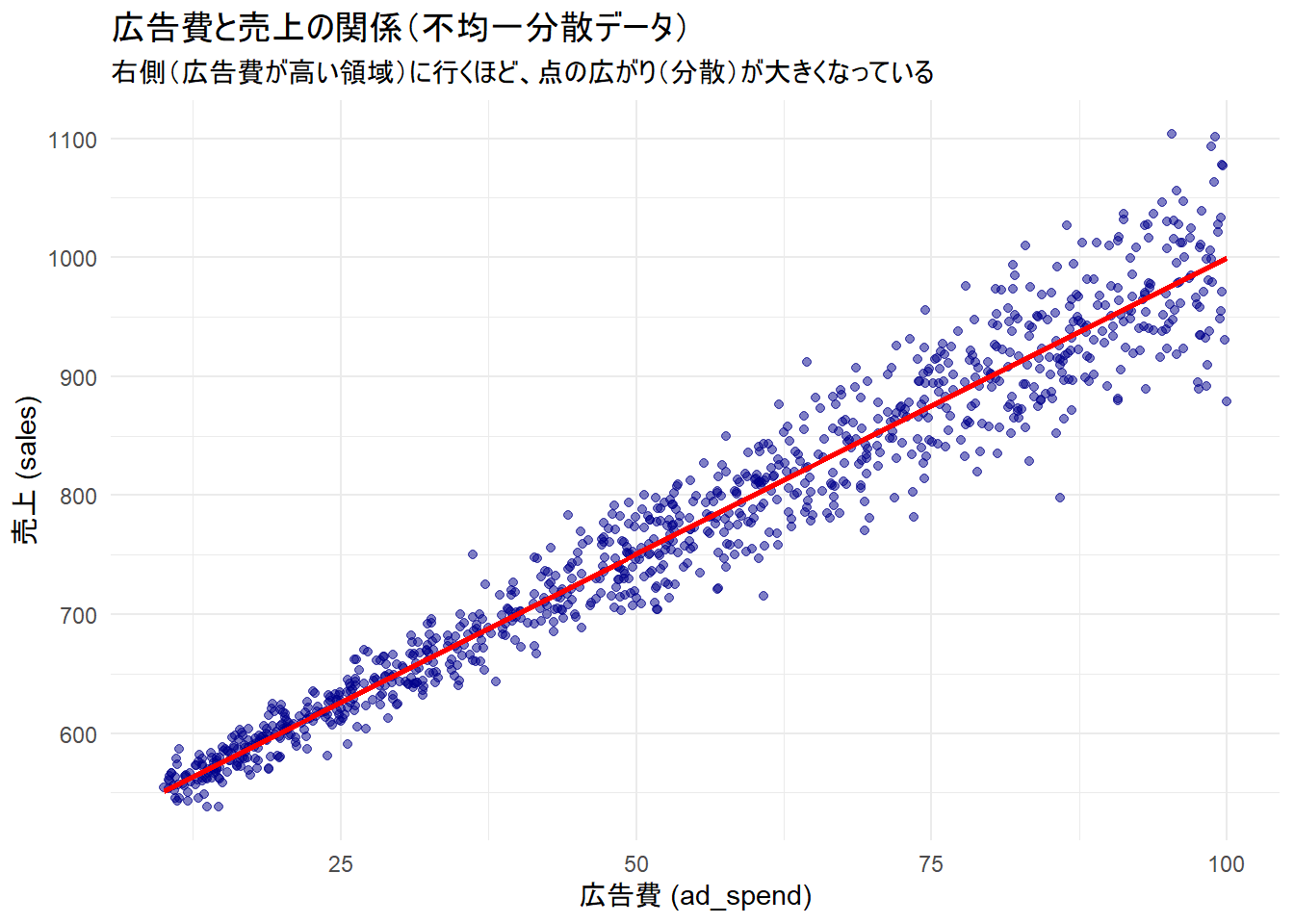
title = "広告費と売上の関係(不均一分散データ)",
subtitle = "右側(広告費が高い領域)に行くほど、点の広がり(分散)が大きくなっている",
x = "広告費 (ad_spend)",
y = "売上 (sales)"
) +
theme_minimal()
print(p1)モデル推定と標準誤差の比較
# モデル1: 通常の lm (等分散・独立を仮定)
model_ols <- lm(sales ~ ad_spend, data = df_sim)
# モデル2: lm_robust (デフォルト = HC2: 不均一分散に対処)
# クラスターは指定せず、個体ごとの不均一分散のみ考慮
model_robust_hc2 <- lm_robust(sales ~ ad_spend, data = df_sim, se_type = "HC2")
# モデル3: lm_robust (クラスターロバスト = CR2: クラスター相関に対処)
# 店舗IDをクラスターとして指定
model_robust_cluster <- lm_robust(sales ~ ad_spend, data = df_sim, clusters = store_id, se_type = "CR2")
cat("--- 推定結果の比較 ---")
# texregを使って見やすく並べる
screenreg(
list(model_ols, model_robust_hc2, model_robust_cluster),
custom.model.names = c("通常のlm", "lm_robust(HC2)", "lm_robust(Cluster)"),
include.ci = FALSE,
digits = 3
)
cat("\n--- 標準誤差の比較 ---\n")
# 係数と標準誤差の抽出
se_ols <- summary(model_ols)$coefficients["ad_spend", "Std. Error"]
se_hc2 <- summary(model_robust_hc2)$coefficients["ad_spend", "Std. Error"]
se_cl <- summary(model_robust_cluster)$coefficients["ad_spend", "Std. Error"]
cat(sprintf("1. 通常のlmの標準誤差 : %.4f\n", se_ols))
cat(sprintf("2. 頑健(HC2)の標準誤差 : %.4f\n", se_hc2))
cat(sprintf("3. クラスター頑健の標準誤差 : %.4f\n\n", se_cl))--- 推定結果の比較 ---
=============================================================
通常のlm lm_robust(HC2) lm_robust(Cluster)
-------------------------------------------------------------
(Intercept) 500.973 *** 500.973 *** 500.973 ***
(2.176) (1.663) (2.172)
ad_spend 4.988 *** 4.988 *** 4.988 ***
(0.036) (0.040) (0.042)
-------------------------------------------------------------
R^2 0.950 0.950 0.950
Adj. R^2 0.950 0.950 0.950
Num. obs. 1000 1000 1000
RMSE 30.119 30.119
N Clusters 50
=============================================================
*** p < 0.001; ** p < 0.01; * p < 0.05
--- 標準誤差の比較 ---
1. 通常のlmの標準誤差 : 0.0362
2. 頑健(HC2)の標準誤差 : 0.0401
3. クラスター頑健の標準誤差 : 0.0419推定値(Estimate)
表の Estimate 行(係数)を確認しますと、(Intercept) は 500.973、ad_spend は 4.988 であり、3つのモデルすべてにおいて一致しています。
- 通常のlm: 500.973 / 4.988
- lm_robust(HC2): 500.973 / 4.988
- lm_robust(Cluster): 500.973 / 4.988
「頑健標準誤差(Robust SE)は、回帰直線の傾きや切片そのものを変更するわけではない」ため、どの手法を用いても、最小二乗法(OLS)によってデータの中心を通る直線を引くプロセスは同一です。
異なるのは、その推定値に対する「確信の度合い(標準誤差)」の評価方法のみです。
標準誤差(Standard Error)
- 通常のlm (0.0362): 最も小さい(過小評価)
- 通常の
lmは、「すべてのデータにおける誤差の分散は一定であり、かつすべてのデータは独立である」という仮定を置いています。シミュレーションデータには不均一分散とクラスター相関が含まれているにもかかわらず、lmはこれらを無視します。
- 通常の
- lm_robust(HC2) (0.0401): 不均一分散への対処
- ここでは、不均一分散(広告費が増えると売上のブレが大きくなる現象)を考慮して補正が行われました。データのばらつきが激しい部分の影響を適切に割り引いて評価した結果、標準誤差は
lmよりも大きく(保守的に)なりました。
- ここでは、不均一分散(広告費が増えると売上のブレが大きくなる現象)を考慮して補正が行われました。データのばらつきが激しい部分の影響を適切に割り引いて評価した結果、標準誤差は
- lm_robust(Cluster) (0.0419): クラスター相関への対処
- ここではさらに、「同じ店舗内のデータは似通っている」というクラスター相関まで考慮されています。データは1000行ありますが、実質的な情報の単位は「50店舗」分に近いと判断されます。有効なサンプルサイズが減少したのと同等の扱いとなるため、標準誤差はさらに拡大し、3つのモデルの中で最も大きな値となりました。
結論
このシミュレーション結果は、以下のリスクを浮き彫りにしています。
もし分析者がデータの特性(不均一分散やクラスター構造)を無視して通常の lm を使用した場合、標準誤差を 0.0362 と見積もります。
しかし、より現実に即したクラスターロバスト推定では 0.0419 です。
今回は、いずれのモデルでもp値は設定した有意水準を下回りましたが、もし係数がボーダーライン上の値であった場合、実際に存在する不均一分散とクラスター相関を考慮した lm_robust では「有意ではない」と判定される場合でも、lm では「有意である」と誤って判定してしまう結果を招きます。
固定効果モデルのデモンストレーション
引数 Fixed Effects(固定効果モデル)を利用して、店舗ごとの固有効果(intercept)を制御する場合を確認します。
# fixed_effects 引数を利用
model_fe <- lm_robust(sales ~ ad_spend, data = df_sim, fixed_effects = ~store_id, clusters = store_id)
print(summary(model_fe))
Call:
lm_robust(formula = sales ~ ad_spend, data = df_sim, clusters = store_id,
fixed_effects = ~store_id)
Standard error type: CR2
Coefficients:
Estimate Std. Error t value Pr(>|t|) CI Lower CI Upper DF
ad_spend 4.991 0.04107 121.5 4.397e-60 4.908 5.074 46.71
Multiple R-squared: 0.9555 , Adjusted R-squared: 0.9532
Multiple R-squared (proj. model): 0.9533 , Adjusted R-squared (proj. model): 0.9508
F-statistic (proj. model): 1.477e+04 on 1 and 49 DF, p-value: < 2.2e-16「店舗固有の事情」を排除した推定(Estimate)
係数 ad_spend の推定値は 4.991 となりました。
これまでのモデル(約4.988)とわずかに値が異なります。
これは、推定手法が「プールされたOLS(全体をまとめて分析)」から「固定効果モデル(Within推定)」へと変化したためです。
- メカニズム:
-
fixed_effects = ~store_idを指定したことで、モデルは「店舗ごとの売上の平均的な高さ(立地が良い、店長が優秀など)」をコントロール(除去)しました。
-
- 解釈:
- 「ある店舗の中で広告費を増やしたとき、その店舗の売上がどれだけ伸びるか」という、店舗内(Within)の変動のみに注目して係数を算出しています。
- 意義:
- もし「広告費が多い店舗は、たまたま立地も良い」といった相関があった場合、通常のOLSではバイアスが生じますが、固定効果モデルはそのような「店舗固有の不変な要因」によるバイアスをシャットアウトできます。
クラスター数に基づいた自由度の調整(DF)
自由度(DF)が 46.71 となっています。
- 観測数は1000ですが、自由度は998ではありません。
- クラスター数が50(店舗)であるため、実質的な情報の独立性は「50」に近い水準まで下がります。
以上です。