Rの関数:Fstats {strucchange}

Rの関数から Fstats {strucchange} を確認します。

関数 `Fstats` とは

Fstats は、回帰モデルにおける「構造変化（Structural Change）」を検出するために、F統計量の一連のプロセスを計算する関数です。

時系列データ分析において、ある時点を境にデータの傾向（パラメータ）がガラリと変わってしまうことを構造変化と呼びます。

例えば、経済危機や政策変更の前後で、経済モデルの係数が変化するようなケースです。

通常、変化点が既知であれば「Chow検定」を行いますが、Fstats は変化点が未知である場合に対応します。

具体的には、設定された区間内のあらゆる時点を「潜在的な変化点」と仮定してF検定（Chow検定）を繰り返し行い、その統計量の推移を出力します。

このF統計量が最大となる地点が、最も尤もらしい構造変化の候補点となります。

関数 `Fstats` の引数

library(strucchange)
args(Fstats)

function (formula, from = 0.15, to = NULL, data = list(), vcov. = NULL) 
NULL

formula
- 検定対象となる線形回帰モデルの式です（例: y ~ x）。
- 構造変化の有無を検証したい従属変数と説明変数の関係を定義します。
from
- 検定を開始するタイミングを指定します。
- 数値が 1 未満（例: 0.15）の場合はデータの全期間に対する割合（トリミングパラメータ）として解釈され、開始位置が n * from となります。数値が 1 以上の場合は、データのインデックス（何番目のデータか）として直接解釈されます。
- デフォルト: 0.15（データの最初の15%を除外して検定を開始します。構造変化を検定するためには、変化点の前後双方にある程度のサンプル数が必要であり、端点付近では安定した推定ができないためです）。
to
- 検定を終了するタイミングを指定します。
- from と同様に、割合またはインデックスで指定します。NULL の場合は n - from （つまり、from で指定した割合分だけ最後も残す形）となります。
data
- formula で指定された変数を含むデータフレーム、リスト、または時系列オブジェクト（ts）です。
- モデル構築に必要なデータを渡します。
vcov.
- 分散共分散行列を推定する関数を指定します（例: sandwich パッケージの vcovHAC など）。
- デフォルト: NULL（通常のOLS標準誤差を使用）。
- 誤差項に自己相関や不均一分散が存在する場合、通常のF検定は不適切となる可能性があります。そのような場合、ロバストな分散推定量を用いることで検定の妥当性を保ちます。

シミュレーションコード

以下に、Fstats の機能を確認するためのサンプルデータを用いたシミュレーションコードを示します。

このシミュレーションでは、途中で「切片（水準）」と「傾き（トレンド）」が急激に変化する時系列データを作成し、Fstats がその変化点を正しく捉えられるか検証します。

シミュレーションデータの生成

# パッケージの読み込み
library(ggplot2)

# 乱数シードの固定
seed <- 20251224
set.seed(seed)

# 設定: 100期間の時系列データ
# 50時点目を境に構造変化が発生すると想定する
n_obs <- 100
break_point <- 50

# 時間インデックス
time_index <- 1:n_obs

# 前半 (1-50): 緩やかな上昇トレンド
# y = 10 + 0.5 * t + error
y_part1 <- 10 + 0.5 * time_index[1:break_point] + rnorm(break_point, sd = 2)

# 後半 (51-100): 急激な下降トレンド（かつ水準シフト）
# y = 60 - 0.8 * (t - 50) + error
# ※ 50時点目での連続性をあえて持たせず、ジャンプさせる
y_part2 <- 60 - 0.8 * (time_index[(break_point + 1):n_obs] - break_point) + rnorm(n_obs - break_point, sd = 2)

# データの結合
y_total <- c(y_part1, y_part2)
df_sim <- data.frame(
  time = time_index,
  y = y_total
)

# tsオブジェクトへの変換
ts_sim <- ts(df_sim$y, start = 1, frequency = 1)

cat("--- データ概要 ---\n")
cat(sprintf("総観測数: %d\n", n_obs))
cat(sprintf("真の構造変化点: %d 時点目\n", break_point))

--- データ概要 ---
総観測数: 100
真の構造変化点: 50 時点目

シミュレーションデータの可視化

# データの可視化
p1 <- ggplot(df_sim, aes(x = time, y = y)) +
  geom_line(color = "darkgrey") +
  geom_point(alpha = 0.6) +
  geom_vline(xintercept = break_point, linetype = "dashed", color = "red") +
  labs(
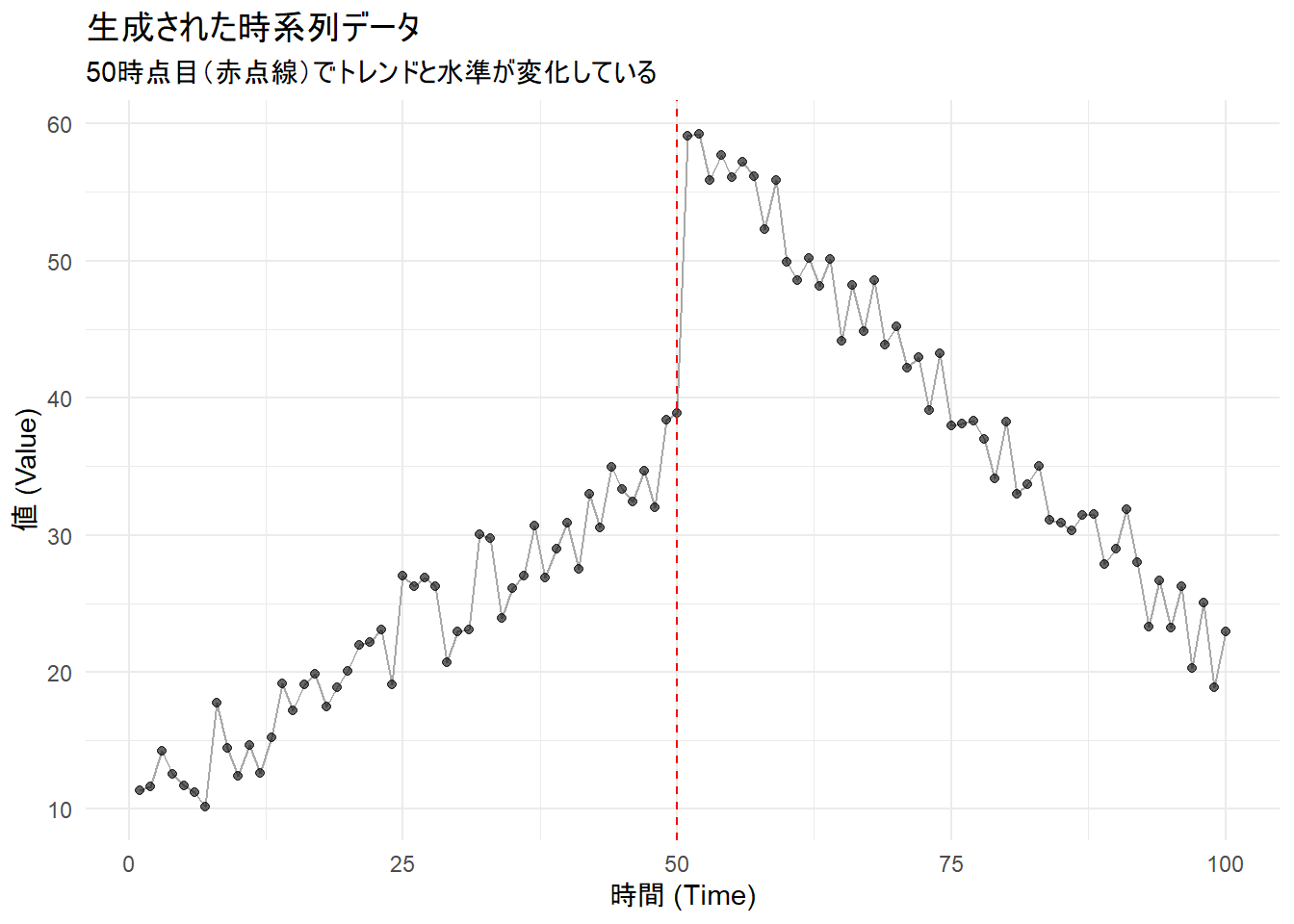
    title = "生成された時系列データ",
    subtitle = "50時点目（赤点線）でトレンドと水準が変化している",
    x = "時間 (Time)",
    y = "値 (Value)"
  ) +
  theme_minimal()

print(p1)

Fstats による構造変化の検出

Fstatsは、あらゆる時点を「分割点」と仮定してChow検定を行った結果の集合です。

F値が大きいほど、「その点でデータを分割した方がモデルの当てはまりが良い」、すなわち「構造変化が起きている可能性が高い」ことを示唆します。

# Fstats の実行
# y を 定数項と時間トレンド(time) で回帰し、係数の安定性を検定する
# from = 0.15 は、最初と最後の15%を除いた区間で検定を行うことを意味する
fs <- Fstats(y ~ time, data = df_sim, from = 0.15)

# F統計量の最大値を持つ時点（推定された変化点）を取得
estimated_break <- fs$breakpoint

cat(sprintf("推定された変化点 (Breakpoint): %d\n", estimated_break))
cat(sprintf("真の変化点                    : %d\n\n", break_point))

推定された変化点 (Breakpoint): 50
真の変化点                    : 50

F統計量の推移を可視化

# Fstatsの結果は、データフレーム入力時に時間が [0, 1] に正規化される仕様があるため、
# time() の値に観測数 (n_obs) を掛けて、元の時間軸 (1〜100) に戻します。
df_fstats <- data.frame(
  time = as.numeric(time(fs$Fstats)) * n_obs,
  F_value = as.numeric(fs$Fstats)
)

p2 <- ggplot(df_fstats, aes(x = time, y = F_value)) +
  geom_line(color = "blue", linewidth = 1) +
  geom_vline(xintercept = estimated_break, linetype = "dashed", color = "red") +
  labs(
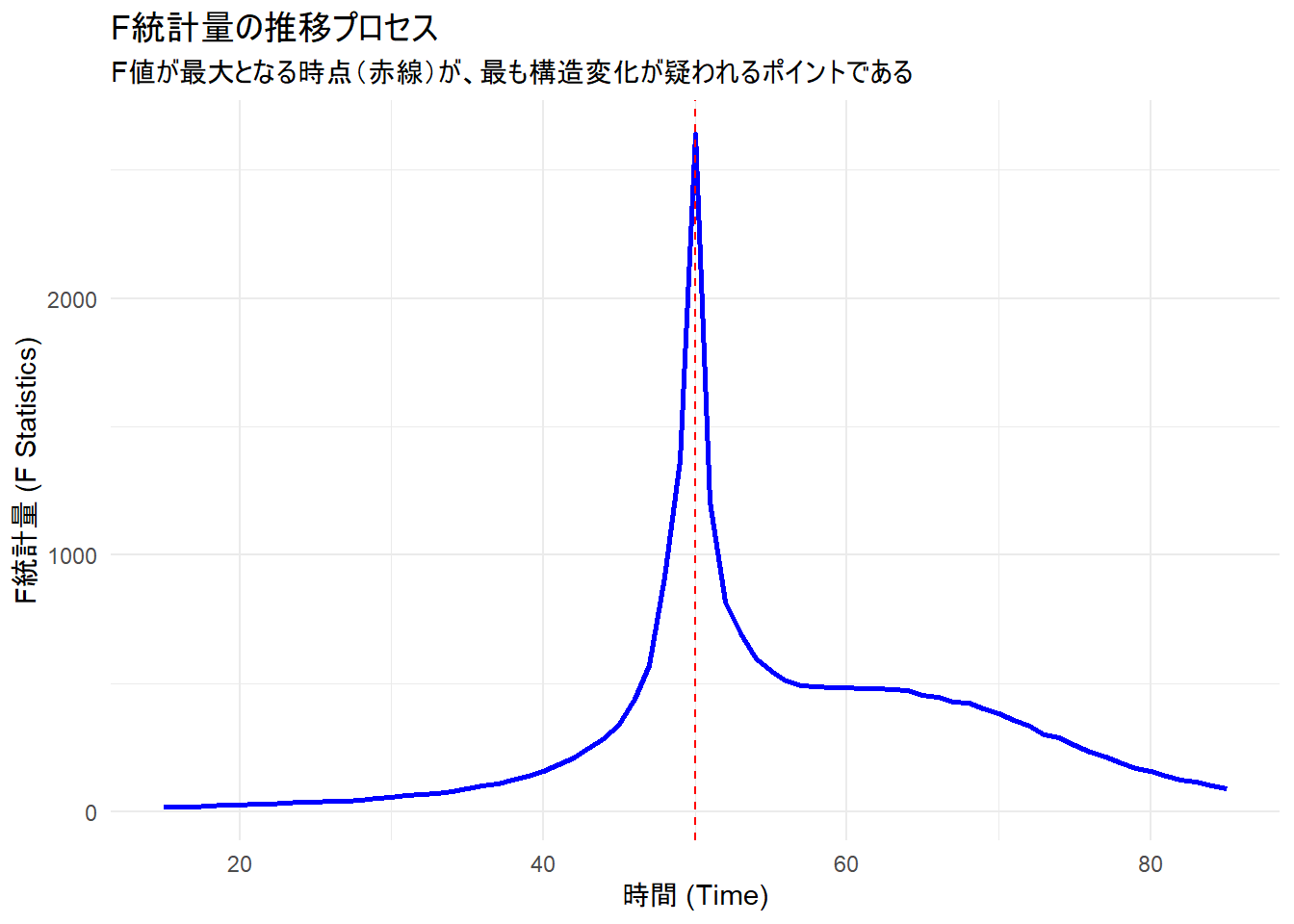
    title = "F統計量の推移プロセス",
    subtitle = "F値が最大となる時点（赤線）が、最も構造変化が疑われるポイントである",
    x = "時間 (Time)",
    y = "F統計量 (F Statistics)"
  ) +
  theme_minimal()

print(p2)

グラフの全体像：F統計量による「変化点」の探索

このグラフ（青い線）は、データの期間内のあらゆる時点を「ここが変化点かもしれない」と仮定して計算された、F統計量（モデル適合度の改善度合い）の推移を表しています。

横軸（Time）:
- 変化点の候補となる時間です。
縦軸（F Statistics）:
- 「その時点でデータを前後に分割した場合、モデルの当てはまりがどれだけ良くなるか」を示すスコアです。値が大きいほど、その前後でデータの性質が大きく異なっていることを意味します。

鋭いピーク（山）の意味

グラフの中央、時間50付近でF統計量が急激に上昇し、鋭いピーク（最大値2400以上）を形成しています。

シミュレーションデータの真の構造変化点は「50」です。この点でデータを分割すると、前半の「上昇トレンド」と後半の「下降トレンド」をきれいに分離でき、モデルの誤差（残差平方和）が最小になるため、F統計量は最大になります。

例えば時間40や60で分割しようとすると、片方のグループに「上昇トレンド」と「下降トレンド」のデータが混在してしまいます。その結果、モデルの当てはまりが悪くなり、F統計量は低下します。

赤い破線と結論

赤い破線は、F統計量が最大となった時点（推定された変化点）を示しています。

この線がピークの頂点を正確に貫いていることから、関数 Fstats が「時間50が最も構造変化の疑いが強い（最も尤もらしい変化点である）」と、真の変化点（50）と推定結果が一致しており、正しく特定できたことが分かります。

補足：グラフの両端の空白

グラフの横軸が約15から始まり、約85で終わっているのは、関数 Fstats の引数 from = 0.15（デフォルト）により、データの最初と最後の15%が検定対象から除外されているためです。

以上です。

関数 Fstats とは

関数 Fstats の引数