Rの関数:wilcox.test {stats}:ウィルコクソンの符号順位検定(対応あり2標本の場合)

# パッケージの読み込み
library(ggplot2)
library(tidyr)

# 乱数シードの固定
seed <- 20260125
set.seed(seed)

# 対応のある2標本ウィルコクソン符号順位検定のシミュレーション

# 1. サンプルデータの生成
# シナリオ: あるトレーニングの効果測定（事前 vs 事後）
n_pairs <- 20

# 事前データ (Pre): 平均60、標準偏差10の正規分布
pre_data <- rnorm(n_pairs, mean = 60, sd = 10)

# 真の効果 (Effect): 全体として +5.0 の上昇効果があるとする
true_effect <- 5.0

# 事後データ (Post): 事前データ + 真の効果 + 個体ごとのバラつき(ノイズ)
# 「対応あり」とは、PreとPostに相関があることを意味します。
post_data <- pre_data + true_effect + rnorm(n_pairs, mean = 0, sd = 2)

# データフレームの作成（可視化用）
df_paired <- data.frame(
  ID = factor(rep(1:n_pairs, 2)),
  Time = factor(rep(c("事前", "事後"), each = n_pairs), levels = c("事前", "事後")),
  Score = c(pre_data, post_data)
)

# データの可視化
# 「対応のあるデータ」の可視化には、箱ひげ図よりも
# 個体ごとの変化をつないだスロープチャート（Parallel Coordinate Plot）が適しています。
p1 <- ggplot(df_paired, aes(x = Time, y = Score)) +
  # 個体ごとの変化線
  geom_line(aes(group = ID), color = "gray60", alpha = 0.7) +
  # 点の描画
  geom_point(aes(color = Time), size = 3) +
  # 平均値の変化（赤線）
  stat_summary(
    fun = mean, geom = "line", aes(group = 1), color = "red",
    linewidth = 1.2, linetype = "dashed"
  ) +
  scale_color_manual(values = c("事前" = "blue", "事後" = "darkgreen")) +
  labs(
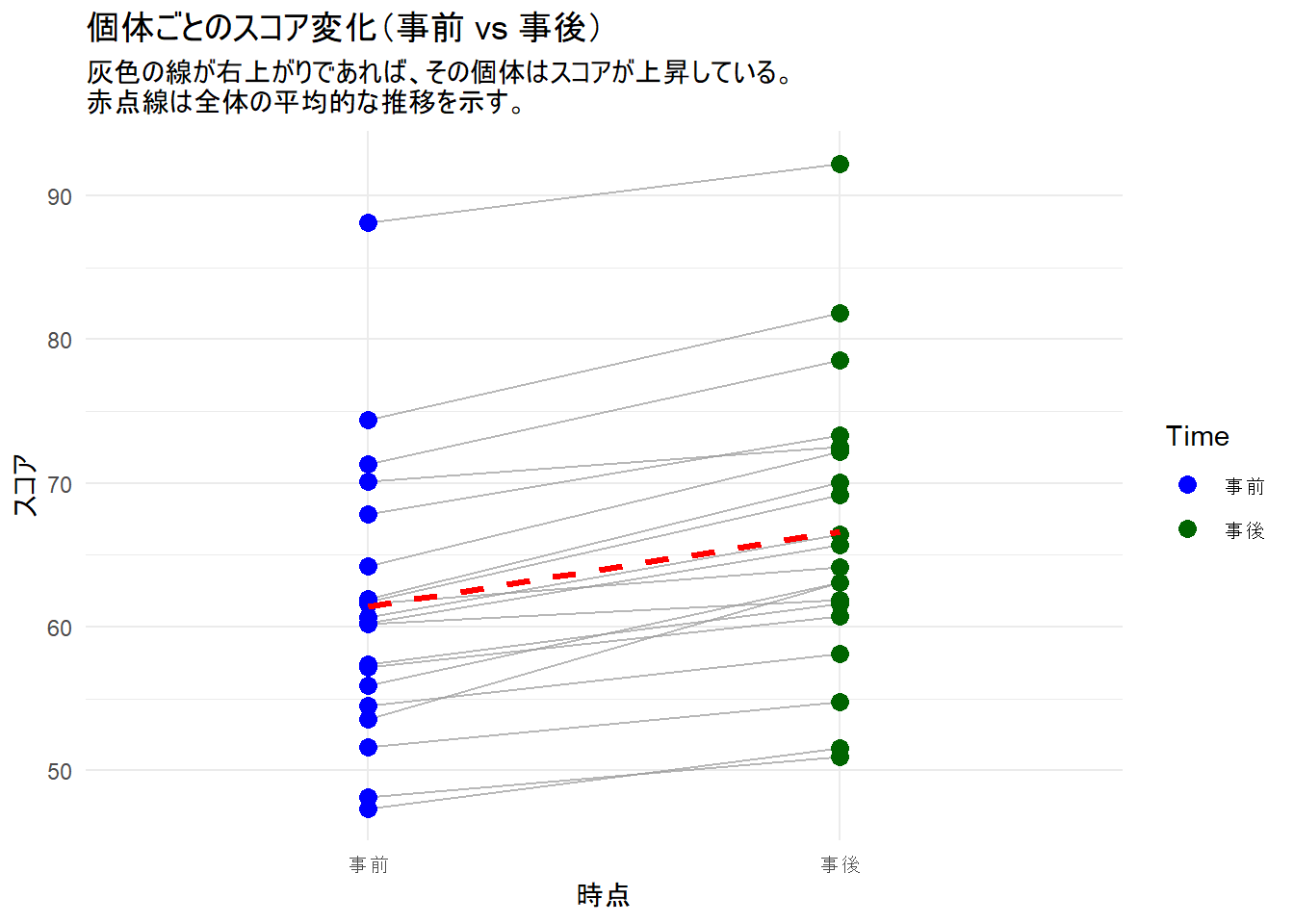
    title = "個体ごとのスコア変化（事前 vs 事後）",
    subtitle = "灰色の線が右上がりであれば、その個体はスコアが上昇している。\n赤点線は全体の平均的な推移を示す。",
    x = "時点",
    y = "スコア"
  ) +
  theme_minimal()

print(p1)

cat("--- データ概要 ---\n")
cat(sprintf("ペア数: %d 組\n", n_pairs))
cat(sprintf("真の上昇効果: +%.1f\n", true_effect))


# 2. 検定の実行
# paired = TRUE を指定することで、対応のある検定を実行します。
# 内部的には「差分 (x - y)」に対して1標本検定を行っているのと同義です。
test_res_paired <- wilcox.test(pre_data, post_data, paired = TRUE, conf.int = TRUE)

# 結果の表示
cat("\n--- 検定結果 ---")
print(test_res_paired)