Rの関数から wilcox.test {stats}:ウィルコクソンの順位和検定 / Wilcoxon Rank Sum Test を確認します。
本ポストはこちらの続きです。

ウィルコクソンの順位和検定 / Wilcoxon Rank Sum Test
何を検定している関数か
Rank Sum Test における wilcox.test の帰無仮説は次の通りです。
\[H_0:\ X \stackrel{d}{=} Y + \mu\]
すなわち、2 群は同一形状の分布で、違いがあるとすれば位置(平行移動)だけ という 位置シフトモデルを仮定しています。
「中央値差検定」と呼べる条件
Rank Sum Test を 「2 群の中央値差の検定」と呼べるのは、
- 両群が 同一形状の連続分布
- 違いは位置のみ
という条件が成立している場合に限られます。
コードの主要なロジック
wilcox.test における「Wilcoxon Rank Sum Test(対応のない2標本検定)」は、マン・ホイットニーのU検定と実質的に同一のアルゴリズムで構成されています。
データの統合と順位付け(Ranking)
まず、比較対象となる2つの群(標本 \(x\) と標本 \(y\))を一つのベクトルに統合いたします。
位置パラメータの差(mu)が指定されている場合は、標本 \(x\) からその値を差し引いた上で統合処理を行います。
その後、統合された全データに対して昇順で順位(Rank)を付与いたします。
同順位(タイ)が存在する場合、rank 関数はそれらの平均順位を割り当てます。
検定統計量 \(W\) の算出
次に、標本 \(x\) に割り当てられた順位の合計(順位和)を算出いたします。
\(U\) 統計量を得るために、算出した順位和から標本 \(x\) のサイズ \(n_x\) に基づく最小値 \(n_x(n_x + 1)/2\) を減じます。
\[W = \sum R_x - \frac{n_x(n_x + 1)}{2}\]
計算によって得られる \(W\) は、標本 \(y\) の各要素よりも値が大きい標本 \(x\) の要素の組合わせの数に等しくなります。
検定手法の判定(Exact vs. Asymptotic)
計算された統計量の有意性を判定するにあたり、「正確な確率(Exact p-value)」を求めるか、あるいは「正規近似(Normal Approximation)」を用いるかを選択いたします。
- 正確な検定:
- 両群のサンプルサイズが50未満であり、かつデータ内に同順位(タイ)が存在しない場合、この手法が優先されます。
- 正規近似:
- サンプルサイズが50以上であるか、あるいはデータ内に同順位が含まれる場合、中心極限定理に基づく近似計算が採用されます。
確率(p値)の計算実行
選択された手法に基づき、帰無仮説下での \(p\) 値を算出いたします。
- 正確な計算の場合:
- 離散的な確率分布である
pwilcox関数(Wilcoxon順位和分布)を用います。対立仮説が「両側(two.sided)」であれば、期待値(\(n_x n_y / 2\))との乖離に基づき確率を2倍にする処理が行われます。
- 離散的な確率分布である
- 正規近似の場合:
- 統計量 \(W\) の期待値と分散を用いて \(z\) 統計量を算出いたします。
検定ロジックに特化した簡略化関数
以下は、入力チェックや信頼区間の計算を省き、検定統計量 \(W\) と \(p\) 値を算出することに特化した関数 simple_wilcox_rank_sum です。
ウィルコクソンの順位和検定は、マン・ホイットニーのU検定(Mann-Whitney U test)と同等であり、対応のない2群間の位置の差を評価いたします。
# Wilcoxon Rank Sum Test(対応のない2標本検定)の簡略化関数
simple_wilcox_rank_sum <- function(x, y, mu = 0, alternative = "two.sided", exact = NULL, correct = TRUE) {
# 1. サンプルサイズの取得
n.x <- as.double(length(x))
n.y <- as.double(length(y))
# 2. 順位付けの実行
# 両群を統合し、xから位置パラメータ(mu)を引いた状態で全体の順位を算出する
r <- rank(c(x - mu, y))
# 3. 検定統計量 W の算出
# xの順位和から、xのサイズに基づいた定数を差し引く
statistic <- sum(r[seq_along(x)]) - n.x * (n.x + 1) / 2
# 4. タイ(同順位)の判定
ties <- (length(r) != length(unique(r)))
if (is.null(exact)) {
exact <- (n.x < 50) && (n.y < 50)
}
# 5. p値の計算
if (exact && !ties) {
# --- 正確な検定(タイがない場合) ---
p_val <- switch(alternative,
two.sided = {
p <- if (statistic > (n.x * n.y / 2)) {
pwilcox(statistic - 1, n.x, n.y, lower.tail = FALSE)
} else {
pwilcox(statistic, n.x, n.y)
}
min(2 * p, 1)
},
greater = pwilcox(statistic - 1, n.x, n.y, lower.tail = FALSE),
less = pwilcox(statistic, n.x, n.y)
)
} else {
# --- 正規近似(タイがある、またはサンプルサイズが大きい場合) ---
nties <- table(r)
z <- statistic - n.x * n.y / 2
# タイを考慮した標準偏差(SIGMA)の算出
# 分母の補正を含め、元の実装を再現している
sigma <- sqrt((n.x * n.y / 12) * ((n.x + n.y + 1) -
sum(nties^3 - nties) / ((n.x + n.y) * (n.x + n.y - 1))))
# 連続性の補正
correction <- 0
if (correct) {
correction <- switch(alternative,
two.sided = sign(z) * 0.5,
greater = 0.5,
less = -0.5
)
}
z_stat <- (z - correction) / sigma
p_val <- switch(alternative,
less = pnorm(z_stat),
greater = pnorm(z_stat, lower.tail = FALSE),
two.sided = 2 * min(pnorm(z_stat), pnorm(z_stat, lower.tail = FALSE))
)
}
# 統計量とp値をリスト形式で返却する
return(list(statistic = c(W = statistic), p.value = as.numeric(p_val)))
}シミュレーションコード
「正規分布に従わない(歪みのある)独立した2つの集団」を生成し、平均値の差ではなく、分布の位置(順位)に差があるかを検定する、対応のない2標本ウィルコクソン順位和検定 です。
なお、有意水準は5%とします。
# パッケージの読み込み
library(ggplot2)
library(dplyr)
# 乱数シードの固定
seed <- 20260126
set.seed(seed)
# 対応のない2標本ウィルコクソン順位和検定のシミュレーション
# 1. サンプルデータの生成
# シナリオ: 2つの異なるウェブサイトデザイン(A案、B案)における滞在時間の比較
# 滞在時間は、左側にピークがあり右に裾を引く「ガンマ分布」や「対数正規分布」に従うと仮定します。
# グループA (既存デザイン): n=40
n_a <- 40
# ガンマ分布 (shape=2, scale=10) -> 平均20秒程度、右に歪んだ分布
data_a <- rgamma(n_a, shape = 2, scale = 10)
# グループB (新デザイン): n=50 (サンプルサイズが異なっていても構いません)
n_b <- 50
# グループAよりも全体的に滞在時間が長い(位置が右にズレている)
# 真のズレ (Location Shift) を +15秒 とする
true_shift <- 15.0
data_b <- rgamma(n_b, shape = 2, scale = 10) + true_shift
# データフレームの作成
df_unpaired <- data.frame(
Value = c(data_a, data_b),
Group = factor(c(rep("デザインA", n_a), rep("デザインB", n_b)))
)
# データの可視化
# 密度プロット(Density Plot)で分布の形状とズレを確認します
p1 <- ggplot(df_unpaired, aes(x = Value, fill = Group)) +
geom_density(alpha = 0.5) +
geom_vline(aes(xintercept = median(data_a), color = "デザインA中央値"),
linetype = "dashed", linewidth = 1
) +
geom_vline(aes(xintercept = median(data_b), color = "デザインB中央値"),
linetype = "dashed", linewidth = 1
) +
scale_color_manual(
name = "指標",
values = c("デザインA中央値" = "darkblue", "デザインB中央値" = "darkred")
) +
scale_fill_manual(values = c("デザインA" = "blue", "デザインB" = "red")) +
labs(
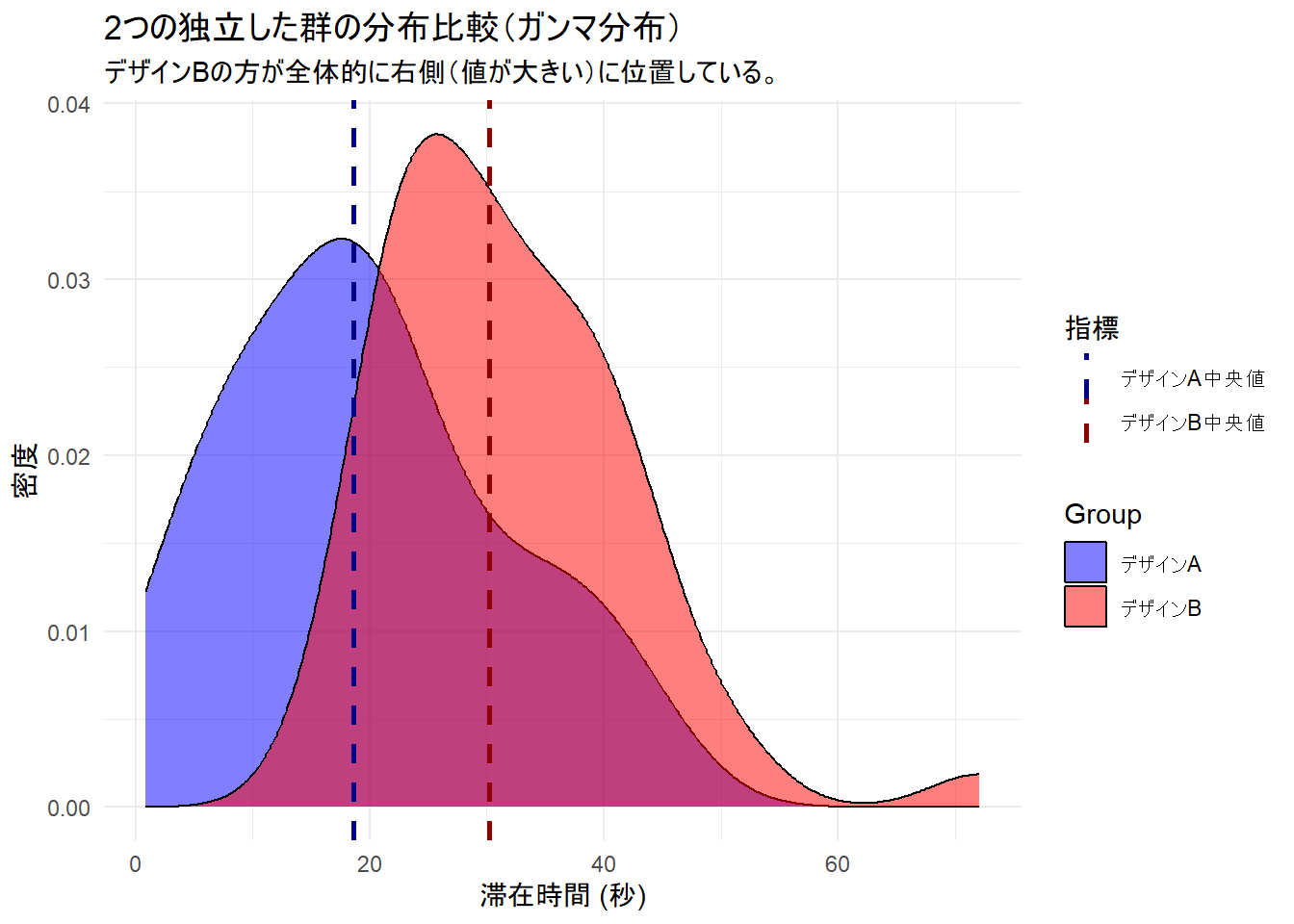
title = "2つの独立した群の分布比較(ガンマ分布)",
subtitle = "デザインBの方が全体的に右側(値が大きい)に位置している。",
x = "滞在時間 (秒)",
y = "密度"
) +
theme_minimal()
print(p1)
cat("--- データ概要 ---\n")
cat(sprintf("デザインA: n=%d, 中央値=%.2f\n", n_a, median(data_a)))
cat(sprintf("デザインB: n=%d, 中央値=%.2f\n", n_b, median(data_b)))
cat(sprintf("設定した真のズレ: +%.1f\n\n", true_shift))
# 2. 検定の実行
# paired = FALSE (デフォルト) を指定、または省略することで順位和検定が実行されます。
# alternative = "two.sided" (両側検定)
# conf.int = TRUE (位置の差の信頼区間を計算)
test_res_unpaired <- wilcox.test(data_a, data_b, paired = FALSE, conf.int = TRUE)
# 結果の表示
cat("\n--- 検定結果要 ---")
print(test_res_unpaired)--- データ概要 ---
デザインA: n=40, 中央値=18.57
デザインB: n=50, 中央値=30.22
設定した真のズレ: +15.0
--- 検定結果要 ---
Wilcoxon rank sum test with continuity correction
data: data_a and data_b
W = 427, p-value = 3.341e-06
alternative hypothesis: true location shift is not equal to 0
95 percent confidence interval:
-16.654278 -7.448982
sample estimates:
difference in location
-12.14563 検定の結論 (P値による判定)
P値は 約 0.0000033 と(p-value = 3.341e-06)、設定した有意水準を下回っており、「2つの分布の位置に差はない」という帰無仮説は棄却されます。
位置の推定 (Difference in location)
位置の差の推定値(ホッジス・レーマン推定量)は 約 -12.15 です(difference in location : -12.14563)。
- 符号の意味:
- マイナスになっているのは、関数が「
data_a-data_b」の方向で差を評価しているためです。「AはBより約12小さい」=「BはAより約12大きい」ことを意味します。
- マイナスになっているのは、関数が「
- 設定との整合性:
- シミュレーションでは、BをAより +15.0 大きく設定しました(つまり A - B = -15.0)。推定値(-12.15)は、乱数によるバラつきを含みつつも、この真のズレの方向と大きさを捉えています。
95%信頼区間
位置の差の95%信頼区間は [-16.65, -7.45] と(95 percent confidence interval: -16.654278 -7.448982)、区間全体が負の領域にあり、0を含んでいません。
統計量 W と連続性の補正
- W = 427:
- これはマン・ホイットニーのU統計量に相当します。サンプルサイズ(\(40 \times 50 = 2000\))に対して値が小さいことは、
data_aの順位が全体的に低い(値が小さい)ことを示唆しています。
- これはマン・ホイットニーのU統計量に相当します。サンプルサイズ(\(40 \times 50 = 2000\))に対して値が小さいことは、
- Continuity correction:
- 今回はサンプルサイズが比較的大きく、同順位(タイ)が含まれる可能性があるデータ分布(ガンマ分布)を用いたため、離散的な順位データを連続分布(正規分布)で近似する際の精度を高めるために、「連続性の補正」が行われています(Wilcoxon rank sum test with continuity correction)。
簡略化関数による結果
simple_wilcox_rank_sum(x = data_a, y = data_b)$statistic
W
427
$p.value
[1] 3.340527e-06統計量とp値は一致しています。
以上です。