Rの関数:aov {stats}

Rの関数から aov {stats} を確認します。

関数 `aov` とは

aov 関数は、分散分析（Analysis of Variance: ANOVA）モデルを適合させるための関数です。

aov は lm のラッパー（機能を包含し、特定の用途向けに調整したもの）として設計されています。

当該関数により、実験計画法における「誤差項の層化（Error Strata）」を扱うことができます。

具体的には、通常の線形回帰モデルに加え、分割実験（Split-plot design）や反復測定（Repeated measures）デザインのような、複数の誤差構造を持つモデルを Error()項を用いて指定することが可能です。

Error()項が含まれる場合、aov はデータを直交する層（Stratum）に射影し、各層ごとにモデルを適合させます。

出力されるオブジェクトは、単一のモデルの場合は aov クラス（lm クラスを継承）、Error()項を含む場合は aovlist クラスとなります。

関数 `aov` の引数

formula
- モデルの構造を指定する式です。形式は response ~ terms となります。
- Error(strata) という形式で誤差構造を指定できます。例えば、被験者内要因を持つデザインでは response ~ factorA * factorB + Error(Subject/factorA) のように記述し、変量効果としての誤差層を定義します。
data
- formula 内の変数が含まれているデータフレームまたはリストです。
- デフォルト: NULL（この場合、環境内の変数が参照されます）。
projections
- 適合値の射影（projections）を返すかどうかの論理値です。
- デフォルト: FALSE。
- TRUE の場合、各項に対する適合値の成分が返されます。各要因が応答変数にどの程度寄与しているかを確認する際に有用です。
qr
- QR分解の結果を返すかどうかの論理値です。
- デフォルト: TRUE。
contrasts
- 因子（factor）変数の対比（contrasts）を指定するリストです。
- デフォルト: NULL。
- aov は Error()項を持つモデルを適合させる際、デフォルトで contr.helmert（ヘルマート対比）および contr.poly（直交多項式対比）を使用するように設定を変更します。特定の対比を指定したい場合、この引数を使用します。
...
- lm 関数等の内部関数へ渡されるその他の引数です。
- 例: subset（データの部分集合を指定）や na.action（欠損値の扱いを指定）などが含まれます。

シミュレーションコード

以下に、aov の機能を確認するためのサンプルデータを用いたシミュレーションコードを示します。

このシミュレーションでは、単純な一元配置分散分析ではなく、aov の機能を利用するために「分割実験（Split-Plot Design）」を想定したデータを生成します。

シナリオ:

ある製パン工場における「パンのふくらみ（Volume）」に対する実験を想定します。

第1因子（全体区）:
- オーブンの種類（Oven: A, B）。
第2因子（細区）:
- 小麦粉の種類（Flour: X, Y, Z）。同じオーブンの中で、異なる小麦粉の生地を焼くことができます。
ブロック:
- 実験を行う「日（Day）」をブロック因子とします。

このデータ構造には、オーブン由来の誤差（全体区誤差）と、小麦粉および相互作用由来の誤差（細区誤差）の2つの層が存在します。通常の lm ではこの誤差構造を正しく扱うことが困難ですので、aov の Error() 項を用います。

なお、有意水準は5%とします。

分割実験（Split-Plot Design）データの生成

データ概要:

実験単位 : 製パン実験
目的変数 : Volume (パンのふくらみ)
要因1 (Whole-plot) : Oven (A, B)
要因2 (Sub-plot) : Flour (X, Y, Z)
ブロック : Day (1~6)

# パッケージの読み込み
library(ggplot2)
library(dplyr)

# 乱数シードの固定
seed <- 20260129
set.seed(seed)

# 設定:
# 6日間 (Day: Block)
# 2種類のオーブン (Oven: Whole-plot factor)
# 3種類の小麦粉 (Flour: Sub-plot factor)
n_days <- 6
levels_oven <- c("Oven_A", "Oven_B")
levels_flour <- c("Flour_X", "Flour_Y", "Flour_Z")

# データの骨組み作成
# 各日において、あるオーブンが割り当てられ（実際はランダム化されるがここでは簡略化）、
# その中で3種類の小麦粉をテストする構造
df_sim <- expand.grid(
  Day = factor(1:n_days),
  Oven = factor(levels_oven),
  Flour = factor(levels_flour)
)

# 実験計画的な制約: 分割実験では「日×オーブン」が全体区（Whole Plot）となる
# ここではバランス良くデータを生成するため、全組み合わせを使用します。
# データ数: 6 * 2 * 3 = 36 観測

# 真の効果の設定
base_volume <- 300 # 基準のふくらみ
eff_oven_b <- 20 # オーブンBの効果 (+20)
eff_flour_y <- -10 # 小麦粉Yの効果 (-10)
eff_flour_z <- 30 # 小麦粉Zの効果 (+30)
eff_inter_b_z <- 15 # オーブンBかつ小麦粉Zの時の相互作用効果 (+15)

# 変量効果（誤差項）の生成
# 1. ブロック（日）による変動
error_day <- rnorm(n_days, mean = 0, sd = 5)
names(error_day) <- 1:n_days

# 2. 全体区誤差（日×オーブンの組み合わせごとの誤差）: Error(Day:Oven)
# オーブンの温度ムラなどに相当
n_whole_plots <- n_days * length(levels_oven)
error_whole <- rnorm(n_whole_plots, mean = 0, sd = 8)

# 3. 残差（測定ごとの誤差）
n_obs <- nrow(df_sim)
error_resid <- rnorm(n_obs, mean = 0, sd = 3)

# データの構築
df_sim$Volume <- base_volume +
  # 固定効果
  ifelse(df_sim$Oven == "Oven_B", eff_oven_b, 0) +
  ifelse(df_sim$Flour == "Flour_Y", eff_flour_y, 0) +
  ifelse(df_sim$Flour == "Flour_Z", eff_flour_z, 0) +
  ifelse(df_sim$Oven == "Oven_B" & df_sim$Flour == "Flour_Z", eff_inter_b_z, 0) +
  # 変量効果
  error_day[df_sim$Day] +
  error_whole[as.numeric(interaction(df_sim$Day, df_sim$Oven))] +
  error_resid

# データの可視化
# オーブンごと、小麦粉ごとのふくらみの違いを図示
p1 <- ggplot(df_sim, aes(x = Flour, y = Volume, fill = Oven)) +
  geom_boxplot(alpha = 0.7) +
  geom_jitter(position = position_jitterdodge(), alpha = 0.5) +
  labs(
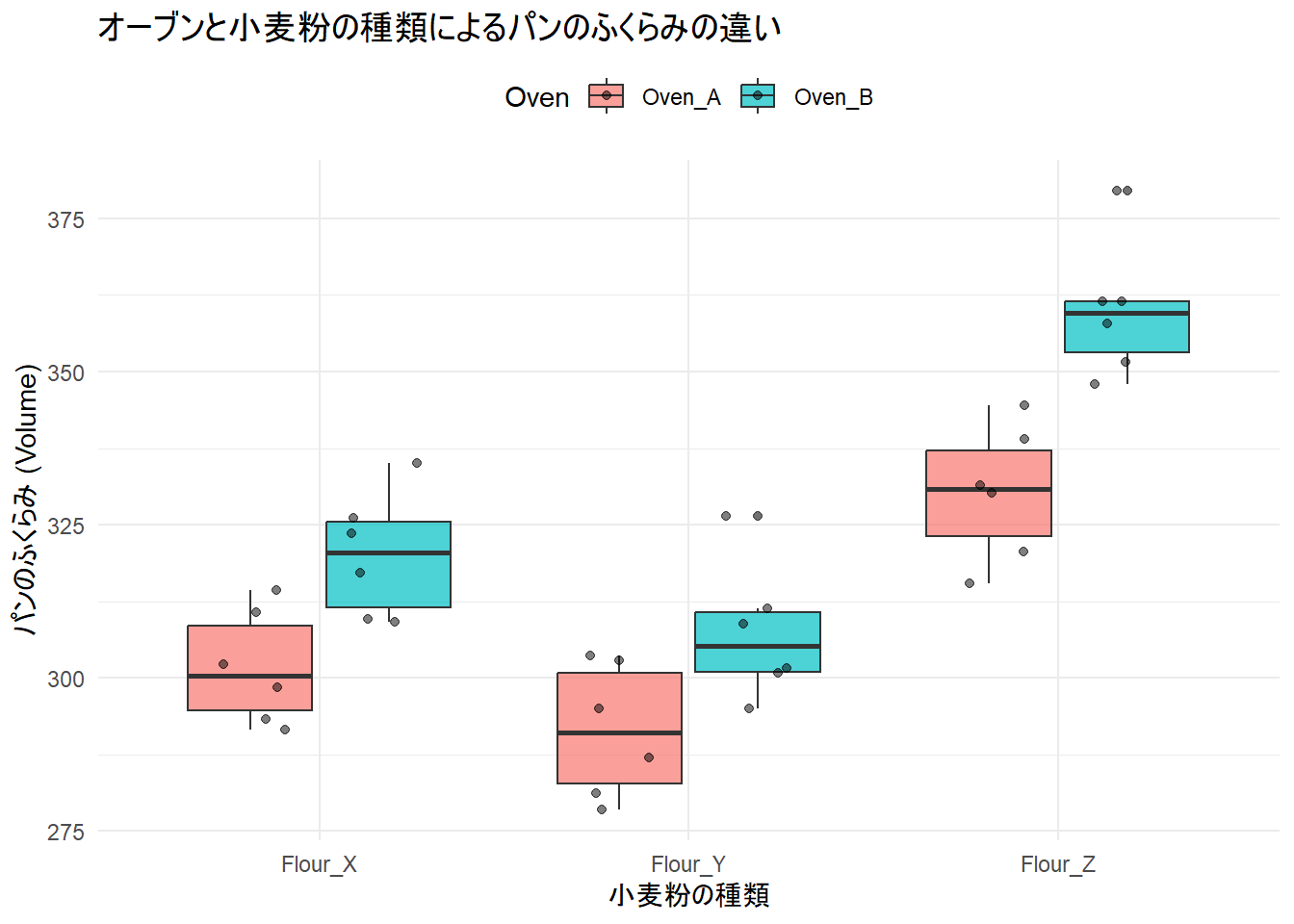
    title = "オーブンと小麦粉の種類によるパンのふくらみの違い",
    x = "小麦粉の種類",
    y = "パンのふくらみ (Volume)"
  ) +
  theme_minimal() +
  theme(legend.position = "top")

print(p1)

Figure 1 には設定通り、オーブンBかつ小麦粉Zの場合に特異的な上昇（相互作用）が見られます。

解析1: 誤った解析 (誤差構造を無視)

すべての誤差を「一緒くた」にした通常の分散分析です。

# Error項を指定しない通常のANOVA
model_wrong <- aov(Volume ~ Oven * Flour, data = df_sim)
print(summary(model_wrong))

            Df Sum Sq Mean Sq F value   Pr(>F)    
Oven         1   4108    4108  37.104 1.08e-06 ***
Flour        2  13570    6785  61.287 2.54e-11 ***
Oven:Flour   2    327     164   1.477    0.244    
Residuals   30   3321     111                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

表の読み方と判定結果

Oven (オーブン):
- P値 (1.08e-06) が設定した有意水準を下回っていますので、「オーブンの違いによる効果はない」との帰無仮説は棄却されます。
Flour (小麦粉):
- P値 (2.54e-11) が設定した有意水準を下回っていますので、「小麦粉の種類による効果はない」との帰無仮説も棄却されます。
Oven:Flour (相互作用):
- P値 (0.244) が設定した有意水準を上回っており、シミュレーションデータには、「オーブンBで小麦粉Zのときだけ特異的に膨らむ（+15）」という相互作用を組み込んでいたにも関わらず、「相互作用なし」との帰無仮説を棄却できません。

なぜ「誤った解析」なのか？

一番下の行、Residuals（残差） を確認します。

Mean Sq (平均平方): 111

この 111 という数値は、このモデルにおける「誤差の大きさ（分散）」を表し、すべてのF値計算の分母（割り算の底）として使われています。

本来の残差誤差:
- 設定では SD=3 なので、分散は \(3^2 = 9\) 程度のはずです。
なぜ 111 になったか:
- 誤差構造を無視したため、本来分離すべき「大きな誤差（オーブンのムラ：SD=8 \(\to\) 分散64）」や「日の変動」が、すべてここに混ざり込んでしまったからです。

解析の失敗メカニズム

この「大きすぎる誤差（111）」を基準（分母）にしてF値を計算したため、本来の実験精度（分散9）で検定すれば検出できたはずの「相互作用の効果」が、ノイズまみれの基準（分散111）と比較されたことで、「誤差の範囲内」と誤って判断されてしまいました（タイプIIエラー）。

解析2: 正しい解析 (Error項を使用)

分割実験のデザインを反映し、誤差項を層化します。
式: Volume ~ Oven * Flour + Error(Day/Oven)
Dayの中にOvenという単位があり、それが全体区誤差となることを指定しています。

# Error項を指定したANOVA
# DayごとのOvenのばらつきを誤差として指定
model_correct <- aov(Volume ~ Oven * Flour + Error(Day / Oven), data = df_sim)

print(summary(model_correct))


Error: Day
          Df Sum Sq Mean Sq F value Pr(>F)
Residuals  5  300.3   60.05               

Error: Day:Oven
          Df Sum Sq Mean Sq F value Pr(>F)  
Oven       1   4108    4108   7.129 0.0443 *
Residuals  5   2881     576                 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Error: Within
           Df Sum Sq Mean Sq F value   Pr(>F)    
Flour       2  13570    6785  967.94  < 2e-16 ***
Oven:Flour  2    327     164   23.33 5.91e-06 ***
Residuals  20    140       7                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

`Error: Within` （細区：Sub-plot）

小麦粉（Flour）や相互作用を検定する層です。

Residuals の Mean Sq（平均平方）: 7
- 「誤った解析」では 111 でした。
- 正しい解析を行うことで、オーブンや日による大きなノイズが取り除かれ、真の測定誤差（設定したSD=3の2乗に近い値）だけが抽出されました。
- ノイズ（分母）が 111 から 7 へと 約1/16 に縮小しました。
Oven:Flour（相互作用）の判定:
- F値: 1.477 \(\to\) 23.33 （上昇）
- P値: 0.244（棄却できず） \(\to\) 5.91e-06（棄却）
- 結論: ノイズが除去されたことで、本来そこにあった「オーブンと小麦粉の相互作用」を検出できました。

`Error: Day:Oven` （全体区：Whole-plot）

オーブン（Oven）の効果を検定する層です。

Residuals の Mean Sq: 576
- 「誤った解析」の 111 よりも逆に大きくなっています。
- これは、「オーブンの差を語るなら、オーブンごとの温度ムラ（全体区誤差。設定ではSD=8 \(\to\) 分散64）などの大きな変動を基準に評価すべきだ」という正しい基準が適用されたためです。
Oven の判定:
- P値: 1.08e-06 \(\to\) 0.0443
- 過大評価の抑制方向にP値が大きくなり、判定が厳しくなりました。

分散分析において、統計的有意性を決める「F値」は、以下の割り算で求められます。
\[ F値 = \frac{\text{効果の大きさ (OvenのMean Sq)}}{\text{誤差の大きさ (ResidualsのMean Sq)}} \]
今回の Error: Day:Oven 層の数値で計算してみます。
分子（Ovenの効果）: 4108
分母（誤差の大きさ）: 576
\[ F = \frac{4108}{576} \approx 7.1 \]
誤った解析では以下の通り、F値が大きくなります。
分子: 4108
分母: 111 （誤った解析の値）
\[ F = \frac{4108}{111} \approx 37.0 \]
よって、「誤差に比べて効果が圧倒的に大きい」誤った解析よりも、「誤差に比べて効果はそこそこ大きい」正しい解析のP値は大きくなっています。

なぜ結果が変わったのか

aov 関数はデータを「3つの層」に分解しました。

Day層:
- 日ごとの変動（=関係ないノイズ）を吸収して捨てた。
Day:Oven層:
- オーブン単位の大きな変動を集め、Ovenの検定に使った（=基準を厳しくした）。
Within層:
- 純粋な測定ごとの変動を集め、Flourと相互作用の検定に使った（=基準を鋭敏にした）。

この分解により、「相互作用を見逃す（タイプIIエラー）」リスクと、「主効果を過大評価する（タイプIエラー）」リスクの両方を回避できたことがわかります。

以上です。

関数 aov とは

関数 aov の引数