Rの関数:ARMAtoMA {stats}

# パッケージの読み込み
library(ggplot2)

# 1. ARMAモデルのパラメータ設定
# モデル: X_t = 0.7 * X_{t-1} - 0.2 * X_{t-2} + Z_t + 0.5 * Z_{t-1}
# AR(2) + MA(1) = ARMA(2, 1) モデル
ar_coef <- c(0.7, -0.2)
ma_coef <- c(0.5)
max_lag <- 15

cat("--- モデル設定 ---\n")
cat(sprintf("AR係数 (phi)  : %s\n", paste(ar_coef, collapse = ", ")))
cat(sprintf("MA係数 (theta): %s\n", paste(ma_coef, collapse = ", ")))
cat(sprintf("計算ラグ数    : %d\n\n", max_lag))


# 2. ARMAtoMA を用いた係数計算
# これが理論的なインパルス応答係数（ラグ1～15）です
psi_weights <- ARMAtoMA(ar = ar_coef, ma = ma_coef, lag.max = max_lag)

cat("--- ARMAtoMAによる計算結果 (先頭5つを表示) ---\n")
print(head(psi_weights, 5))
cat("\n")


# 3. フィルタ関数を用いたシミュレーションによる検証
# インパルスデータの作成
# 時点1に「1」のインパルスを与え、その後は「0」が続くデータ
impulse_input <- c(1, rep(0, max_lag))

# 手順A: まずMA部分を適用 (Z_t + 0.5 * Z_{t-1})
# filter関数のsides=1は片側（過去のみ参照）フィルタを意味します
ma_filtered <- stats::filter(impulse_input,
  filter = c(1, ma_coef),
  method = "convolution", sides = 1
)
# NAを除去（最初の部分は計算できないためNAになりますが、ここでは先頭を補正）
# filterの挙動として、先頭の1はそのままで、次の項からMA係数が乗ります
# MA(1)なので、入力が(1,0,0...)なら、出力は(1, 0.5, 0...)となるはずです
# method="recursive"を使うARフィルタに入力する前の「MA変換済み入力」を作ります
ma_impulse <- c(1, ma_coef, rep(0, max_lag - length(ma_coef)))

# 手順B: 次にAR部分を適用 (再帰的フィルタ)
# これにより、無限に続く応答が生成されます
simulated_response <- stats::filter(ma_impulse,
  filter = ar_coef,
  method = "recursive"
)

# simulated_response の先頭はラグ0（値は1）なので、
# ARMAtoMAの結果（ラグ1以降）と比較するために2番目以降を取り出します
simulated_psi <- as.numeric(simulated_response)[2:(max_lag + 1)]

# 4. 結果の比較
df_compare <- data.frame(
  Lag = 1:max_lag,
  ARMAtoMA_Value = psi_weights,
  Simulated_Value = simulated_psi
)

cat("--- シミュレーション（フィルタ）結果との比較 (先頭5つを表示) ---\n")
print(head(df_compare, 5))
cat("\n係数は全て一致しているか : ", all.equal(target = df_compare$ARMAtoMA_Value, current = df_compare$Simulated_Value))

# 5. 可視化
# インパルス応答関数のプロット
p1 <- ggplot(df_compare, aes(x = Lag)) +
  # ゼロライン
  geom_hline(yintercept = 0, color = "gray50") +

  # ARMAtoMAの結果（赤い線と点）
  geom_line(aes(y = ARMAtoMA_Value, color = "ARMAtoMA (理論値)"),
    linewidth = 1
  ) +
  geom_point(aes(y = ARMAtoMA_Value, color = "ARMAtoMA (理論値)"),
    size = 3
  ) +

  # シミュレーション結果（青い×印）を重ねて表示
  geom_point(aes(y = Simulated_Value, color = "フィルタシミュレーション"),
    shape = 4, size = 5, stroke = 1.5
  ) +

  # 色の設定
  scale_color_manual(
    name = "",
    values = c(
      "ARMAtoMA (理論値)" = "firebrick",
      "フィルタシミュレーション" = "blue"
    )
  ) +

  # ラベル設定
  labs(
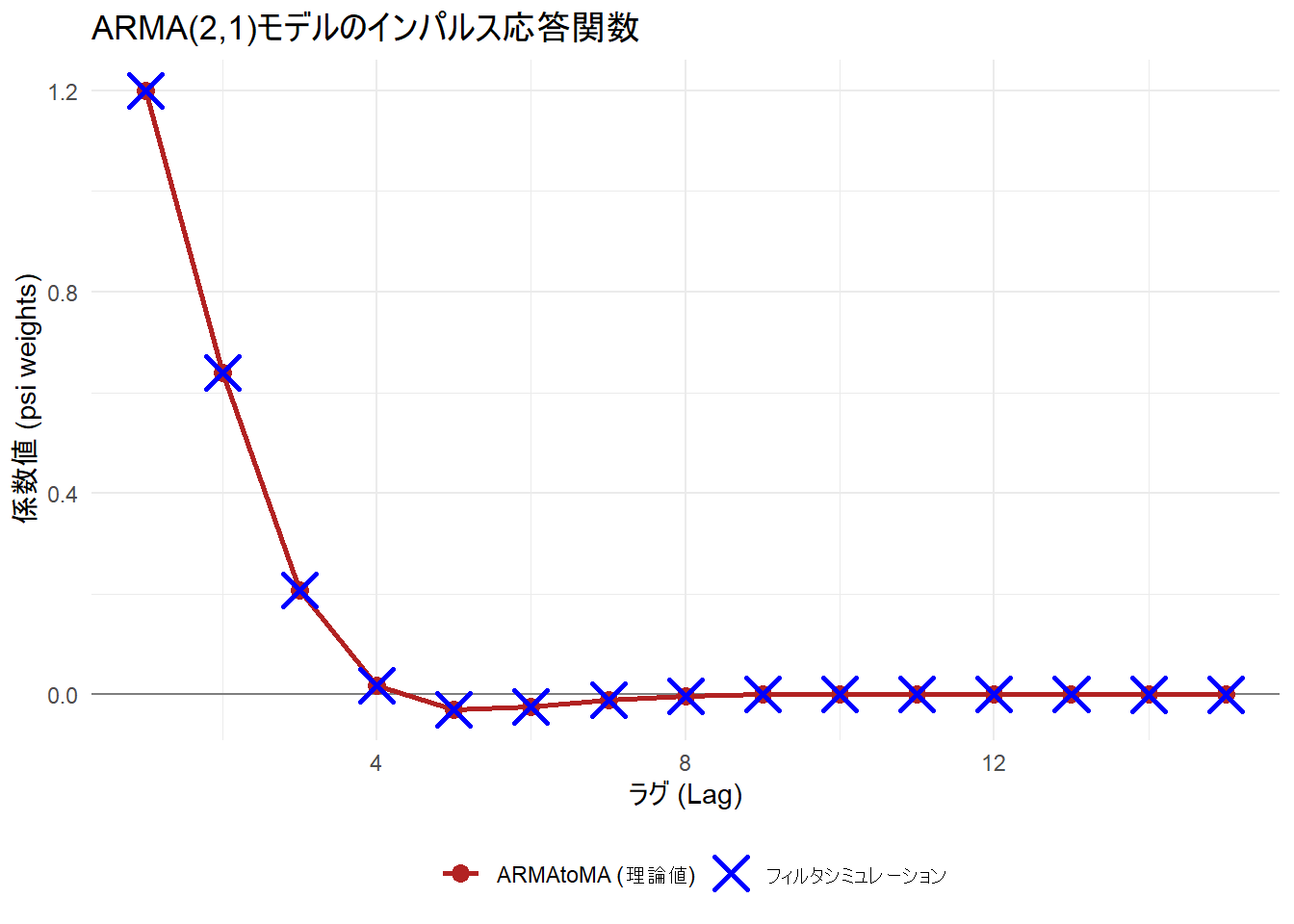
    title = "ARMA(2,1)モデルのインパルス応答関数",
    x = "ラグ (Lag)",
    y = "係数値 (psi weights)"
  ) +
  theme_minimal() +
  theme(legend.position = "bottom")

print(p1)