Rの関数から battleship.plot {plotrix} を確認します。
関数 battleship.plot とは
battleship.plot は、2次元行列の各要素の数値を、グリッド上に並んだ矩形(長方形)の「幅」として視覚化する関数です。
本関数は、行列内の最大値を基準として各要素を正規化し、数値が大きいほど横幅が広く、数値が小さいほど横幅が狭い矩形を描画します。
矩形の高さは一定に保たれるため、各行・各列における相対的な頻度や強度の変化を、グリッド状のレイアウトで直感的に把握できる点が特徴です。
内部処理では、staxlab 関数を用いて列ラベルを上部に斜め配置し、行ラベルを左側に配置することで、ラベル同士の重なりを防ぎつつ視認性を確保しています。
関数 battleship.plot の活用シーン
- セリエーション(序列化)の分析:
- 考古学において、異なる遺跡層から出土する遺物の頻度変化を時系列に沿って可視化し、流行の変遷を確認したい場合。
- 時系列的なカテゴリ比較:
- 複数の項目が時間の経過とともにどのようにシェアや頻度を変化させているかを、グリッド形式で一括比較したい場合。
- アンケート集計結果の可視化:
- 複数の質問項目(行)に対し、回答の選択肢(列)ごとの分布を、棒の太さによって直感的に提示したい場合。
関数 battleship.plot の引数
library(plotrix)
args(battleship.plot)function (x, mar = c(2, 5, 5, 1), col = "white", border = "black",
main = "", xlab = "", ylab = "", xaxlab = NULL, yaxlab = NULL,
cex.labels = 1, maxxspan = 0.45, maxyspan = 0.45)
NULL- x
- 描画対象となる2次元の行列(matrix)またはデータフレームを指定します。
- mar
- グラフの余白(マージン)を
c(bottom, left, top, right)の形式で指定します。ラベルを表示するために、左側と上部の余白を広く確保することが肝要です。
- グラフの余白(マージン)を
- col
- 矩形の塗りつぶし色を指定します。
- border
- 矩形の枠線の色を指定します。
- main, xlab, ylab
- グラフの主タイトル、およびX軸・Y軸のラベルを指定します。
- xaxlab, yaxlab
- 列および行に対して独自のラベルを付与したい場合にベクトル形式で指定します。未指定の場合は行列の名称が流用されます。
- cex.labels
- 軸ラベルの文字サイズを指定します。
- maxxspan
- 矩形が左右に広がる最大半幅を指定します。
- maxyspan
- 矩形の上下方向の最大半幅を指定します。当該の引数により矩形の高さが決定されます。
サンプルコード
以下に、架空のカテゴリデータの頻度分布を可視化するサンプルコードを提示します。
# 1. 解析用サンプルの生成
# 5つのカテゴリ(行)と8つの観測点(列)を持つ行列を作成します
dummy_matrix <- matrix(
c(
2, 5, 8, 12, 10, 6, 3, 1,
10, 15, 12, 8, 4, 2, 1, 0,
0, 1, 3, 7, 15, 20, 12, 8,
5, 5, 5, 5, 5, 5, 5, 5,
1, 2, 4, 8, 16, 8, 4, 2
),
nrow = 5, byrow = TRUE
)
# 行名と列名を設定し、データの識別性を高めます
rownames(dummy_matrix) <- paste("項目", LETTERS[1:5])
colnames(dummy_matrix) <- paste("観測点", 1:8)
# 2. グラフの描画
# battleship.plotを用いて、数値の大きさを矩形の幅で表現します
battleship.plot(
x = dummy_matrix,
main = "カテゴリ別頻度分布の可視化",
xlab = "観測地点の推移",
ylab = "対象項目",
col = "skyblue",
border = "darkblue",
maxxspan = 0.45, # 矩形の最大幅を調整
cex.labels = 0.9
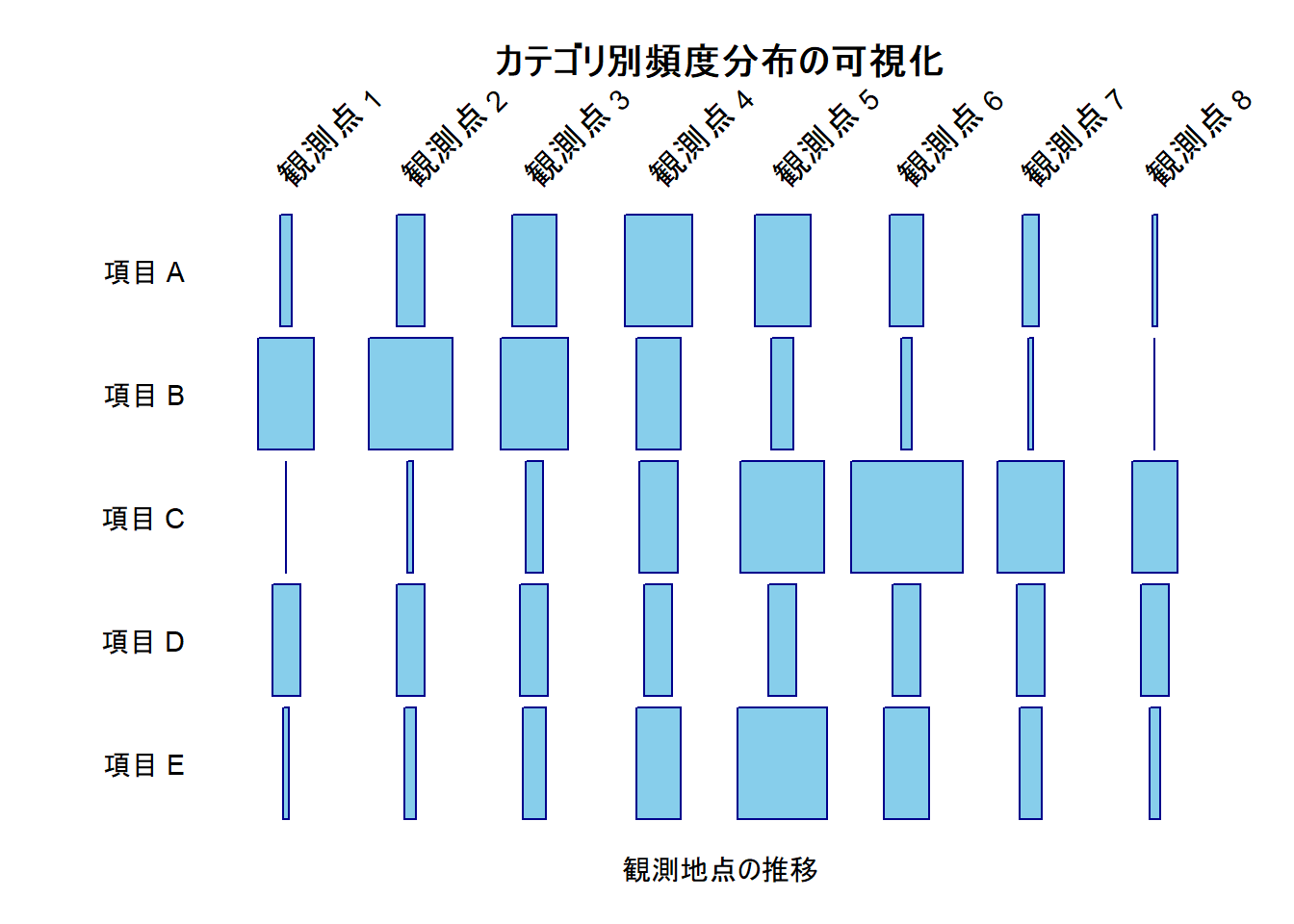
)Figure 1 において、矩形の横幅は行列内の最大値に対する相対的な比率を示しています。
それゆえ、各項目のピークがどの観測点に存在するかを一目で判別することが可能です。
数値が 0 の箇所には矩形が描画されないため(縦線のみ)、出現の有無も明確に提示されます。
以上です。