Rの関数から NLSstAsymptotic {stats} を確認します。
関数 NLSstAsymptotic とは
NLSstAsymptotic は、非線形最小二乗法(Non-Linear Least Squares: NLS)において、「漸近回帰モデル(Asymptotic Regression Model)」のパラメータの初期値(start values)を推定するための関数です。
非線形回帰を行う nls 関数を使用する際、適切な初期値を与えないと収束しない結果を招きます。
本関数は、Self-Starting Modelである SSasymp の内部で使用される補助関数であり、与えられたデータから確からしい初期値を算出します。
この関数が想定しているモデル式は以下の通りです。
\[ y(x) = b_0 + b_1 (1 - e^{-\exp(lrc) \cdot x}) \]
ここで、各パラメータの意味は以下のようになります。
- \(b_0\) (Asymptote origin):
- \(x=0\) の時の \(y\) の値(切片)。
- \(b_1\) (R0 - Asym):
- \(x\) が \(0\) から \(\infty\) まで変化する間の \(y\) の総変化量。
- したがって、最終的な漸近線(Asymptote)の値は \(b_0 + b_1\) となります。
- \(lrc\) (Log Rate Constant):
- 変化率定数の対数値。レート定数を \(k\) とすると、\(k = \exp(lrc)\) です。
関数 NLSstAsymptotic の引数
args(NLSstAsymptotic)function (xy)
NULLgetS3method("NLSstAsymptotic", "sortedXyData")function (xy)
{
xy$rt <- NLSstRtAsymptote(xy)
setNames(coef(nls(y ~ cbind(1, 1 - exp(-exp(lrc) * x)), data = xy,
start = list(lrc = log(-coef(lm(log(abs(y - rt)) ~ x,
data = xy))[[2L]])), algorithm = "plinear"))[c(2,
3, 1)], c("b0", "b1", "lrc"))
}
<bytecode: 0x000002a321494880>
<environment: namespace:stats>getS3method("NLSstRtAsymptote", "sortedXyData")function (xy)
{
in.range <- range(xy$y)
last.dif <- abs(in.range - xy$y[nrow(xy)])
if (match(min(last.dif), last.dif) == 2L)
in.range[2L] + diff(in.range)/8
else in.range[1L] - diff(in.range)/8
}
<bytecode: 0x000002a31f384160>
<environment: namespace:stats>本関数は S3 メソッドであり、特定のクラス sortedXyData に対して動作するように設計されています。
-
xy- 意味: \(x\) と \(y\) のデータを含む
sortedXyDataクラスのオブジェクト。 - 要件: 通常のデータフレームではなく、
stats::sortedXyData関数を使って作成された、xの昇順にソートされた構造体である必要があります。 - コード内での処理:
- まず、補助関数
NLSstRtAsymptote(xy)を呼び出して、データの形状から漸近線(無限遠での値)の概算値rtを推定します。 - 次に、モデルを線形化して
lm(線形回帰)を行い、lrc(レート定数の対数)の初期値を推定します。具体的には \(\log(|y - rt|) \sim x\) の傾きを利用します。 - 最後に、得られた
lrcを固定し、nls関数のalgorithm = "plinear"(部分線形最小二乗法)を使用して、線形パラメータである \(b_0\) と \(b_1\) を推定します。 - 推定された係数ベクトル
c(b0, b1, lrc)を返します。
- まず、補助関数
- 意味: \(x\) と \(y\) のデータを含む
補助関数 NLSstRtAsymptote について
本関数は、漸近線の値をヒューリスティックに推定します。
- データの範囲(range)を確認します。
- 最後のデータ点(xが最大の部分)が、範囲の最大値に近いか最小値に近いかを判定します。
- 最大値に近い場合(増加トレンド): 最大値に範囲の1/8を足した値を漸近線と仮定します。
- 最小値に近い場合(減少トレンド): 最小値から範囲の1/8を引いた値を漸近線と仮定します。
シミュレーションコード
以下に、NLSstAsymptotic の機能を確認するためのサンプルデータを用いたシミュレーションコードを示します。
本シミュレーションでは、以下の手順を行います。
- 真のパラメータを設定し、漸近回帰モデルに従うサンプルデータを生成します。
- データを
sortedXyData形式に変換します。 -
NLSstAsymptoticを使用して、パラメータの初期値を推定します。 - 推定された初期値が、真の値に近いことを確認します。
- その初期値を使って
nlsでモデルを適合させ、結果を可視化します。
なお、有意水準は5%とします。
サンプルデータの作成
# パッケージの読み込み
library(ggplot2)
# 乱数シードの固定
seed <- 20260217
set.seed(seed)
# NLSstAsymptotic 関数による初期値推定のシミュレーション
# 1. サンプルデータの生成
# モデル: y = b0 + b1 * (1 - exp(-exp(lrc) * x))
# 化学反応の進行度や、生物の成長曲線などを模したデータを作成します。
# 真のパラメータ設定
true_b0 <- 10 # x=0 での値(初期値)
true_b1 <- 20 # 総変化量(最終的には 10 + 20 = 30 に収束する)
true_lrc <- log(0.5) # レート定数 k = 0.5, lrc = -0.693
# xデータの作成 (0から10まで)
x_vals <- seq(0, 10, length.out = 30)
# 真のy値の計算
y_true <- true_b0 + true_b1 * (1 - exp(-exp(true_lrc) * x_vals))
# 観測データ (ノイズを付加)
y_obs <- y_true + rnorm(length(x_vals), mean = 0, sd = 1.0)
# データフレーム化
df_sim <- data.frame(x = x_vals, y = y_obs)
# 2. sortedXyData オブジェクトへの変換
# NLSstAsymptotic はこのクラスを引数に取るため、変換が必要です。
xy_data <- sortedXyData(df_sim$x, df_sim$y)
cat("--- データ概要 ---\n")
cat(sprintf("真の b0 (切片): %.2f\n", true_b0))
cat(sprintf("真の b1 (変化幅): %.2f (漸近線 = %.2f)\n", true_b1, true_b0 + true_b1))
cat(sprintf("真の lrc (対数レート): %.4f (k = 0.5)\n\n", true_lrc))
cat("\n--- データの一部を確認 ---\n")
print(str(xy_data))--- データ概要 ---
真の b0 (切片): 10.00
真の b1 (変化幅): 20.00 (漸近線 = 30.00)
真の lrc (対数レート): -0.6931 (k = 0.5)
--- データの一部を確認 ---
Classes 'sortedXyData' and 'data.frame': 30 obs. of 2 variables:
$ x: num 0 0.345 0.69 1.034 1.379 ...
$ y: num 11.3 13.3 16.5 18.4 20.8 ...
NULL NLSstAsymptotic による初期値の推定
# 3. NLSstAsymptotic による初期値の推定
init_vals <- NLSstAsymptotic(xy_data)
cat("--- NLSstAsymptotic による推定初期値 ---\n")
print(init_vals)
cat("\n--- 真の値との比較 ---\n")
cat(sprintf("b0 (推定): %.4f vs (真): %.4f\n", init_vals["b0"], true_b0))
cat(sprintf("b1 (推定): %.4f vs (真): %.4f\n", init_vals["b1"], true_b1))
cat(sprintf("lrc(推定): %.4f vs (真): %.4f\n\n", init_vals["lrc"], true_lrc))--- NLSstAsymptotic による推定初期値 ---
b0 b1 lrc
10.8198641 18.7410742 -0.6720179
--- 真の値との比較 ---
b0 (推定): 10.8199 vs (真): 10.0000
b1 (推定): 18.7411 vs (真): 20.0000
lrc(推定): -0.6720 vs (真): -0.6931\(b_0\) (初期値/切片) の推定
- 結果: 推定値 10.8199 vs 真の値 10.0000
- データには標準偏差 1.0 のノイズが含まれているため、\(x=0\) 付近のデータがたまたま上振れしていれば、推定値もそれに引きずられます。約 0.8 のズレがありますが、データのスケール(0 ~ 30程度)を考えれば許容範囲内であり、
nlsが探索を始める地点として問題ないと考えられます。
\(b_1\) (総変化量) の推定
- 結果: 推定値 18.7411 vs 真の値 20.0000
- 真の値より少し小さく見積もられています。これは \(b_0\) が高めに推定されたことと相関しています(スタートが高すぎたため、そこからの伸びしろを少し小さく見積もってバランスを取ろうとした形です)。それでも、真の値の90%以上を捉えており、モデルのスケール感を適切に認識できています。
\(lrc\) (対数レート定数) の推定
- 結果: 推定値 -0.6720 vs 真の値 -0.6931
- \(lrc\) は曲線の「曲がり具合(収束の速さ)」を決めるパラメータであり、ここが大きく外れると
nlsは収束しません(「勾配が特異」などのエラーになります)。推定値と真の値の差はわずか 0.02 程度であり、適切にカーブの形状を特定できています。
推定された初期値を用いた nls の実行
# 4. 推定された初期値を用いた nls の実行
# NLSstAsymptotic が返した値を start 引数に使ってフィッティングを行います。
fit_nls <- nls(
y ~ b0 + b1 * (1 - exp(-exp(lrc) * x)),
data = df_sim,
start = list(b0 = init_vals["b0"], b1 = init_vals["b1"], lrc = init_vals["lrc"])
)
cat("--- nls による最終的なモデル適合結果 ---\n")
print(summary(fit_nls))--- nls による最終的なモデル適合結果 ---
Formula: y ~ b0 + b1 * (1 - exp(-exp(lrc) * x))
Parameters:
Estimate Std. Error t value Pr(>|t|)
b0.b0 10.81986 0.81135 13.336 2.14e-13 ***
b1.b1 18.74107 0.78959 23.735 < 2e-16 ***
lrc.lrc -0.67202 0.09431 -7.126 1.16e-07 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.092 on 27 degrees of freedom
Number of iterations to convergence: 0
Achieved convergence tolerance: 2.421e-06Number of iterations to convergence: 0
非線形最小二乗法(nls)は、初期値からスタートして、少しずつパラメータを修正しながら最適解を探す工程を繰り返します。
今回の結果は 「0回」 ですので、start 引数で渡された値が、すでに最適解であったことを意味します。
NLSstAsymptotic 内部で実行される plinear(部分線形)アルゴリズムが、今回のサンプルデータに対して有効に機能した結果と言えます。
Parameters
-
b0(切片): 10.82 (真の値 10) -
b1(変化幅): 18.74 (真の値 20) -
lrc(変化率): -0.67 (真の値 -0.69)
すべてのパラメータで Pr(>|t|) が設定した有意水準を下回っていることが確認できます。ノイズ(標準偏差1.0)の影響で真の値から多少のズレはありますが、95%信頼区間などを考慮すれば、真の値を十分にカバーする妥当な推定結果です。
Residual standard error: 1.092
この値は、モデルが説明しきれなかった誤差(残差)の標準偏差を表します。
シミュレーションデータの生成時に設定したノイズの標準偏差は sd = 1.0 でした。
推定された 1.092 は設定値に近く、モデルがデータの構造(シグナル)を過不足なく吸い上げ、純粋なノイズ部分だけを残差として残したことを示唆しています。過学習も過小適合もしていない状態です。
結果の可視化
# 5. 結果の可視化
# 予測値の取得
df_sim$fitted <- predict(fit_nls)
# NLSstAsymptotic が推定した初期値の曲線も計算(初期推定の精度確認用)
df_sim$init_fit <- init_vals["b0"] + init_vals["b1"] * (1 - exp(-exp(init_vals["lrc"]) * df_sim$x))
p1 <- ggplot(df_sim, aes(x = x, y = y)) +
# 観測データ
geom_point(aes(color = "観測データ"), size = 2, alpha = 0.7) +
# 真の曲線
geom_line(aes(y = y_true, color = "真の曲線"), linewidth = 1, linetype = "dashed") +
# NLSstAsymptoticによる初期推定
geom_line(aes(y = init_fit, color = "NLSstAsymptotic (初期値)"), linewidth = 2.5, linetype = "dotted") +
# 最終的なnls適合
geom_line(aes(y = fitted, color = "nls適合後"), linewidth = 1) +
labs(
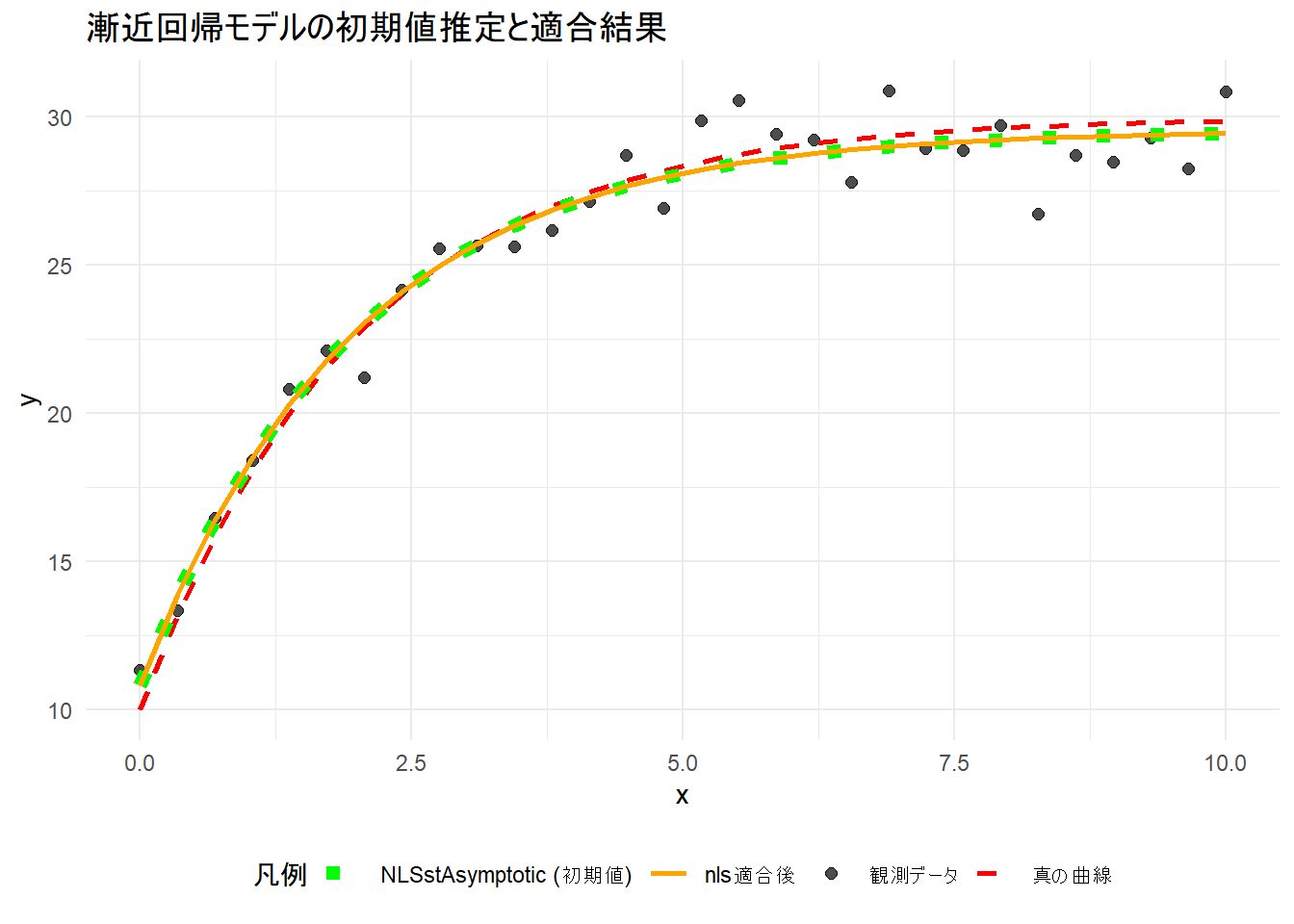
title = "漸近回帰モデルの初期値推定と適合結果",
x = "x", y = "y",
color = "凡例"
) +
scale_color_manual(values = c(
"観測データ" = "black",
"真の曲線" = "red",
"NLSstAsymptotic (初期値)" = "green",
"nls適合後" = "orange"
)) +
theme_minimal() +
theme(legend.position = "bottom")
print(p1)観測データ(黒い点)
黒い点は、真のモデルにノイズ(誤差)を加えた「観測データ」です。
\(x\) が増えるにつれて \(y\) が急激に上昇し、次第に傾きが緩やかになって一定の値(漸近線)に近づいていく様子が見て取れます。
真の曲線(赤の破線)
ノイズのない真のモデル(\(y = 10 + 20(1 - e^{-0.5x})\))です。
黒い点群が、この赤い破線を中心にばらついていることが確認できます。
NLSstAsymptoticによる初期値(緑の点線)
緑の点線は、赤の破線(正解)に近い位置を、初期値の段階で、通っています。
nls適合後(オレンジの実線)
緑の初期値を出発点として、nls 関数が微調整を行った最終的な回帰直線です。
緑の点線と重なっており 「反復回数が0回」であった結果を視覚的に確認できます
以上です。