Rによる時系列過程の判定

Rによる 時系列過程 の判定を試みます。

なお、本ポストでは 情報量規準（AIC,BICなど） は利用せずに、自己相関関数(ACF) および 偏自己相関関数(PACF) のみを利用します。

始めに MA(2)過程、AR(1)過程 および ARMA(1,1)過程 のサンプルデータを作成します。

seed <- 20250422
set.seed(seed)

# サンプルサイズ
n_sample <- 200

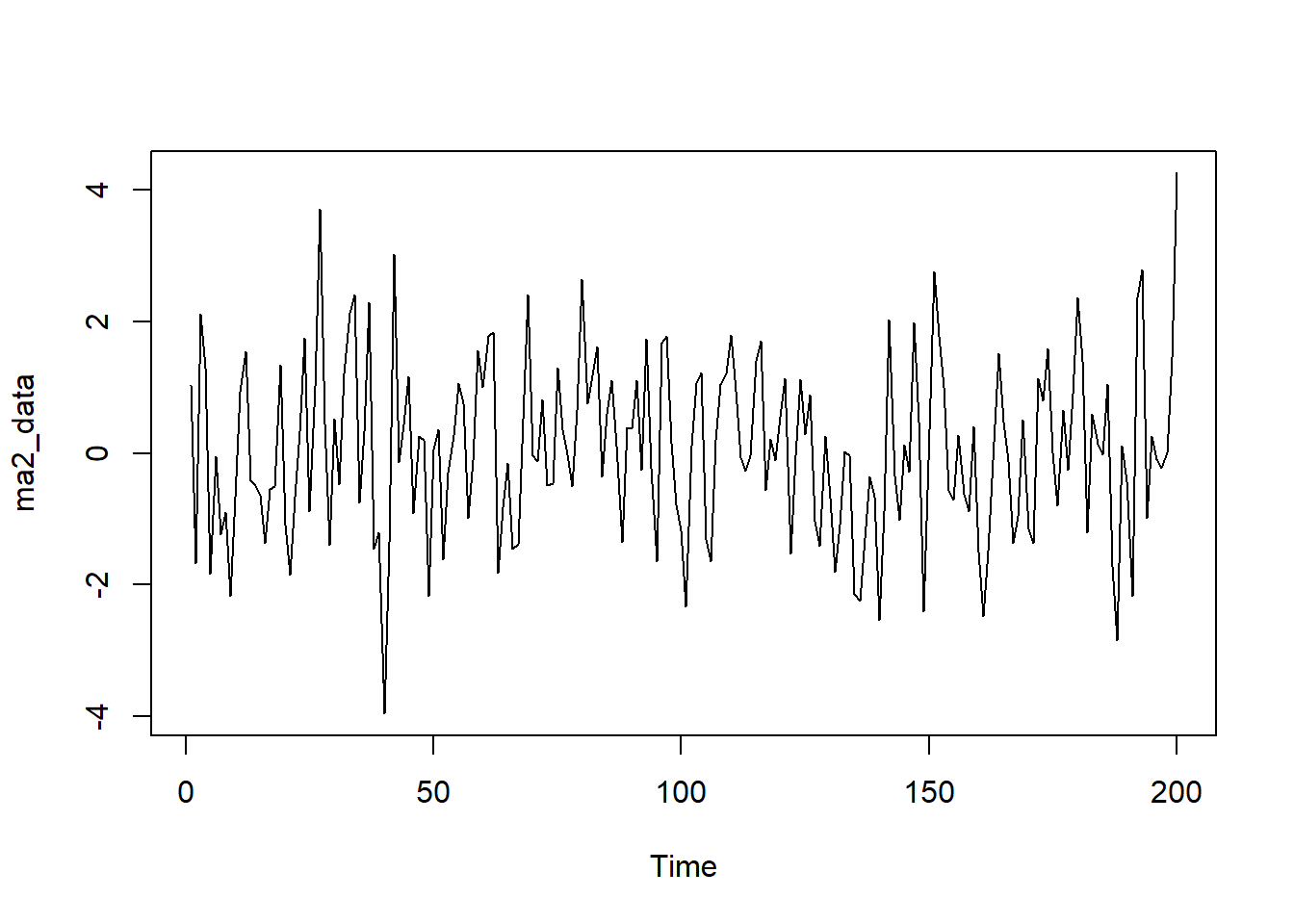
# 1 MA(2)過程のデータ生成
# モデル: Y_t = ε_t + 0.7 * ε_{t-1} - 0.5 * ε_{t-2}
# 過程: ラグ2までの誤差項の影響を受ける
ma2_data <- arima.sim(model = list(ma = c(0.7, -0.5)), n = n_sample)

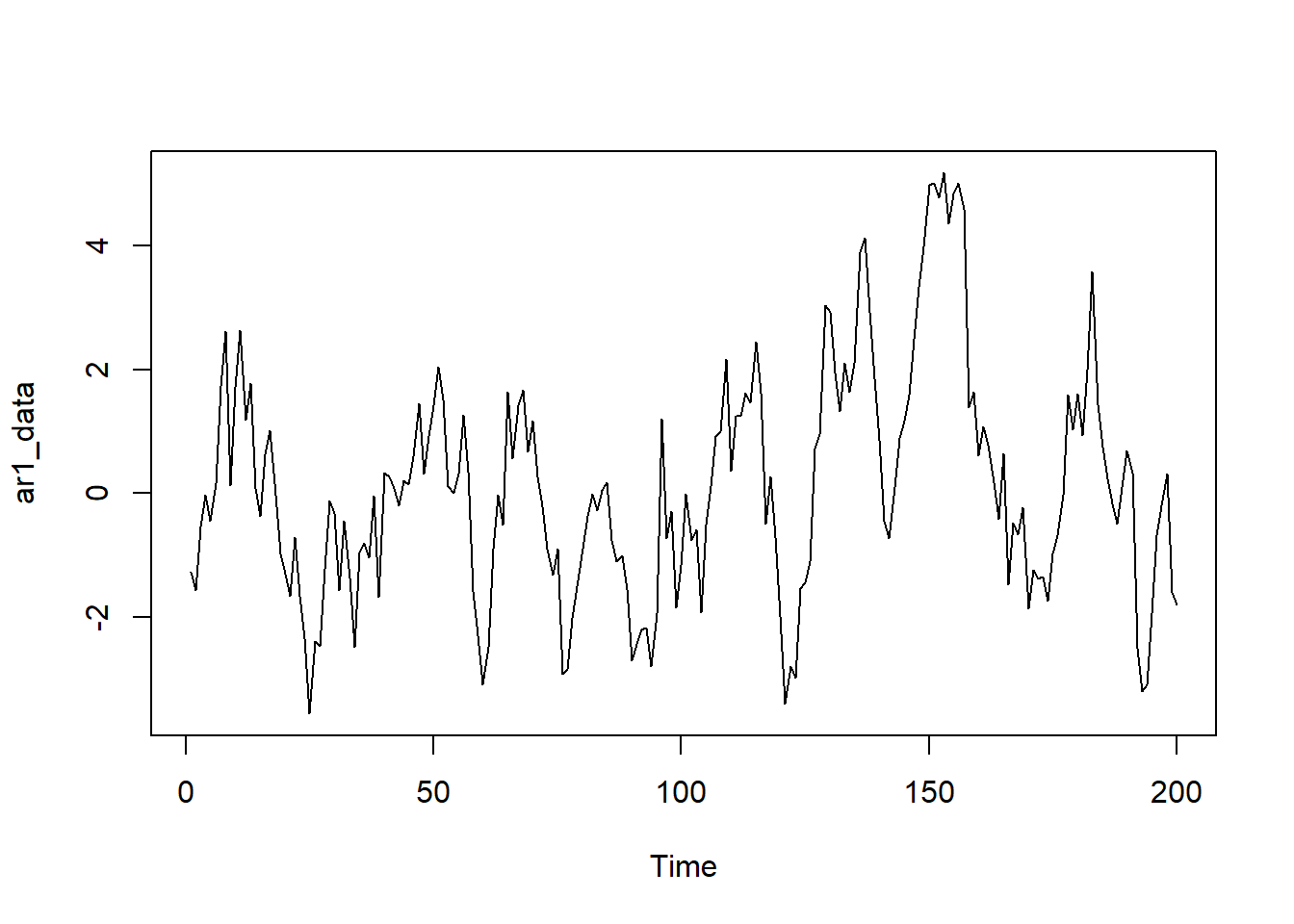
# 2 AR(1)過程のデータ生成
# モデル: Y_t = 0.9 * Y_{t-1} + ε_t
# 過程: 1期前の自身の値の影響を受ける
ar1_data <- arima.sim(model = list(ar = 0.9), n = n_sample)

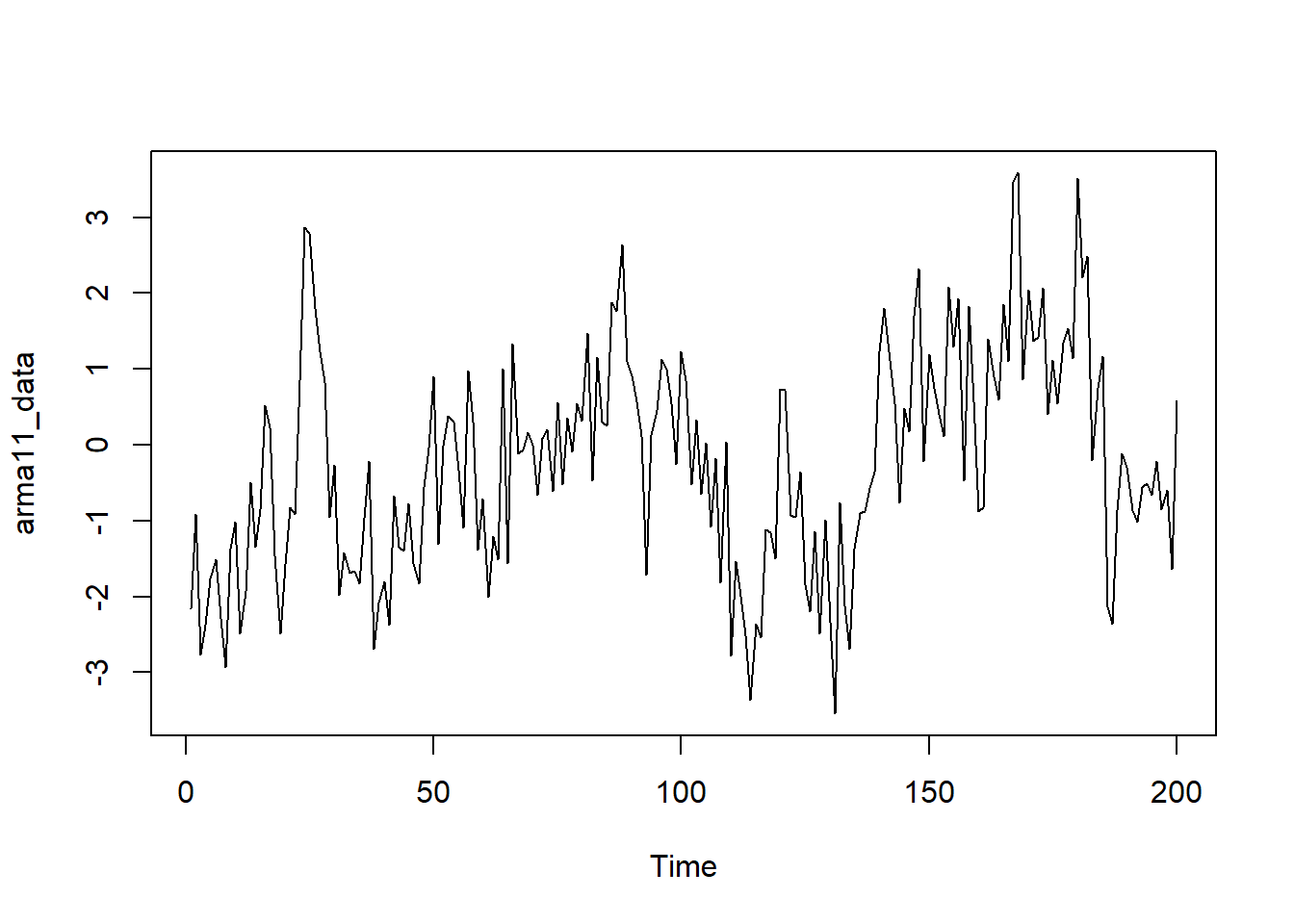
# 3 ARMA(1, 1)過程のデータ生成
# モデル: Y_t = 0.9 * Y_{t-1} + ε_t - 0.5 * ε_{t-1}
# 過程: 1期前の自身の値と1期前の誤差項の影響を受ける
arma11_data <- arima.sim(model = list(ar = 0.9, ma = -0.5), n = n_sample)
(a) MA(2)
(b) AR(1)
(c) ARMA(1,1)
Figure 1: 3つの時系列過程

続いてそれぞれの過程の自己相関関数を確認します。

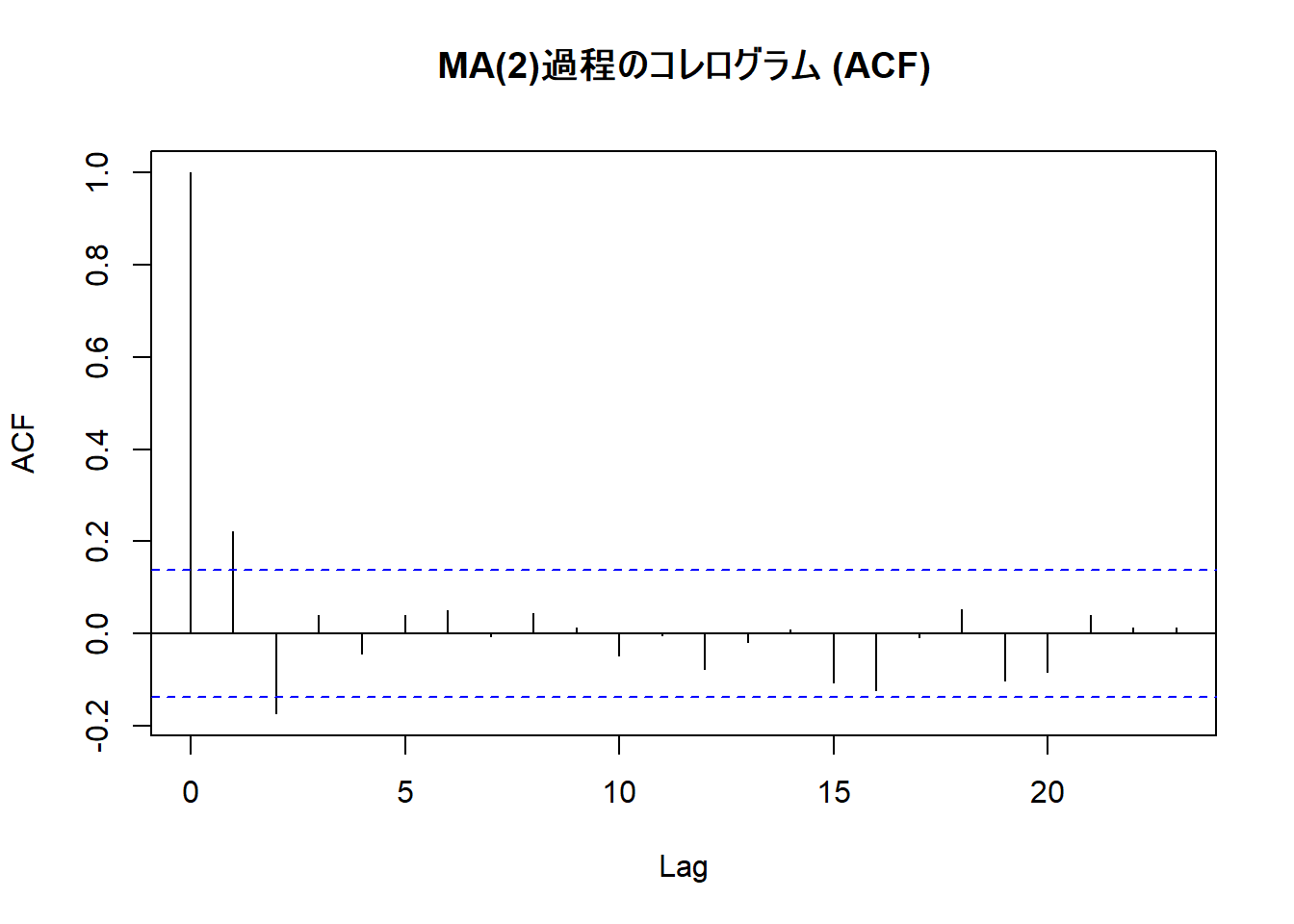
始めに MA(2)過程 を確認します。

acf(ma2_data, main = "MA(2)過程のコレログラム (ACF)",ci = 0.95)
Figure 2: MA(2)過程のコレログラム(ACF)
  1. MAモデルは、過去の有限個の誤差項（ホワイトノイズ）の線形和で現在の値が決まるモデルです。MA(q)モデルは次数qまでの誤差項の影響を受けます。
  2. ラグ1とラグ2の自己相関のみが、有意水準5%ラインを超えています。
  3. ラグ3以降の自己相関は、急激に小さくなり、有意水準5%ラインを超えていません。
  4. 自己相関が特定のラグ（この場合はラグ2）で「打ち切られる」パターンは、MA過程の特徴です。
  5. よって、ACFからは MA(2)過程が示唆されます。

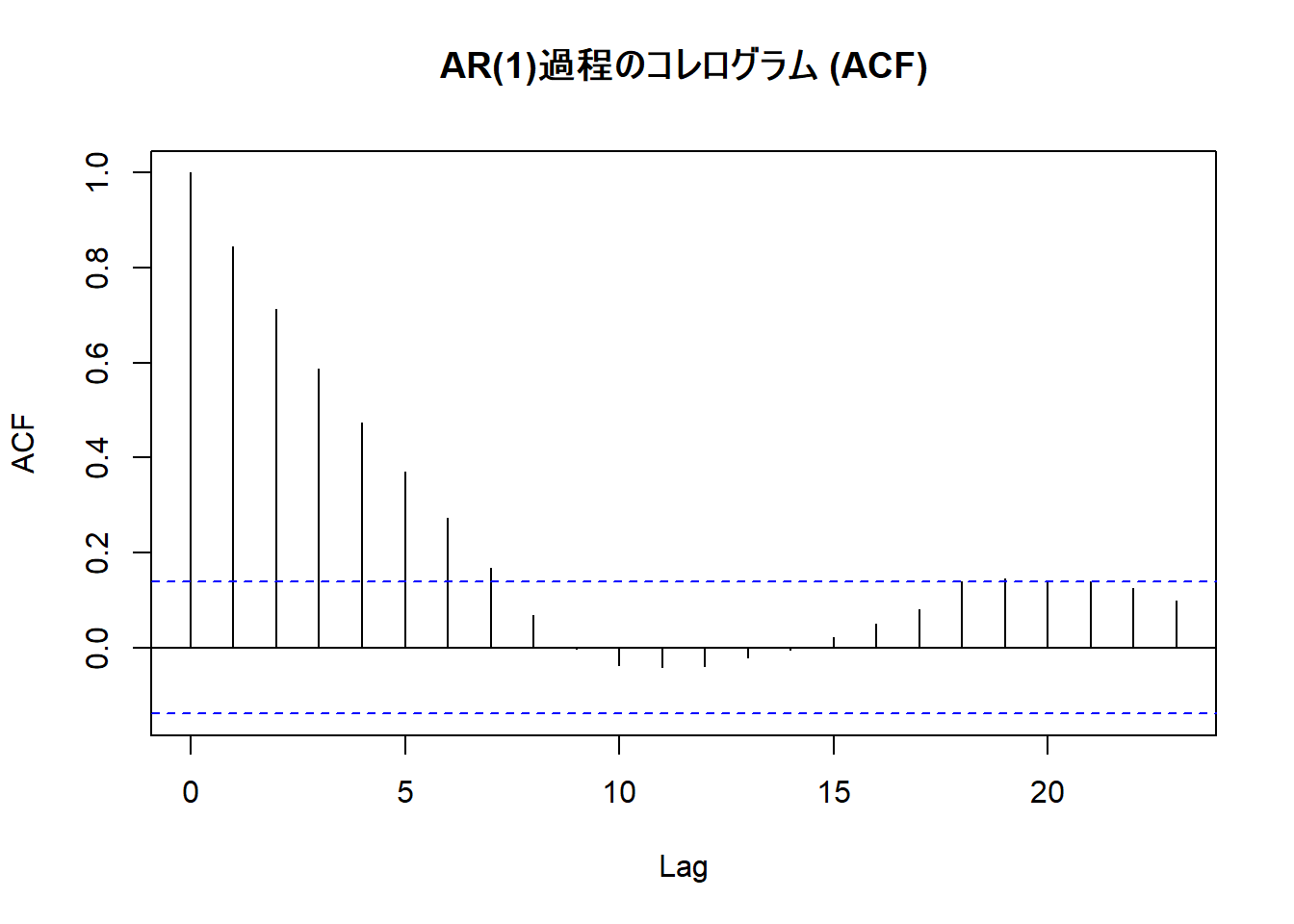
続いて AR(1)過程 です。

acf(ar1_data, main = "AR(1)過程のコレログラム (ACF)",ci = 0.95)
Figure 3: AR(1)過程のコレログラム(ACF)
  1. ARモデルは、過去の有限個の自分自身の値の線形和で現在の値が決まるモデルです。AR(p)モデルはp期前までの自身の値の影響を受けます。
  2. ラグ1の自己相関が最も高く、ラグが増えるにつれて自己相関の値が徐々に小さくなっています。
  3. MA過程のように(Figure 2)、あるラグで急激に0になる（有意水準ラインを超えない）様子は見られません。
  4. このように、自己相関がラグの増加とともに徐々に減衰していく（指数関数的に減衰する）パターンは、AR過程またはARMA過程の特徴です。
  5. このACFだけを見ると、AR過程かARMA過程が示唆されます。
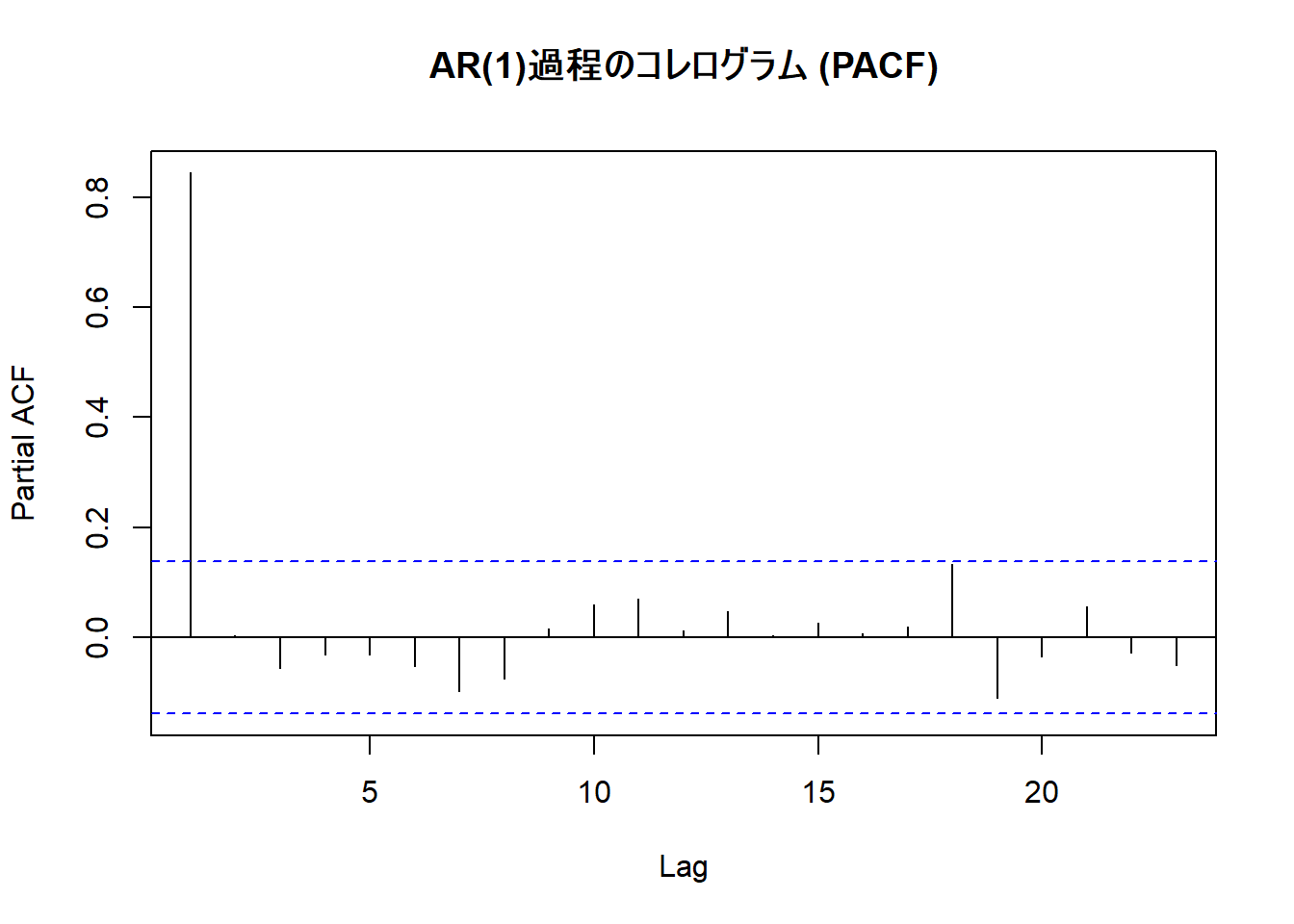
  6. AR過程の次数を特定する方法の一つはPACF（偏自己相関関数）による確認です。AR(p)過程のPACFはラグp+1以降で急激に0になります。
Rで偏自己相関関数
Rで 偏自己相関関数(Partial autocorrelation function) を試みます。始めに AR(1) のサンプルデータを作成します。seed <- 20250418set.seed(seed)n <- 200 # サンプ...
www.saecanet.com
2025.04.18
pacf(ar1_data, main = "AR(1)過程のコレログラム (PACF)",ci = 0.95)
Figure 4: AR(1)過程のコレログラム(PACF)

ラグ1以降は全て有意水準ラインを超えていません。

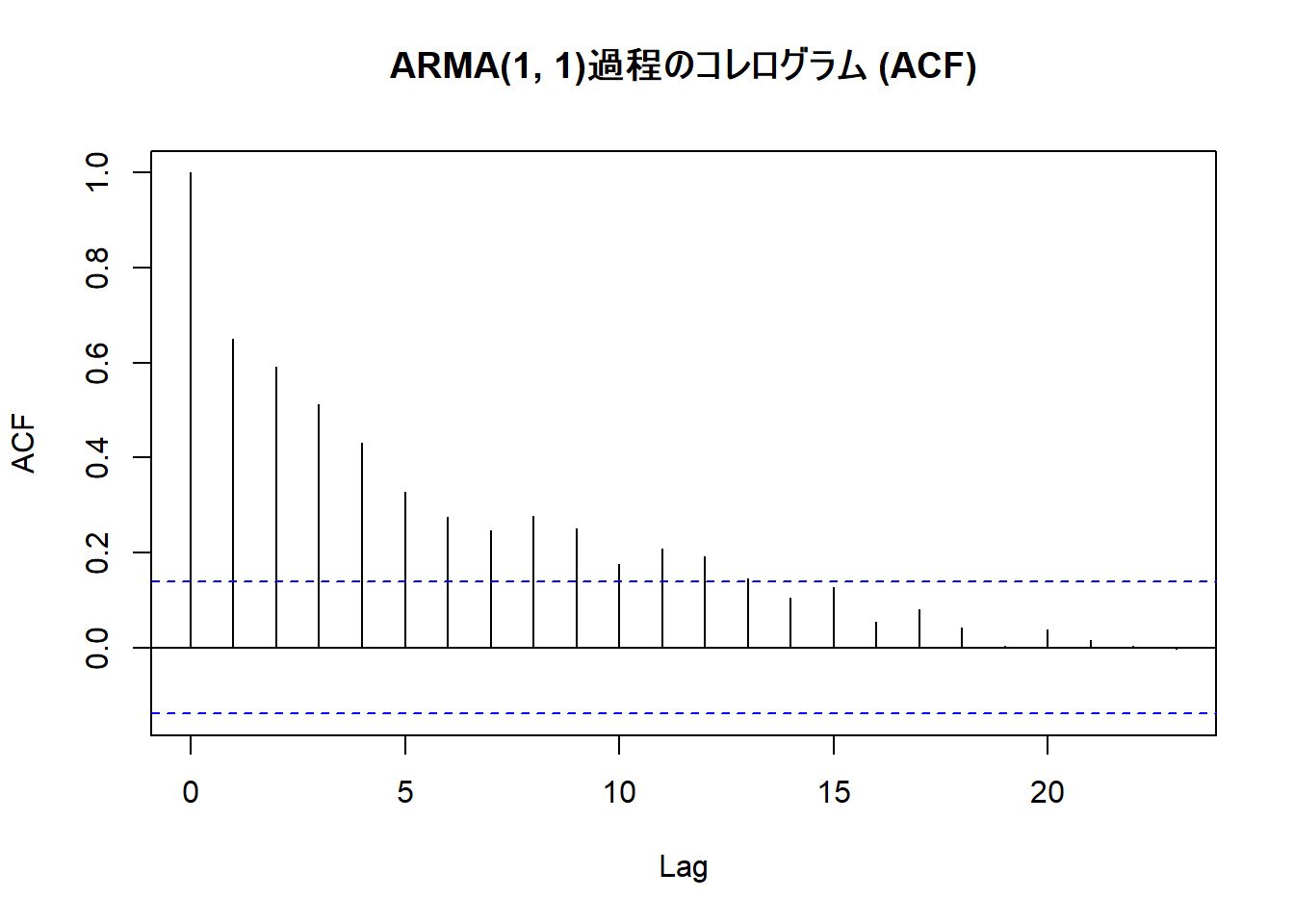
最後は ARMA(1,1)過程 です。

acf(arma11_data, main = "ARMA(1, 1)過程のコレログラム (ACF)",ci = 0.95)
Figure 5: ARMA(1,1)過程のコレログラム(ACF)
  1. ARMAモデルは、AR過程とMA過程の両方の性質を併せ持つモデルです。ARMA(p,q)モデルは、p期前までの自身の値と、q期前までの誤差項の影響を受けます。
  2. MA過程のような急激な打ち切り(Figure 2)は見られないのと同時に、AR(1)過程と同様に自己相関が徐々に減衰していくパターンが見られます(Figure 3)。
  3. ラグ2以降の減衰の仕方はAR(1)の例とは、ARMAのMA部分が影響し、異なっています。
  4. このACFだけを見ると、AR過程かARMA過程が示唆されます。
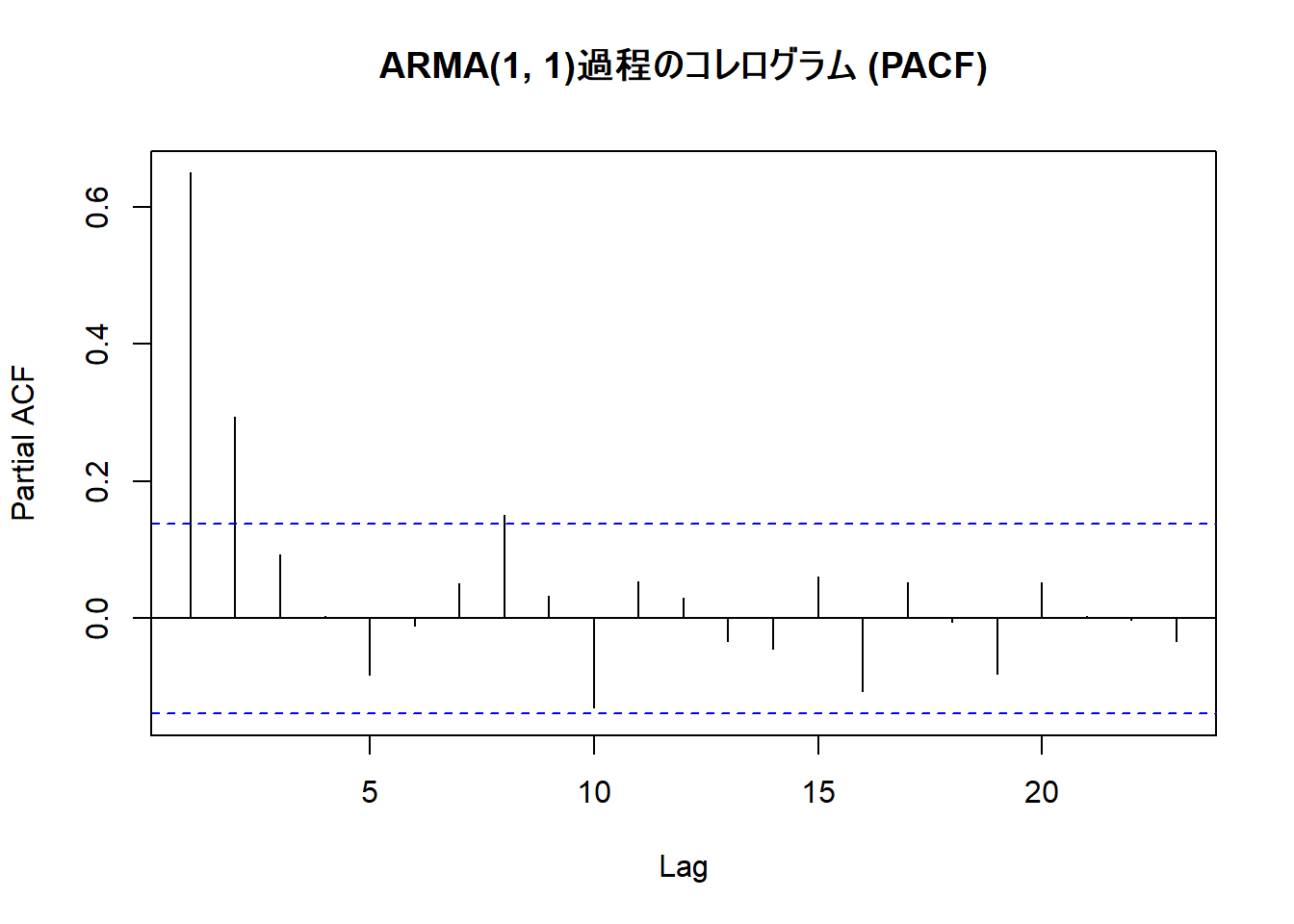
  5. PACFを確認します。
pacf(arma11_data, main = "ARMA(1, 1)過程のコレログラム (PACF)",ci = 0.95)
Figure 6: ARMA(1,1)過程のコレログラム(PACF)

AR(1)過程のPACF(Figure 4)と異なり、ラグ2も有意水準ラインを超えています。

以上です。