Rで ランダム化比較試験:クロスオーバー試験(Crossover study) のシミュレーションを試みます。
なお、以下の架空のストーリー中の会社名、商品名は実在の団体や商品とは関係ありません。
【背景】
医療機器メーカーの「痛みよさらば社」は、慢性的な緊張型頭痛を持つ人々の痛みを和らげるための、新しい携帯型低周波治療器「イタミヲトール」を開発しました。この治療器は、こめかみに装着して微弱な電気刺激を与えることで、痛みを緩和する仕組みです。
【研究の目的】
この研究の目的は、慢性的な緊張型頭痛を持つ成人において、新治療器「イタミヲトール」が、見た目は同じだが電気刺激の出ない「シャムデバイス(偽の治療器)」と比較して、主観的な痛みのスコアを軽減させる効果があるかを科学的に検証することです。
【研究デザイン:クロスオーバー試験】
治療器の効果は使用中の一時的なものと考えられ、使用をやめれば効果はなくなる(キャリーオーバー効果が少ない)と想定されます。
- 参加者: 慢性的(週に2回以上)な緊張型頭痛に悩む成人40名。
- 介入内容:
- 介入A (Treatment): 「イタミヲトール」を頭痛時に30分間使用する。
- 介入B (Sham): 見た目が全く同じ「シャムデバイス」を頭痛時に30分間使用する。
- ランダム化と試験の流れ:
- 参加者40名は、ランダムに2つのシーケンス(順序)グループに分けられます。
- グループ1 (20名): 最初の4週間は介入A (本物) を使用し、次の4週間は介入B (偽物) を使用する。(A→Bシーケンス)
- グループ2 (20名): 最初の4週間は介入B (偽物) を使用し、次の4週間は介入A (本物) を使用する。(B→Aシーケンス)
- 最初の4週間(第1期)が終了した後、2週間のウォッシュアウト期間(Washout Period)を設けます。これは、第1期の治療効果が第2期に持ち越される(キャリーオーバー効果)のを防ぐためです。この期間は、どちらのデバイスも使用しません。
- ウォッシュアウト期間の後、グループ1は介入Bに、グループ2は介入Aに切り替えて、さらに4週間(第2期)試験を続けます。
- 参加者40名は、ランダムに2つのシーケンス(順序)グループに分けられます。
- 盲検化: 二重盲検で行います。参加者も評価者も、各期間でどちらのデバイス(本物か偽物か)を使用しているかを知りません。
- 評価項目:
- 主要評価項目: 各期間の最終週における「平均疼痛スコア」。痛みがない状態を0、想像しうる最悪の痛みを10とする11段階のスケール(NRS: Numerical Rating Scale)で自己評価してもらいます。
- 仮説: 同じ参加者において、「イタミヲトール」を使用した期間の平均疼痛スコアは、「シャムデバイス」を使用した期間のスコアよりも低くなるだろう。
- 統計検定における有意水準: 5%とします。
【ストーリーの流れ】
- 参加者40名は、A→Bシーケンスか、B→Aシーケンスかにランダムに割り振られます。
- 第1期(4週間)、割り振られたデバイスを使用し、痛みを記録します。
- 2週間のウォッシュアウト期間に入ります。
- 第2期(4週間)、前回とは逆のデバイスを使用し、再び痛みを記録します。
- 試験終了後、データが収集され、開鍵が行われます。
- データ解析チームが、各個人の中での「本物のデバイス使用時」と「偽物のデバイス使用時」の疼痛スコアを比較し、統計的な差を評価します。
続いてシミュレーションに入ります。
ステップ1: 初期設定
# パラメータ設定
N_total <- 40 # 全参加者数
N_group <- N_total / 2 # 各シーケンスグループの参加者数ステップ2: データフレームの作成とランダム化
参加者データを作成し、ランダムにシーケンス(A_then_B または B_then_A)を割り当てます。
seed <- 20250614
set.seed(seed)
# 参加者データフレームの作成
crossover_data <- data.frame(
participant_id = 1:N_total
)
# ランダムにシーケンスを割り当てる
crossover_data$sequence <- sample(
rep(c("A_then_B", "B_then_A"), times = N_group)
)
head(crossover_data) participant_id sequence
1 1 A_then_B
2 2 A_then_B
3 3 A_then_B
4 4 A_then_B
5 5 A_then_B
6 6 B_then_Aステップ3: 結果(疼痛スコア)の生成
クロスオーバー試験の構造に合わせて、各期(Period 1, Period 2)の疼痛スコアを生成します。
- 基礎疼痛スコア: 個人差を表現します。平均7点、標準偏差1の個人ごとのベースラインの痛みを持つと仮定します。
- シャムデバイスの効果: 偽のデバイスでも、期待感から痛みが平均0.5点軽減するとします(プラセボ効果)。
- イタミヲトールの効果: 本物のデバイスは、シャム効果に加えて、さらに1.5点痛みを軽減するとします(合計-2.0点)。
library(dplyr)
set.seed(seed)
# 個人の基礎となる疼痛スコアを生成(個人差を表現)
crossover_data$base_pain <- rnorm(N_total, mean = 7, sd = 1)
# 各期間の疼痛スコアを生成
# case_whenでシーケンスと期間に応じて計算式を変える
crossover_data <- crossover_data %>%
mutate(
# 第1期のスコア
score_period1 = case_when(
sequence == "A_then_B" ~ base_pain - 2.0 + rnorm(n(), 0, 0.5), # 介入A (本物)
sequence == "B_then_A" ~ base_pain - 0.5 + rnorm(n(), 0, 0.5) # 介入B (偽物)
),
# 第2期のスコア
score_period2 = case_when(
sequence == "A_then_B" ~ base_pain - 0.5 + rnorm(n(), 0, 0.5), # 介入B (偽物)
sequence == "B_then_A" ~ base_pain - 2.0 + rnorm(n(), 0, 0.5) # 介入A (本物)
)
)
head(crossover_data) participant_id sequence base_pain score_period1 score_period2
1 1 A_then_B 6.484618 5.578454 5.646023
2 2 A_then_B 7.055205 4.594610 6.606249
3 3 A_then_B 6.820065 4.943852 6.200570
4 4 A_then_B 9.374069 7.517271 8.751362
5 5 A_then_B 6.629103 3.730362 5.571945
6 6 B_then_A 6.729727 6.160991 4.873012ステップ4: データ形式の変換と可視化
各行が「1人の参加者の1期間のデータ」を表すようにデータを変換します。
# 横長から縦長データに変換
long_data <- crossover_data %>%
# 期間ごとのスコアを1つの列にまとめる
tidyr::pivot_longer(
cols = c(score_period1, score_period2),
names_to = "period",
values_to = "pain_score"
) %>%
# 各期間でどちらの介入を受けたかを明確にする
mutate(
intervention = case_when(
(sequence == "A_then_B" & period == "score_period1") ~ "Treatment",
(sequence == "A_then_B" & period == "score_period2") ~ "Sham",
(sequence == "B_then_A" & period == "score_period1") ~ "Sham",
(sequence == "B_then_A" & period == "score_period2") ~ "Treatment"
)
)
head(long_data, 10)# A tibble: 10 × 6
participant_id sequence base_pain period pain_score intervention
<int> <chr> <dbl> <chr> <dbl> <chr>
1 1 A_then_B 6.48 score_period1 5.58 Treatment
2 1 A_then_B 6.48 score_period2 5.65 Sham
3 2 A_then_B 7.06 score_period1 4.59 Treatment
4 2 A_then_B 7.06 score_period2 6.61 Sham
5 3 A_then_B 6.82 score_period1 4.94 Treatment
6 3 A_then_B 6.82 score_period2 6.20 Sham
7 4 A_then_B 9.37 score_period1 7.52 Treatment
8 4 A_then_B 9.37 score_period2 8.75 Sham
9 5 A_then_B 6.63 score_period1 3.73 Treatment
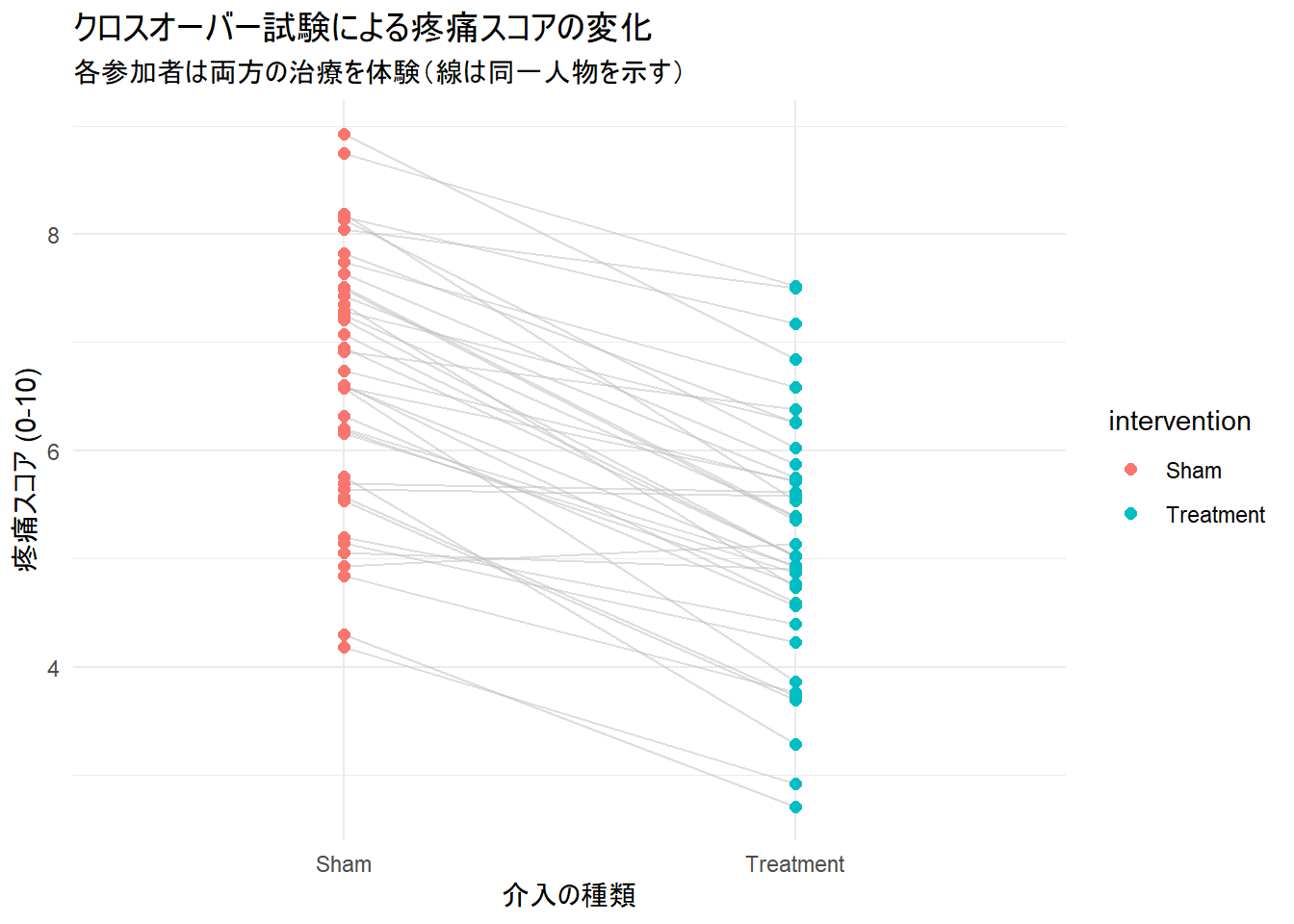
10 5 A_then_B 6.63 score_period2 5.57 Sham 次に、結果を可視化します。各参加者が両方の介入を体験しているので、個人内の変化が分かるように線で結んでプロットします。
library(ggplot2)
ggplot(long_data, aes(x = intervention, y = pain_score, group = participant_id)) +
geom_line(color = "gray", alpha = 0.5) + # 各個人の変化を線で結ぶ
geom_point(aes(color = intervention), size = 2) + # 各点のプロット
labs(
title = "クロスオーバー試験による疼痛スコアの変化",
subtitle = "各参加者は両方の治療を体験(線は同一人物を示す)",
x = "介入の種類",
y = "疼痛スコア (0-10)"
) +
theme_minimal()グラフを見ると、多くの参加者(灰色の線)が、Sham(偽物)からTreatment(本物)に変わるとスコアが下がっている(痛みが改善している)傾向が見て取れます。
ステップ5: 統計的検定(対応のあるt検定)
クロスオーバー試験では、同じ個人の中での2つの条件(TreatmentとSham)の差を比較しますので、対応のあるt検定 (Paired t-test) を用います。
なお、引数は以下の通りとします。
-
alternative = "two.sided"(両側検定)- 意味: 「2つの条件(TreatmentとSham)で測定された値の平均に差があるかどうか」を検定します。つまり、「治療器の効果がプラス(痛みが軽減)であっても、マイナス(痛みが悪化)であっても」、とにかく差があるか否かを検定します。
- 選択の理由:
- 科学的な客観性の担保: 研究を始める時点では、「治療器が痛みを和らげる」という仮説を持っています。しかし、科学的な検証としては、予期せぬ有害事象(例えば、電極の刺激が不快で逆に痛みを増強させるなど)の可能性も完全に排除すべきではないため、両側検定を選択します。
- 結論の信頼性: もし片側検定(例:
alternative = "less"、つまりTreatment群のスコアがSham群より「小さい」ことだけを検定)を使って有意な結果が出た場合、「最初から良い結果が出ることだけを期待していたのでは?」という批判を受ける可能性があります。
-
mu = 0- 意味: 帰無仮説(棄却したい仮説)として、「2つの条件における測定値の差の平均が0である」と設定します。クロスオーバー試験の文脈で言えば、「各個人における (Sham使用時のスコア – Treatment使用時のスコア) の平均値が0である」ということです。
- 選択の理由:
- 検証したいことの本質: 知りたいのは、「イタミヲトールに効果があるかないか」です。その最も基本的な問いは、「もし効果が全くないとしたら、本物の治療器と偽物の治療器で結果に差は出ないはずだ」という考え方、つまり
mu = 0に基づきます。なお、参考として例えば、もし過去の研究で「偽薬でも平均0.2点くらいは痛みが改善する」というデータがあり、「新薬はそれ以上の効果があるか?」を直接検証したいのであれば、mu = 0.2のような設定も考えられます。
- 検証したいことの本質: 知りたいのは、「イタミヲトールに効果があるかないか」です。その最も基本的な問いは、「もし効果が全くないとしたら、本物の治療器と偽物の治療器で結果に差は出ないはずだ」という考え方、つまり
-
paired = TRUE-
paired = TRUEの意味:独立した2つのグループを比較するのではなく、ペアになったデータ間の「差」を計算し、その「差のデータ(1つの標本)」に対して1標本のt検定を行うのと同じことになります。- 具体的には、各参加者について
d = pain_score_sham - pain_score_treatmentという差を計算します。 - そして、この
dという新しいデータセットの平均が、mu=0と有意に異なるかどうかを検定します。 - このように、対応のあるt検定は内部的に「差のデータ」という1つのグループに対する検定に変換されます。比較対象となるグループが1つしかないため、グループ間の分散の等質性(
var.equal)を問う必要がなくなります。 - したがって、
paired = TRUEを指定した場合、var.equal引数は無視されます。
- 具体的には、各参加者について
- 選択の理由:
- 研究デザインとの一致: クロスオーバー試験は、各参加者が自分自身の対照(コントロール)となる「個人内比較」のデザインです。これにより、個人差(もともとの痛みの感じやすさ、生活習慣など)が結果に与える影響を排除できます。
-
# 対応のあるt検定の実施
# 両方のベクトルの順序を participant_id 順に揃えるために
# データを participant_id でソートしてからベクトルを抽出
treatment_scores_sorted <- long_data %>%
filter(intervention == "Treatment") %>%
arrange(participant_id) %>% # participant_idで昇順に並べ替え
pull(pain_score)
sham_scores_sorted <- long_data %>%
filter(intervention == "Sham") %>%
arrange(participant_id) %>% # participant_idで昇順に並べ替え
pull(pain_score)
# 対応のあるt検定を実行
t_test_result_paired <- t.test(treatment_scores_sorted, sham_scores_sorted, paired = TRUE)
# 結果の表示
print(t_test_result_paired)
Paired t-test
data: treatment_scores_sorted and sham_scores_sorted
t = -12.416, df = 39, p-value = 3.984e-15
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
-1.688584 -1.215485
sample estimates:
mean difference
-1.452034 ステップ6: 結果の解釈と結論
- mean difference: 差の平均は
-1.452034でした。これは、本物の治療器を使った方が、偽物を使った時よりも平均で約1.452034 点、疼痛スコアが低いことを示しています。 - 結論: p値(3.984e-15)が研究デザインで定めた有意水準を下回っていますので、「2つの介入に差はない」という帰無仮説は棄却され、観測された疼痛スコアの差は統計的に有意であると判断します。
【シミュレーション全体のまとめ】
このシミュレーションは、「痛みよさらば社」が行ったクロスオーバー試験を模したものです
この結果に基づき、同社は「新しい治療器『イタミヲトール』は、慢性的な緊張型頭痛の痛みを軽減する上で、偽のデバイスよりも統計的に有意に優れた効果がある」と判断することができます。
以上です。