Rの関数:wilcox.test {stats}:ウィルコクソンの符号順位検定(1標本の場合)

関数 wilcox.test とは

wilcox.test は、ノンパラメトリック仮説検定関数であり、平均や分散などの分布形状を仮定せずに「位置（location）」の違いを検定するために用いられます。

この関数は 実質的に 2 種類の検定を実装しており、入力の与え方によって自動的に切り替わります。

wilcox.test が実装している 2 つの検定

1. Wilcoxon Signed Rank Test
   • 入力形式 : wilcox.test(x, mu = ...)
   • 適用 : 1標本 / 対応あり
2. Wilcoxon Rank Sum Test
   • 入力形式 : wilcox.test(x, y)
   • 適用 : 2標本・独立

wilcox.test のコードでは、y が NULL か否かで 別のロジックが走ります。

関数 wilcox.test の引数

args(getS3method("wilcox.test", class = "default"))

function (x, y = NULL, alternative = c("two.sided", "less", "greater"), 
    mu = 0, paired = FALSE, exact = NULL, correct = TRUE, conf.int = FALSE, 
    conf.level = 0.95, tol.root = 1e-04, digits.rank = Inf, ...) 
NULL

1. x
   • 第1のデータベクトル（数値型）。
   • 数値ベクトルである必要があります。欠損値 (NA) は除外されます。
2. y
   • 第2のデータベクトル（数値型）。省略可能。
   • NULL の場合（デフォルト）：x に対する1標本検定が行われます。
   • 指定された場合：x と y の2標本検定が行われます。paired = TRUE の場合は x と y の長さが等しい必要があります。
3. alternative
   • 対立仮説の種類を指定します。
   • 選択肢:
     • "two.sided" (デフォルト): 両側検定（分布の位置が異なる）。
     • "greater": 片側検定（x の方が位置が右側にある／確率的に大きい）。
     • "less": 片側検定（x の方が位置が左側にある／確率的に小さい）。
4. mu
   • 帰無仮説における位置母数の差（または1標本の場合の位置そのもの）。
   • デフォルト: 0。つまり、2標本の場合は「位置のズレ（location shift）が0である」、1標本の場合は「分布の中心位置が0である」ことが帰無仮説となります。
5. paired
   • 対応のある検定を行うかどうかの論理値。
   • デフォルト: FALSE（独立した2標本の検定＝順位和検定）。
   • TRUE に設定すると、対応のある検定（符号付き順位検定）を実行します。この際、x と y はペアごとの差分として処理されます。
6. exact
   • 正確なP値（Exact p-value）を計算するかどうかの論理値。
   • デフォルト: NULL。
   • NULL の場合、サンプルサイズが50未満で、かつタイ（同順位）が存在しない場合に TRUE となり、正確なP値が計算されます。
   • サンプルサイズが大きい、またはタイがある場合は、正規近似を用いたP値が計算されます。
7. correct
   • 正規近似を行う際に、連続性の補正（Continuity Correction）を適用するかどうかの論理値。
   • デフォルト: TRUE。
   • 離散的な順位統計量を連続的な正規分布で近似する際の誤差を減らすための補正です。
8. conf.int
   • 位置母数の差（または1標本の場合は位置）の信頼区間を計算するかどうかの論理値。
   • デフォルト: FALSE。
   • ここで計算される推定値は、ホッジス・レーマン推定量（Hodges-Lehmann estimator）です。
   • 推定量の意味
     • Signed Rank : 差の疑似中央値
     • Rank Sum : (X - Y) の中央値
9. conf.level
   • 信頼区間の信頼水準。
   • デフォルト: 0.95（95%信頼区間）
10. tol.root
    • 信頼区間などを計算する際の数値探索における許容誤差。
    • デフォルト: 1e-04
11. digits.rank
    • 順位を計算する際に、値を丸めるための有効桁数。
    • デフォルト: Inf（丸めない）。数値計算上の微小な誤差によるタイの発生を防ぐために使用されることがあります。

ウィルコクソンの符号順位検定 / Wilcoxon Signed Rank Test

simple_wilcox_signed_rank <- function(x, y = NULL, mu = 0, paired = FALSE,
                                      alternative = "two.sided", exact = NULL, correct = TRUE) {
  # 1. 対応のある検定の場合は差をとる
  if (!is.null(y) && paired) {
    x <- x - y
  }

  # 2. 帰無仮説の期待値(mu)を引いて差を計算し、0を除外する
  x <- x - mu
  x <- x[x != 0]
  n <- length(x)

  # 3. 絶対値で順位付けを行い、正の順位和(V)を求める
  r <- rank(abs(x))
  statistic <- sum(r[x > 0])

  # タイ（同順位）があるかの判定
  ties <- length(r) != length(unique(r))
  if (is.null(exact)) exact <- (n < 50) && !ties

  # 4. p値の計算
  if (exact && !ties) {
    # --- 正確な検定 ---
    p_val <- switch(alternative,
      two.sided = {
        p <- if (statistic > (n * (n + 1) / 4)) {
          psignrank(statistic - 1, n, lower.tail = FALSE)
        } else {
          psignrank(statistic, n)
        }
        min(2 * p, 1)
      },
      greater = psignrank(statistic - 1, n, lower.tail = FALSE),
      less = psignrank(statistic, n)
    )
  } else {
    # --- 正規近似 ---
    nties <- table(r)
    z <- statistic - n * (n + 1) / 4
    # タイを考慮した標準偏差(SIGMA)の計算
    sigma <- sqrt(n * (n + 1) * (2 * n + 1) / 24 - sum(nties^3 - nties) / 48)

    # 連続性の補正
    correction <- 0
    if (correct) {
      correction <- switch(alternative,
        two.sided = sign(z) * 0.5,
        greater = 0.5,
        less = -0.5
      )
    }

    z_stat <- (z - correction) / sigma

    p_val <- switch(alternative,
      less      = pnorm(z_stat),
      greater   = pnorm(z_stat, lower.tail = FALSE),
      two.sided = 2 * min(pnorm(z_stat), pnorm(z_stat, lower.tail = FALSE))
    )
  }

  return(list(statistic = statistic, p.value = p_val))
}

シミュレーションコード

中心が 0 から正の方向にズレた分布からデータを生成し、検定がそのズレ（位置の違い）を正しく検出できるかを確認する、1標本ウィルコクソン符号順位検定のシミュレーション です。

なお、有意水準は5%とします。

# パッケージの読み込み
library(ggplot2)

# 乱数シードの固定
seed <- 20260124
set.seed(seed)

# 1. サンプルデータの生成
# 設定: 真の中心位置は 2.0 である正規分布
# 帰無仮説 (mu = 0) からは明確にズレているデータを作成します
n_sample <- 20
true_mu <- 2.0
sample_data <- rnorm(n_sample, mean = true_mu, sd = 3.0)

# データの可視化
df_one_sample <- data.frame(Value = sample_data)

p1 <- ggplot(df_one_sample, aes(x = Value)) +
  geom_histogram(binwidth = 1, fill = "skyblue", color = "black", alpha = 0.7) +
  geom_vline(aes(xintercept = 0, color = "帰無仮説 (mu=0)"),
    linetype = "dashed", linewidth = 1.2
  ) +
  geom_vline(aes(xintercept = median(sample_data), color = "標本中央値"),
    linewidth = 1.2
  ) +
  scale_color_manual(
    name = "凡例",
    values = c("帰無仮説 (mu=0)" = "red", "標本中央値" = "blue")
  ) +
  labs(
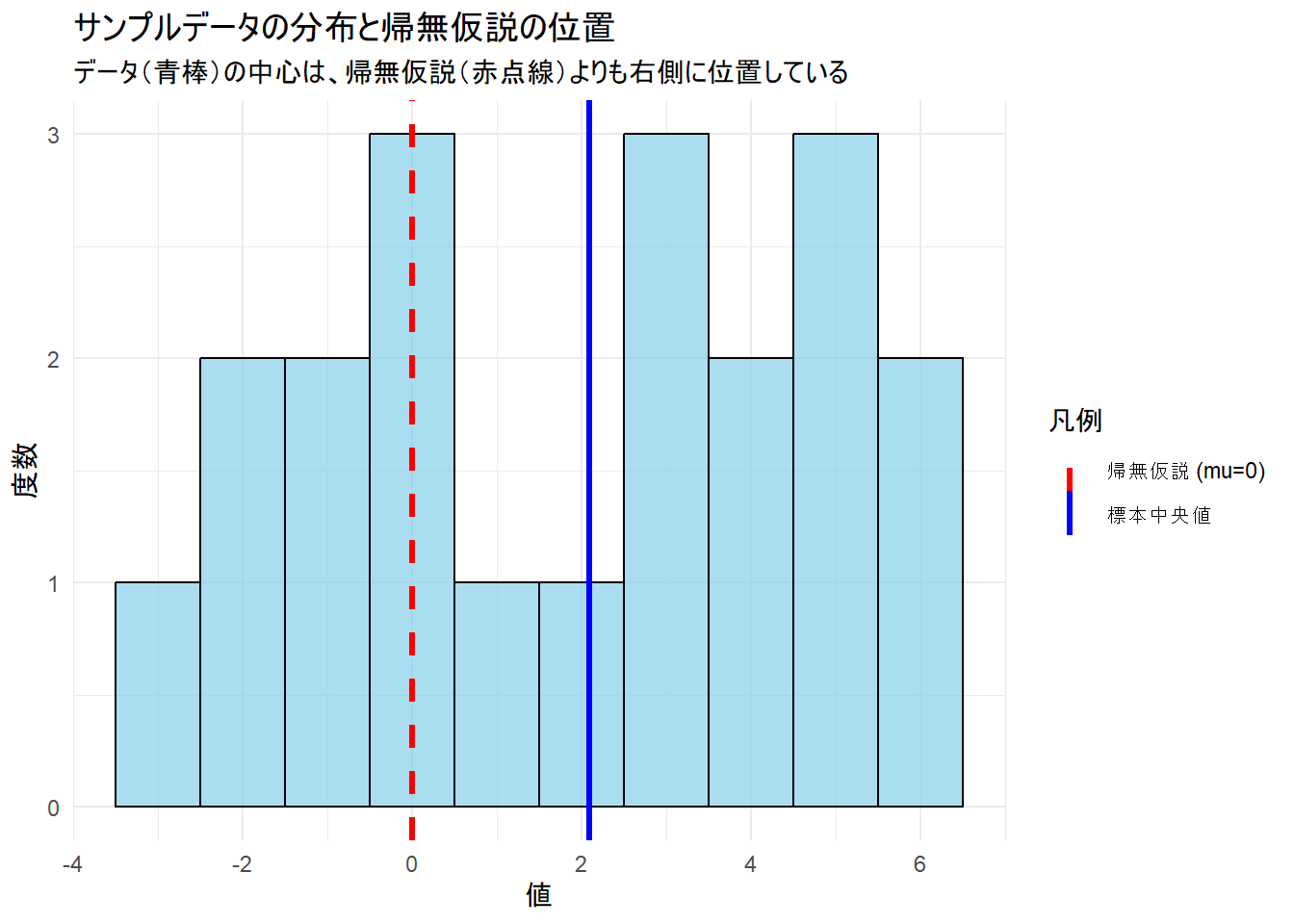
    title = "サンプルデータの分布と帰無仮説の位置",
    subtitle = "データ（青棒）の中心は、帰無仮説（赤点線）よりも右側に位置している",
    x = "値",
    y = "度数"
  ) +
  theme_minimal()

print(p1)

cat("--- データ概要 ---\n")
cat(sprintf("サンプルサイズ: %d\n", n_sample))
cat(sprintf("データの標本中央値: %.3f\n", median(sample_data)))

# 2. 検定の実行
# mu = 0 に対して検定を行います
# conf.int = TRUE で位置の推定値 (pseudo-median) も計算します
test_res <- wilcox.test(sample_data, mu = 0, alternative = "two.sided", conf.int = TRUE)

# 結果の表示
cat("\n\n--- 検定結果 ---\n")
print(test_res)

--- データ概要 ---
サンプルサイズ: 20
データの標本中央値: 2.099


--- 検定結果 ---

    Wilcoxon signed rank exact test

data:  sample_data
V = 165, p-value = 0.02395
alternative hypothesis: true location is not equal to 0
95 percent confidence interval:
 0.3661566 3.2565431
sample estimates:
(pseudo)median 
      1.705651 

simple_wilcox_signed_rank(x = sample_data, mu = 0, alternative = "two.sided")

$statistic
[1] 165

$p.value
[1] 0.02395058