Rの関数から VAR {vars} 引数 season の利用 を確認します。
本ポストはこちらの続きです。

Rの関数:VAR {vars}
const typesetMath = (el) => { if (window.MathJax) { // MathJax Typeset window.MathJax.typeset(); } else if (window.katex...
シミュレーションの設計
- データの構造:
- 四半期データ(1年=4期)を想定し、
season = 4を設定します。
- 四半期データ(1年=4期)を想定し、
- 季節性の導入:
- 変数A (Sales): 第4四半期(年末)に売上が激増する(+10の上乗せ)。
- 変数B (Cost): 第1四半期(年始)にコストが増加する(+5の上乗せ)。
- これに加え、前回同様の「変数間の相互作用(VAR構造)」を持たせます。
- 目的:
- 季節変動があるデータに対し、
season = 4を指定することで、季節性に惑わされずに真の因果関係(ラグ係数)を正しく推定できるかを確認します。
- 季節変動があるデータに対し、
なお、有意水準は5%とします。
Rコード
季節性を持つVARデータの生成
- 観測数: 200 (50年分)
- 季節性: SalesはQ4に急増、CostはQ1に増加するパターンを持つ
# パッケージの読み込み
library(vars)
library(ggplot2)
library(tidyr)
# 乱数シードの固定
seed <- 20260103
set.seed(seed)
# 設定: 2変量VAR(1)モデル + 四半期季節変動
n_years <- 50
n_obs <- n_years * 4 # 200時点 (四半期データ)
# 1. VARの真の係数 (ラグ効果)
# Variable_A(t) = 0.6 * A(t-1) - 0.2 * B(t-1) ...
# Variable_B(t) = 0.3 * A(t-1) + 0.5 * B(t-1) ...
A_true <- matrix(c(0.6, -0.2, 0.3, 0.5), nrow = 2, byrow = TRUE)
# 2. 真の季節効果 (Seasonal Effect)
# 四半期ごとの上乗せ値 (Q1, Q2, Q3, Q4)
# Variable_A: Q4(年末)に +10
season_effect_A <- c(0, 0, 0, 10)
# Variable_B: Q1(年始)に +5
season_effect_B <- c(5, 0, 0, 0)
# データ生成
data_sim <- matrix(0, nrow = n_obs, ncol = 2)
colnames(data_sim) <- c("Sales", "Cost")
# 初期値
y_prev <- matrix(c(0, 0), ncol = 1)
for (t in 1:n_obs) {
# 現在の四半期 (1, 2, 3, 4) を判定
current_q <- (t - 1) %% 4 + 1
# 季節項ベクトル
s_vec <- matrix(c(
season_effect_A[current_q],
season_effect_B[current_q]
), ncol = 1)
# VARプロセス + 季節項 + ノイズ
# y(t) = A * y(t-1) + Season(t) + error
y_curr <- A_true %*% y_prev + s_vec + rnorm(2, sd = 1)
data_sim[t, ] <- as.vector(y_curr)
y_prev <- y_curr # 次のために更新
}
df_sim <- as.data.frame(data_sim)
df_sim$Time <- 1:n_obs
# 可視化用に四半期ラベルを作成
df_sim$Quarter <- factor(paste0("Q", (df_sim$Time - 1) %% 4 + 1))
# データの可視化
p1 <- ggplot(
pivot_longer(df_sim, cols = c("Sales", "Cost"), names_to = "Var"),
aes(x = Time, y = value, color = Var)
) +
geom_line() +
labs(
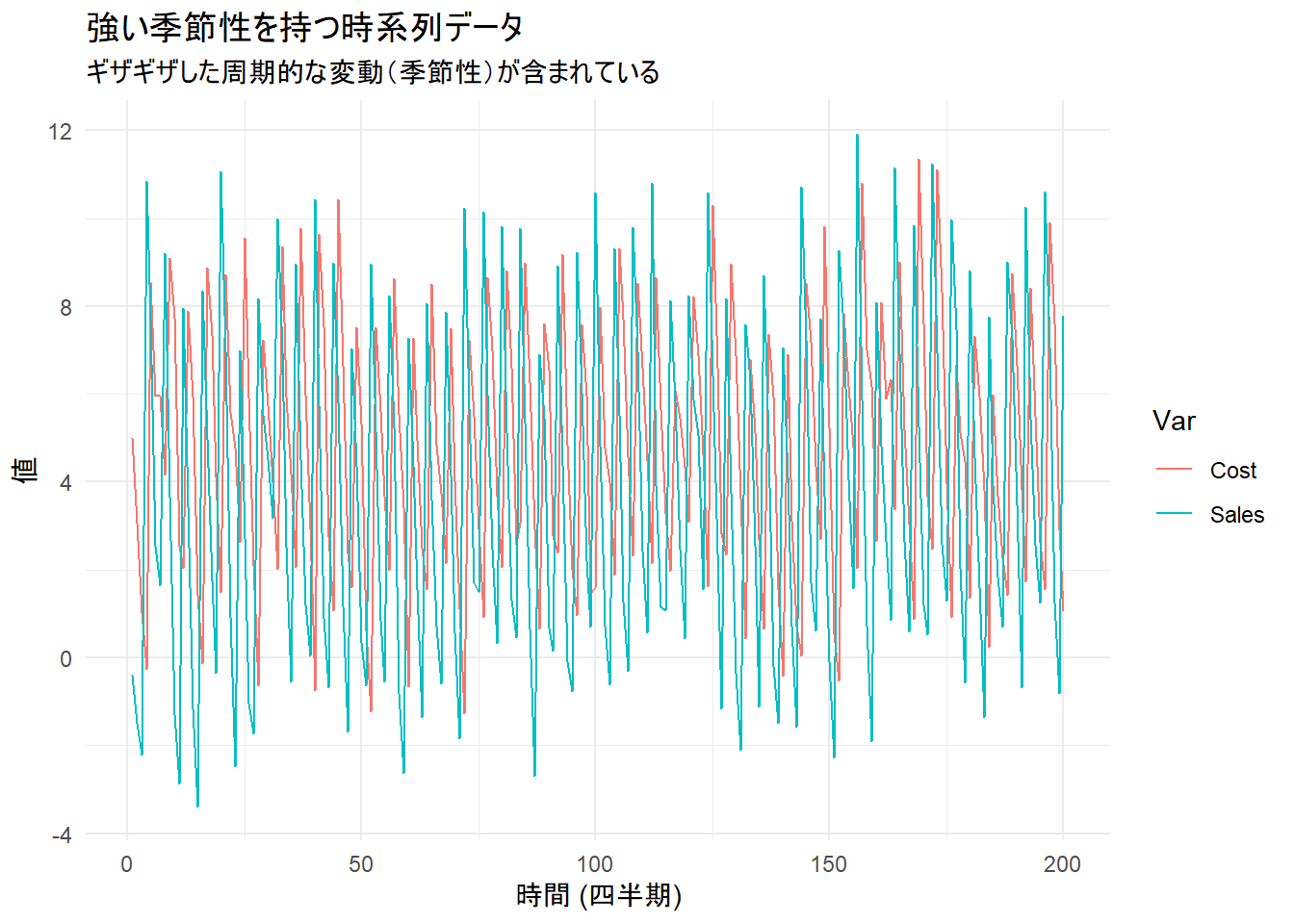
title = "強い季節性を持つ時系列データ",
subtitle = "ギザギザした周期的な変動(季節性)が含まれている",
x = "時間 (四半期)", y = "値"
) +
theme_minimal()
print(p1)VARモデルの推定 (season引数の利用)
# season = 4 を指定して推定
# これにより、季節ダミー変数がモデルに自動追加されます
var_season <- VAR(df_sim[, c("Sales", "Cost")], p = 1, type = "const", season = 4)
print(summary(var_season))
VAR Estimation Results:
=========================
Endogenous variables: Sales, Cost
Deterministic variables: const
Sample size: 199
Log Likelihood: -547.928
Roots of the characteristic polynomial:
0.604 0.604
Call:
VAR(y = df_sim[, c("Sales", "Cost")], p = 1, type = "const",
season = 4L)
Estimation results for equation Sales:
======================================
Sales = Sales.l1 + Cost.l1 + const + sd1 + sd2 + sd3
Estimate Std. Error t value Pr(>|t|)
Sales.l1 0.66812 0.05252 12.720 < 2e-16 ***
Cost.l1 -0.19060 0.05833 -3.267 0.00128 **
const 2.20109 0.30806 7.145 1.8e-11 ***
sd1 -10.50932 0.57949 -18.135 < 2e-16 ***
sd2 -10.60577 0.42331 -25.055 < 2e-16 ***
sd3 -10.32770 0.26031 -39.675 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.004 on 193 degrees of freedom
Multiple R-Squared: 0.9374, Adjusted R-squared: 0.9358
F-statistic: 578.1 on 5 and 193 DF, p-value: < 2.2e-16
Estimation results for equation Cost:
=====================================
Cost = Sales.l1 + Cost.l1 + const + sd1 + sd2 + sd3
Estimate Std. Error t value Pr(>|t|)
Sales.l1 0.32425 0.04944 6.558 4.86e-10 ***
Cost.l1 0.45345 0.05491 8.259 2.30e-14 ***
const 1.36478 0.28998 4.706 4.80e-06 ***
sd1 4.87913 0.54547 8.945 3.05e-16 ***
sd2 0.38403 0.39845 0.964 0.336
sd3 0.03061 0.24503 0.125 0.901
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.9453 on 193 degrees of freedom
Multiple R-Squared: 0.9021, Adjusted R-squared: 0.8996
F-statistic: 355.8 on 5 and 193 DF, p-value: < 2.2e-16
Covariance matrix of residuals:
Sales Cost
Sales 1.00853 -0.05774
Cost -0.05774 0.89359
Correlation matrix of residuals:
Sales Cost
Sales 1.00000 -0.06083
Cost -0.06083 1.00000Sales(売上)の方程式:Q4の急増を制御
シミュレーション設定:
- ラグ効果:
- 前期の自分(
0.6)、前期のコスト(-0.2)
- 前期の自分(
- 季節性:
- Q4(第4四半期)に +10 の加算(Q1~Q3は0)
結果の解釈
-
Sales.l1(0.668) &Cost.l1(-0.191):- 真の値 (
0.6と-0.2) に近い値が推定されており、変数の相互作用を特定できました。
- 真の値 (
- 季節ダミー (
sd1,sd2,sd3):- すべて 約 -10.5 となり、いずれも設定した有意水準を下回っています。
- これは、「Q4(基準となる時期)に比べて、Q1, Q2, Q3 は売上が約10低い」ということを表しています。
- シミュレーションでは「Q4だけ +10」と設定しました。これは相対的に見れば「Q4以外は -10」と同じことです。
Cost(コスト)の方程式:Q1の増加を制御
シミュレーション設定:
- ラグ効果:
- 前期の売上(
0.3)、前期の自分(0.5)
- 前期の売上(
- 季節性:
- Q1(第1四半期)に +5 の加算(他は0)
結果の解釈
-
Sales.l1(0.324) &Cost.l1(0.453):- こちらも真の値 (
0.3と0.5) に近い値が推定されています。
- こちらも真の値 (
- 季節ダミー (
sd1):-
sd1(第1四半期ダミー)のみが 4.879 と設定した有意水準を下回っています。 - これは「Q1 は他の時期より約 5 高い」という設定を正しく捉えた結果です。
-
-
sd2,sd3:- これらは設定した有意水準を上回っています。Q2とQ3には特別な季節性がなく、フラットであるという設定を正しく反映しています。
モデル全体の評価
- 決定係数 (Multiple R-Squared):
- Salesで 0.93、Costで 0.90 と高い値を記録しています。これは、ラグ変数と季節ダミーの組み合わせによって、データの動きの9割以上を説明できていることを意味します。
- 安定性:
-
Roots of the characteristic polynomialが 0.604 であり、1未満であるため、モデルは安定していると考えられます。
-
以上です。