Rの関数から PP.test {stats} を確認します。
関数 PP.test とは
PP.test は、時系列データに対して フィリップス・ペロン検定(Phillips-Perron Unit Root Test) を実行するための関数です。
本検定は、時系列データが 「単位根(Unit Root)」 を持つかどうか、すなわち 「非定常(Non-stationary)」 であるかどうかを判定するために使用されます。
- 帰無仮説 (\(H_0\)):
- データは単位根を持つ(非定常である)。具体的には、ドリフト項を持つランダムウォーク過程に従う。
- 対立仮説 (\(H_1\)):
- データは定常である。具体的には、確定的なトレンド周りで定常(Trend-Stationary)である。
ディッキー・フラー検定(ADF検定)との違い
ADF検定が回帰モデルに「ラグ項(過去の差分)」を追加することで誤差項の自己相関に対処するのに対し、フィリップス・ペロン検定は回帰モデル自体はシンプルに保ちつつ、算出された統計量に対してノンパラメトリックな補正(Newey-Westの推定量を用いた分散の調整)を加えることで、誤差項の自己相関や不均一分散に対処します。
関数 PP.test の引数
args(PP.test)function (x, lshort = TRUE)
NULL-
x- 検定対象となる数値ベクトルまたは単変量時系列オブジェクト。
- ベクトル形式、または列が1つの行列・時系列データである必要があります。多変量データは受け付けません。欠損値(
NA)が含まれている場合、検定前に除外されます。
-
lshort- 誤差項の分散を推定する際に用いる「打ち切りラグ(Truncation lag parameter)」の長さを決定する論理値。
- デフォルト:
TRUE - 検定統計量の補正には、長期分散(Long-run variance)の推定が必要です。この推定には、過去何期分までの自己共分散を考慮するかというパラメータ \(l\) (ラグ)が必要です。
-
TRUEの場合: 短いラグを使用します。計算式は \(l = \text{trunc}(4 \times (n/100)^{0.25})\) です。 -
FALSEの場合: 長いラグを使用します。計算式は \(l = \text{trunc}(12 \times (n/100)^{0.25})\) です。
-
- サンプルサイズ \(n\) に対して、自己相関の影響が短期で消えると考えられる場合は
TRUE、長く残ると考えられる場合はFALSEと使い分けることが出来ます。
シミュレーションコード
以下に、PP.test の機能を確認するためのサンプルデータを用いたシミュレーションコードを示します。
本シミュレーションでは、以下の2つのデータを作成し、検定結果(P値)の違いを確認します。
- 単位根過程(ランダムウォーク): 非定常なデータ。帰無仮説を棄却できないはずです。
- トレンド定常過程: 時間経過とともに上昇するが、その周りでの変動は安定しているデータ。帰無仮説を棄却できるはずです。
また、lshort 引数の違いによる挙動の変化も検証します。
なお、有意水準は5%とします。
サンプルデータの生成
# パッケージの読み込み
library(ggplot2)
library(gridExtra)
# 乱数シードの固定
seed <- 20260222
set.seed(seed)
# ------------------------------------------------------------------------------
# 1. サンプルデータの生成
# ------------------------------------------------------------------------------
n_sample <- 200
time_idx <- 1:n_sample
# シナリオA: 単位根過程 (Random Walk with Drift)
# y_t = c + y_{t-1} + e_t
# 非定常なデータ
rw_drift <- numeric(n_sample)
rw_drift[1] <- 0
for (i in 2:n_sample) {
rw_drift[i] <- 0.5 + rw_drift[i - 1] + rnorm(1)
}
# シナリオB: トレンド定常過程 (Trend Stationary)
# y_t = c + beta * t + e_t
# トレンドを取り除けば定常になるデータ
trend_stationary <- 10 + 0.5 * time_idx + rnorm(n_sample, sd = 5)
# データフレーム化(可視化用)
df_sim <- data.frame(
Time = time_idx,
RandomWalk = rw_drift,
TrendStationary = trend_stationary
)
# データの可視化
p1 <- ggplot(df_sim, aes(x = Time, y = RandomWalk)) +
geom_line(color = "darkred", linewidth = 0.8) +
labs(title = "単位根過程 (非定常)", subtitle = "ランダムウォーク", y = "Value") +
theme_minimal()
p2 <- ggplot(df_sim, aes(x = Time, y = TrendStationary)) +
geom_line(color = "steelblue", linewidth = 0.8) +
labs(title = "トレンド定常過程 (定常)", subtitle = "確定的なトレンド + ノイズ", y = "Value") +
theme_minimal()
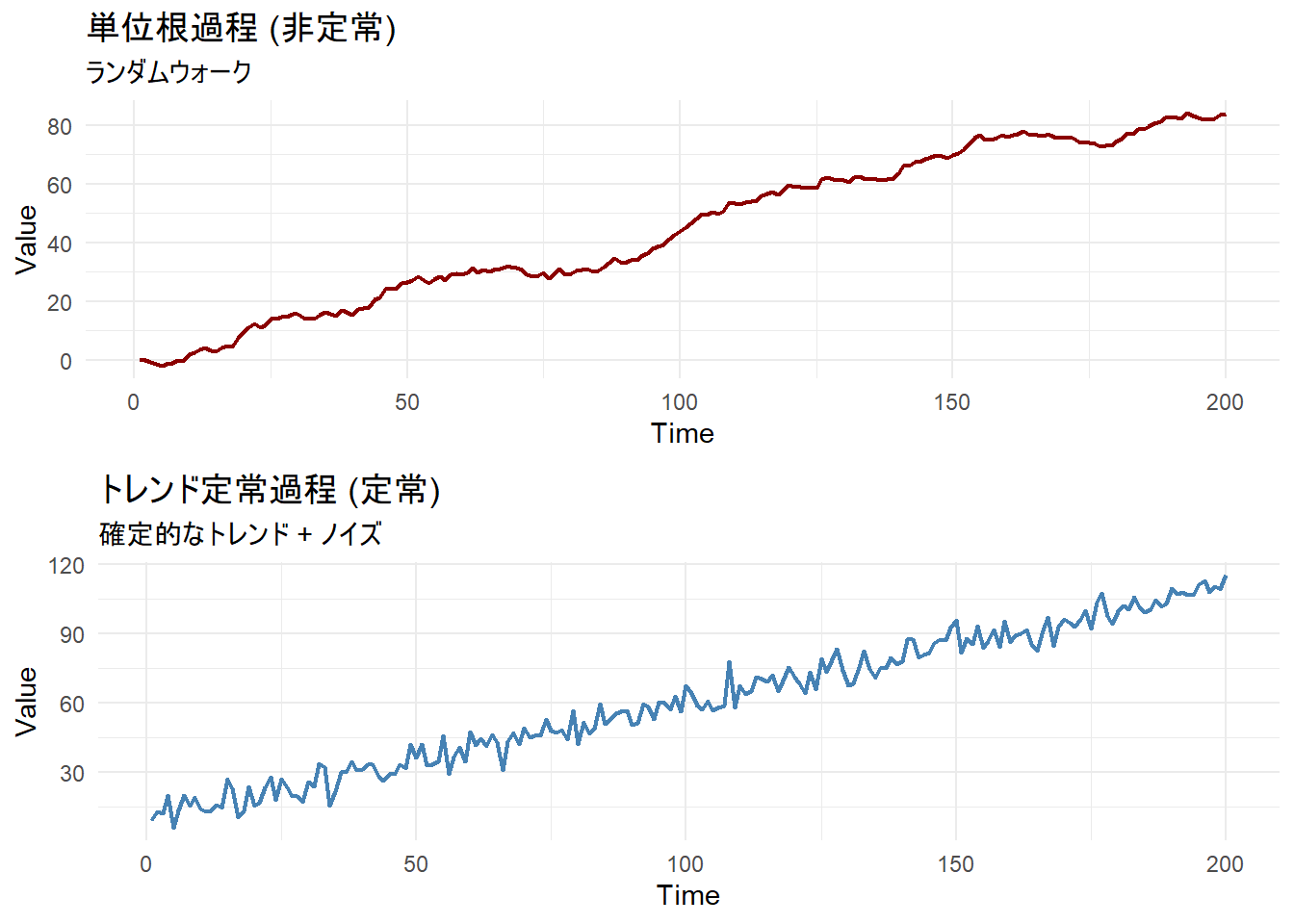
grid.arrange(p1, p2, ncol = 1)Figure 1 のとおり、上図は単位根過程であり、過去の値が蓄積されるため、予測不可能なふらつきを持ち、下図はトレンド定常であり、直線的なトレンドの周りを一定の幅で変動しています。
PP.test の実行と解釈
# ------------------------------------------------------------------------------
# 2. PP.test の実行と解釈
# ------------------------------------------------------------------------------
cat("--- 検定結果の比較 ---\n")
# ケース1: 単位根過程に対する検定
pp_rw <- PP.test(rw_drift)
print(pp_rw)
# ケース2: トレンド定常過程に対する検定
pp_ts <- PP.test(trend_stationary)
print(pp_ts)--- 検定結果の比較 ---
Phillips-Perron Unit Root Test
data: rw_drift
Dickey-Fuller = -1.8175, Truncation lag parameter = 4, p-value = 0.6525
Phillips-Perron Unit Root Test
data: trend_stationary
Dickey-Fuller = -14.559, Truncation lag parameter = 4, p-value = 0.01前提:フィリップス・ペロン検定の仮説
- 帰無仮説 (\(H_0\)): データは単位根を持つ(非定常である)。
- 対立仮説 (\(H_1\)): データは定常である(定常である)。
単位根過程 (pp_rw) の結果
- P値 (p-value): 0.6525
- P値は、設定した有意水準を 超えています。よって、帰無仮説(\(H_0\))「このデータは単位根を持っている(非定常である)」を 棄却できません。シミュレーションで生成した
rw_driftはランダムウォーク(単位根過程)でしたので、正しく検定されています。
- P値は、設定した有意水準を 超えています。よって、帰無仮説(\(H_0\))「このデータは単位根を持っている(非定常である)」を 棄却できません。シミュレーションで生成した
トレンド定常過程 (pp_ts) の結果
- P値 (p-value): 0.01
- P値は、設定した有意水準を 下回っています。よって、帰無仮説(\(H_0\))は 棄却され、対立仮説(\(H_1\))「このデータは定常である」が採択されます。シミュレーションで生成した
trend_stationaryは、トレンドを除けば安定した定常過程でしたので、正しく検定されています。
- P値は、設定した有意水準を 下回っています。よって、帰無仮説(\(H_0\))は 棄却され、対立仮説(\(H_1\))「このデータは定常である」が採択されます。シミュレーションで生成した
共通事項:ラグパラメータについて
- Truncation lag parameter = 4
- 両方の結果でラグパラメータは
4になっています。これは引数lshort = TRUE(デフォルト)が機能した結果です。 - サンプルサイズ \(n=200\) に対して、計算式 \(\text{trunc}(4 \times (200/100)^{0.25}) \approx \text{trunc}(4 \times 1.189) = 4\) が適用され、過去4期分までの自己相関構造を考慮して補正が行われたことを示しています。
- 両方の結果でラグパラメータは
引数 lshort の違いによる挙動の確認
同じデータ(単位根過程)に対して、ラグパラメータを変えて検定します。
# ------------------------------------------------------------------------------
# 3. 引数 lshort の違いによる挙動の確認
# ------------------------------------------------------------------------------
cat("--- 引数 lshort (TRUE vs FALSE) の比較 ---\n")
# lshort = TRUE (デフォルト: 短いラグ)
pp_short <- PP.test(rw_drift, lshort = TRUE)
# lshort = FALSE (長いラグ)
pp_long <- PP.test(rw_drift, lshort = FALSE)
# 結果の比較表示
df_lshort <- data.frame(
Setting = c("lshort = TRUE", "lshort = FALSE"),
Lag_Parameter = c(pp_short$parameter, pp_long$parameter),
Statistic = c(pp_short$statistic, pp_long$statistic),
P_Value = c(pp_short$p.value, pp_long$p.value)
)
print(df_lshort)--- 引数 lshort (TRUE vs FALSE) の比較 ---
Setting Lag_Parameter Statistic P_Value
1 lshort = TRUE 4 -1.817468 0.6525418
2 lshort = FALSE 14 -2.135515 0.5193424ラグパラメータ(Lag Parameter)の違い
- lshort = TRUE: ラグは 4
- lshort = FALSE: ラグは 14
lshort = FALSE(ロング・ラグ)を指定すると、TRUE の場合の約3倍の期間(過去14時点分)の自己相関を考慮して、誤差項の長期分散を推定します。
統計量とP値の変化
ラグを長く取ったことで、統計量の補正計算に用いられる項が変化し、結果として数値が変動しています。
- Statistic: -1.81 \(\to\) -2.13 (より負の方向に動いた)
- P_Value: 0.65 \(\to\) 0.51 (やや小さくなった)
過去の情報を多く取り込んだ結果、統計量は「単位根がない(定常)」という方向に傾きましたが、本例では結論に違いは生じません。
関数 PP.test のコード
PP.test_commented <- function(x, lshort = TRUE) {
# --- 1. 入力チェック ---
# 単変量データであることを確認します。
if (NCOL(x) > 1) {
stop("x is not a vector or univariate time series")
}
DNAME <- deparse1(substitute(x)) # データ名を保存
# --- 2. データの準備 (ラグデータの作成) ---
# embed関数を使って、現在の値(yt)と1期前の値(yt1)のペアを作ります。
# x = (x1, x2, ..., xn)
# z[,1] = (x2, x3, ..., xn) -> yt
# z[,2] = (x1, x2, ..., xn-1) -> yt1
z <- embed(x, 2)
yt <- z[, 1]
yt1 <- z[, 2]
n <- length(yt) # 有効サンプルサイズ (元の長さ - 1)
# --- 3. 基礎となる回帰分析 (OLS) ---
# 時間トレンド項 u を作成 (中心化した時間)
u <- (1L:n) - n / 2
# 線形回帰モデル: y_t = alpha + beta * t + rho * y_{t-1} + e_t
# ここでの係数 rho (yt1の係数) が 1 かどうかを検定します。
res <- lm(yt ~ 1 + u + yt1)
if (res$rank < 3) {
stop("singularities in regression")
} # 共線性などで計算不能な場合
# --- 4. ディッキー・フラー統計量の計算 ---
# 回帰係数と標準誤差を取得
cf <- coef(summary(res))
# yt1の係数 (cf[3, 1]) に対するt統計量を計算
# 帰無仮説は係数 = 1 なので、(係数 - 1) / 標準誤差
# これが通常のt値ですが、PP検定ではこれを後で補正します。
tstat <- (cf[3, 1] - 1) / cf[3, 2]
# 残差 u の取得
u <- residuals(res)
# 残差の分散 (単純な分散)
ssqru <- sum(u^2) / n
# --- 5. Newey-West 推定量による長期分散の推定 ---
# 打ち切りラグパラメータ l の決定
# lshort=TRUE なら 4*(n/100)^0.25, FALSE なら 12*(n/100)^0.25
l <- if (lshort) {
trunc(4 * (n / 100)^0.25)
} else {
trunc(12 * (n / 100)^0.25)
}
# C言語の関数 .Call(C_pp_sum, u, l) を呼び出して、
# 重み付き自己共分散の和を計算しています。
# ssqrtl は「長期分散 (long-run variance)」の推定値です。
ssqrtl <- ssqru + .Call(stats:::C_pp_sum, u, l)
# --- 6. 統計量の補正 (Phillips-Perron Z統計量の導出) ---
# ここからの計算は、通常のt統計量(tstat)を、誤差項の自己相関や
# 不均一分散を考慮して修正するための数式です。
n2 <- n^2
# 補正項の計算に必要な要素 (回帰行列の行列式に関連する項など)
trm1 <- n2 * (n2 - 1) * sum(yt1^2) / 12
trm2 <- n * sum(yt1 * (1L:n))^2
trm3 <- n * (n + 1) * sum(yt1 * (1L:n)) * sum(yt1)
trm4 <- (n * (n + 1) * (2 * n + 1) * sum(yt1)^2) / 6
Dx <- trm1 - trm2 + trm3 - trm4 # 行列式に相当する値
# 統計量 STAT (Z_t) の計算
# 第1項: tstat * (単純分散 / 長期分散)^(1/2) -> 分散の違いでスケーリング
# 第2項: 自己相関によるバイアスを差し引く補正項
STAT <- sqrt(ssqru) / sqrt(ssqrtl) * tstat - (n^3) / (4 * sqrt(3) *
sqrt(Dx) * sqrt(ssqrtl)) * (ssqrtl - ssqru)
# --- 7. P値の計算 ---
# ディッキー・フラー分布の近似表
# このテーブルは有限サンプルでのクリティカル値を補間するために使われます。
table <- cbind(c(4.38, 4.15, 4.04, 3.99, 3.98, 3.96), c(
3.95,
3.8, 3.73, 3.69, 3.68, 3.66
), c(
3.6, 3.5, 3.45, 3.43,
3.42, 3.41
), c(3.24, 3.18, 3.15, 3.13, 3.13, 3.12), c(
1.14,
1.19, 1.22, 1.23, 1.24, 1.25
), c(
0.8, 0.87, 0.9, 0.92,
0.93, 0.94
), c(0.5, 0.58, 0.62, 0.64, 0.65, 0.66), c(
0.15,
0.24, 0.28, 0.31, 0.32, 0.33
))
table <- -table # 統計量は負の値をとるため符号反転
tablen <- dim(table)[2L]
tableT <- c(25, 50, 100, 250, 500, 1e+05) # サンプルサイズの基準点
tablep <- c(0.01, 0.025, 0.05, 0.1, 0.9, 0.95, 0.975, 0.99) # 確率の基準点
# 現在のサンプルサイズ n に合わせてクリティカル値を補間
tableipl <- numeric(tablen)
for (i in (1L:tablen)) {
tableipl[i] <- approx(tableT, table[
,
i
], n, rule = 2)$y
}
# 計算された統計量 STAT に対応する P値を補間
PVAL <- approx(tableipl, tablep, STAT, rule = 2)$y
# --- 8. 結果の出力 ---
PARAMETER <- l
METHOD <- "Phillips-Perron Unit Root Test"
names(STAT) <- "Dickey-Fuller"
names(PARAMETER) <- "Truncation lag parameter"
structure(list(
statistic = STAT, parameter = PARAMETER, p.value = PVAL,
method = METHOD, data.name = DNAME
), class = "htest")
}以上です。