Rの関数:mmkh {modifiedmk}

Rの関数から mmkh {modifiedmk} を確認します。

関数 `mmkh` とは

mmkh は、時系列データのトレンド検定において、データの自己相関（Autocorrelation）の影響を補正した修正マン・ケンドール検定（Modified Mann-Kendall Test） を実行する関数です。

通常のマン・ケンドール検定は、データが互いに独立であることを仮定しています。

しかし、河川流量や気温などの環境データには、過去の値が現在の値に影響を与える「自己相関」が含まれることが一般的です。

正の自己相関が存在する場合、通常の検定では分散が過小評価され、実際にはトレンドがないにもかかわらず「有意なトレンドがある」と誤って判定（第一種の過誤）してしまうリスクが高まります。

mmkh は、まずデータのトレンドを除去し、その残差のランク（順位）に基づいて有効な自己相関係数を計算します。

その結果を用いてマン・ケンドール統計量 \(S\) の分散を膨らませる（補正する）ことで、自己相関の影響を相殺し、より堅牢な検定結果を提供します。

関数 `mmkh` の引数

library(modifiedmk)
args(mmkh)

function (x, ci = 0.95) 
NULL

x
- 検定対象となる数値ベクトルです。時系列データを指定します。
- ベクトル形式であり、有限の数値（NAやInfを含まない）である必要があります。また、内部処理でトレンド除去を行うため、少なくとも3つの要素が必要です。
ci
- 自己相関係数の有意性を判定するための信頼水準（Confidence Interval）です。
- デフォルト: 0.95（95%信頼区間）。

返り値（出力）の主要な要素

関数は以下の要素を含む名前付きベクトルを返します。

Corrected Zc:
- 自己相関を補正した後の検定統計量 \(Z\)。
new P-value:
- 補正後の \(Z\) に基づくP値。最終的な判断にはこの値を用います。
N/N*:
- 分散補正係数（有効サンプルサイズの比率）。値が大きいほど自己相関の影響が強いことを示します。
Original Z:
- 補正前の通常のマン・ケンドール検定統計量。
old P.value:
- 補正前のP値。
Sen's slope:
- センの傾き（トレンドの勾配推定値）。

シミュレーションコード

以下に、mmkh の機能を確認するためのシミュレーションコードを示します。

このシミュレーションでは、「トレンドはないが、強い自己相関を持つデータ（ARモデル）」 を生成します。

このようなデータに対して、通常の検定（補正なし）と mmkh（補正あり）を適用し、結果がどのように異なるかを確認します。

予想される結果:
- 通常の検定（old P.value）は、自己相関をトレンドと誤解し、誤って「有意」と判定してしまう可能性があります。
- 修正検定（new P-value）は、自己相関を考慮して分散を補正するため、「有意ではない（トレンドなし）」と正しく判定することが期待されます。

なお、有意水準は5%とします。

シミュレーションデータの生成

トレンド項は含まないが、強い自己相関 (AR=0.8) を持つ、一見するとトレンドがあるように見えやすいデータを生成します。

# パッケージの読み込み
library(ggplot2)

# 乱数シードの固定
seed <- 20251228
set.seed(seed)

# 設定: 期間100の時系列データ
n <- 100
time_index <- 1:n

# データの生成: トレンド無しだが、強い自己相関を持つAR(1)プロセス
# y_t = 0.8 * y_{t-1} + error
# 係数 0.8 は、前の値の影響を強く受けることを意味します
x_autocorr <- arima.sim(model = list(ar = 0.8), n = n)

# データフレーム化
df_sim <- data.frame(
  Time = time_index,
  Value = as.numeric(x_autocorr)
)

# データの可視化
p1 <- ggplot(df_sim, aes(x = Time, y = Value)) +
  geom_line(color = "steelblue", linewidth = 1) +
  geom_smooth(method = "lm", color = "red", linetype = "dashed", se = FALSE) +
  labs(
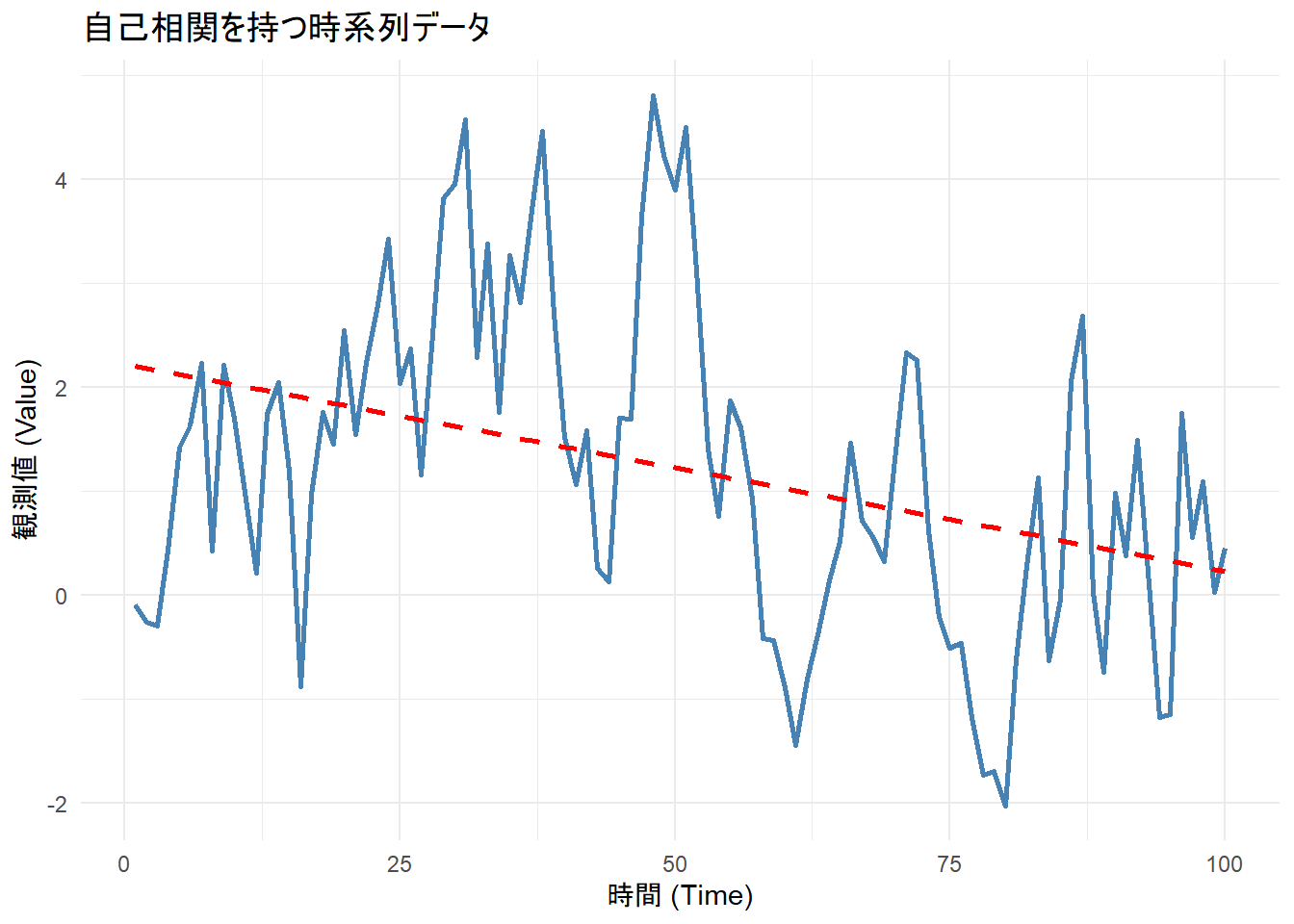
    title = "自己相関を持つ時系列データ",
    x = "時間 (Time)",
    y = "観測値 (Value)"
  ) +
  theme_minimal()

print(p1)

Figure 1 から、真のトレンドはゼロですが、自己相関により局所的な上昇・下降が長く続く様子が確認できます。

mmkh による検定の実行

# 関数 mmkh を適用
res_mmkh <- mmkh(df_sim$Value, ci = 0.95)

cat("--- 関数 mmkh による検定結果---\n")
print(stack(res_mmkh))

--- 関数 mmkh による検定結果---
             values          ind
1     -1.7577310977 Corrected Zc
2      0.0787932739  new P-value
3      3.8827372858         N/N*
4     -3.4635498240   Original Z
5      0.0005330979  old P.value
6     -0.2351515152          Tau
7     -0.0187153760  Sen's slope
8 112750.0000000000 old.variance
9 437778.6289767753 new.variance

補正なし（Original）の結果

まず、通常のマン・ケンドール検定に相当する結果を見てみましょう。

Original Z: -3.46
old P.value: 0.00053

p値が設定した有意水準を下回っているため、もしこの結果をそのまま信じると、「統計的に有意なトレンドが存在する」という誤った結論を下してしまいます。

これは、強い自己相関によってデータが一定期間低い値をとり続けた現象を、検定が「トレンドによる減少」と誤解したために起こりました。

補正あり（Corrected）の結果

次に、補正された結果を見てみましょう。

Corrected Zc: -1.76
new P-value: 0.0788

p値が設定した有意水準を上回りました。

それゆえ、「統計的に有意なトレンドは無い」 との帰無仮説は棄却できません。

分散と補正係数

N/N* (補正係数): 3.88
old.variance: 112,750
new.variance: 437,779 （約 3.88倍に増加）

mmkh 関数は、データの自己相関を分析し、「データ同士が似通っている（相関している）ため、実質的な情報量は見た目のサンプルサイズの約 1/3.88 しかない」と判断しました。

その結果、統計量の分散（不確実性の幅）を約4倍に膨らませました。

分散が大きくなると検定の基準が厳しくなるため、補正前は「有意（-3.46）」に見えたZ値も、厳しい基準に照らせば「誤差の範囲内（-1.76）」へと引き下げられたのです。

以上です。

関数 mmkh とは

関数 mmkh の引数